Hoy hablaré sobre tres algoritmos que tienen una alta frecuencia y son fáciles de confundir: subconjunto, permutación y combinación. Estos problemas se pueden resolver con el algoritmo de retroceso.
1. El
problema del subconjunto es muy simple: ingrese una matriz que no contenga números duplicados y solicite al algoritmo que muestre todos los subconjuntos de estos números.
vector <vector < int >> subconjuntos (vector < int > & nums);
Por ejemplo, ingresando nums = [1,2,3], su algoritmo debe generar 8 subconjuntos, incluido el conjunto vacío y él mismo, el orden puede ser diferente:
[[], [1], [2], [3], [1,3], [2,3], [1,2], [1,2,3]]
La primera solución es utilizar la idea de la inducción matemática: supongamos que ahora conozco los resultados de un subproblema más pequeño, ¿cómo puedo obtener los resultados del problema actual?
Específicamente, déjame preguntarte por el subconjunto de [1,2,3]. Si conoces el subconjunto de [1,2], ¿puedes derivar el subconjunto de [1,2,3]? Primero escriba el subconjunto de [1,2] y eche un vistazo:
[[], [1], [2], [1,2]]
Encontrará tal regla:
subconjunto ([1,2,3]) - subconjunto ([1,2])
= [3], [1,3], [2,3], [1,2,3]
Y este resultado es agregar 3 a cada conjunto en el resultado de sebset ([1,2]).
En otras palabras, si A = subconjunto ([1,2]), entonces:
subconjunto ([1,2,3])
= A + [A [i] .add (3) para i = 1..len (A)]
Esta es una estructura recursiva típica: el subconjunto de [1,2,3] puede agregarse por [1,2], el subconjunto de [1,2] puede agregarse por [1], el caso base es obviamente Es decir, cuando el conjunto de entrada es un conjunto vacío, el subconjunto de salida también es un conjunto vacío.
Traducido al código, es fácil de entender:
vector <vector < int >> subconjuntos (vector < int > & nums) { // caso base, devuelve un conjunto vacío if (nums.empty ()) return {{}}; // saca el último elemento int n = nums.back (); nums.pop_back (); // Calcular recursivamente todos los subconjuntos de los elementos anteriores vector <vector < int >> res = subsets (nums); int size = res.size (); for ( int i = 0 ; i <size; i ++ ) { // Luego agregue res.push_back (res [i]); res.back (). push_back (n); } returnres; }
El cálculo de la complejidad temporal de este problema es relativamente fácil. El método que usamos para calcular la complejidad temporal del algoritmo recursivo es encontrar la profundidad de la recursión y luego multiplicarla por el número de iteraciones en cada recursión. Para este problema, la profundidad de recursión es obviamente N, pero descubrimos que el número de iteraciones de cada bucle recursivo depende de la longitud de res y no es fijo.
Según la idea de ahora, la duración de la resolución debería duplicar cada recursión, por lo que el número total de iteraciones debería ser 2 ^ N. O sin tanta molestia, ¿cuántos subconjuntos de un conjunto de tamaño N crees? 2 ^ N a la derecha, así que al menos agrega 2 ^ N elementos a res.
Entonces, ¿es la complejidad temporal del algoritmo O (2 ^ N)? Todavía no es correcto, los subconjuntos 2 ^ N se agregan mediante push_back a res, por lo que se debe considerar la eficiencia de la operación push_back:
vector <vector < int >> res = ... para ( int i = 0 ; i <tamaño; i ++ ) { res.push_back (res [i]); // O (N) res.back (). Push_back (n); // O (1) }
Como res [i] también es una matriz, push_back copia una copia de res [i] y la agrega al final de la matriz, por lo que el tiempo para una operación es O (N).
En resumen, la complejidad del tiempo total es O (N * 2 ^ N), lo que consume bastante tiempo.
Para la complejidad del espacio, si no calcula el espacio utilizado para almacenar el resultado devuelto, solo se requiere un espacio de pila recursivo O (N). Si se calcula el espacio requerido para res, debe ser O (N * 2 ^ N).
El segundo método general es el algoritmo de retroceso. El antiguo algoritmo de retroceso de texto explicaba en detalle la plantilla del algoritmo de retroceso:
result = [] def backtrack (ruta, lista de selección): si se cumple la condición final: result.add (ruta) regresar para la selección en la lista de selección: hacer la selección backtrack (ruta, lista de selección) para cancelar la selección
Simplemente modifique la plantilla del algoritmo de retroceso:
vector <vector < int >> res; vector <vector < int >> subconjuntos (vector < int > & nums) { // Registre la ruta recorrida vector < int > track; backtrack (nums, 0 , track); return res ; } void backtrack (vector < int > & nums, int start, vector < int > & track) { res.push_back (track); // Tenga en cuenta que i incrementa desde el inicio para ( int i = start; i <nums.size (); i ++ ) { // hacer una elección track.push_back (nums [i]); // backtracking backtrack (nums, i + 1 , track); // deseleccionar la selección track.pop_back (); } }
Como puede ver, la actualización de res es un recorrido previo al pedido, es decir, res es todos los nodos del árbol:

2. Combine
dos números n, k, y el algoritmo genera todas las combinaciones de k números en [1..n].
vector <vector <int >> combine (int n, int k); Por
ejemplo, ingresando n = 4, k = 2, generando los siguientes resultados, el orden no importa, pero no puede contener repetición (de acuerdo con la definición de combinación, [1,2] y [ 2,1] también se repite):
[
[1,2],
[1,3],
[1,4],
[2,3],
[2,4],
[3,4]
]
Este es un algoritmo de retroceso típico. K limita la altura del árbol yn limita el ancho del árbol. Simplemente aplique el marco de plantilla del algoritmo de retroceso del que hablamos antes:
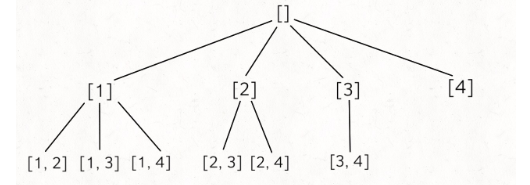
vector <vector < int >> res; vector <vector < int >> combine ( int n, int k) { if (k <= 0 || n <= 0 ) return res; vector < int > pista; retroceso (n, k, 1 , seguimiento); volver res; } retroceso vacío ( int n, int k, int start, vector < int > & track) { // 到达 树 的 底部 if (k ==track.size ()) { res.push_back (track); return ; } // Tenga en cuenta que i aumenta desde el inicio para ( int i = start; i <= n; i ++ ) { // tome las decisiones track.push_back (i) ; BackTrack (n-, K, I + 1. , Track); // deselección track.pop_back (); } }
La función de retroceso es similar al subconjunto de cálculo, la diferencia es que el lugar para actualizar res es la parte inferior del árbol.
3. Permutación
Ingrese una matriz de números que no contenga números duplicados y devuelva todas las permutaciones de estos números.
vector <vector <int >> permute (vector <int> & nums);
Por ejemplo, la matriz de entrada [1,2,3], el resultado de salida debe ser el siguiente, el orden no importa, no puede haber repetición:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
En la explicación detallada del algoritmo de retroceso, este problema se utiliza para explicar la plantilla de retroceso. Este problema también se enumera aquí, que consiste en comparar los códigos de los dos algoritmos de retroceso de "disposición" y "combinación".
Primero dibuje un árbol de rastreo para echar un vistazo:
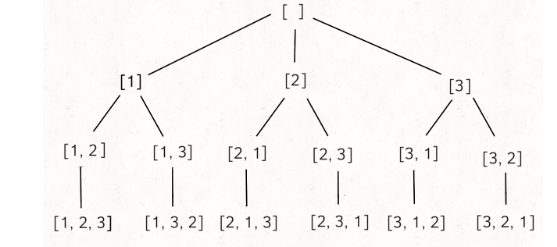
Utilizamos código Java para escribir la solución:
List <List <Integer >> res = new LinkedList <> (); / * Función principal, ingresa un grupo de números que no se repiten y devuelve su disposición completa * / List <List <Integer >> permute ( int [] nums) { // Grabe la "ruta" LinkedList <Integer> track = new LinkedList <> (); backtrack (nums, track); return res; } void backtrack ( int [] nums, LinkedList <Integer> track) { // Fin del disparador Condicional if (track.size () == nums.length) { res.add ( new LinkedList (track)); return ; } para( int i = 0 ; i <nums.length; i ++ ) { // Excluir opciones ilegales if (track.contains (nums [i])) continuar ; // Hacer elecciones track.add (nums [i]); // Ingrese el siguiente nivel de retroceso del árbol de decisión (nums, track); // Deseleccione track.removeLast (); } }
La plantilla de retroceso no ha cambiado, pero de acuerdo con el árbol dibujado por el problema de permutación y el problema de combinación, el árbol del problema de permutación es más simétrico y cuanto más cerca esté el árbol del problema de combinación, menores serán los nodos correctos.
La manifestación en el código es que el problema de disposición usa el método contiene para excluir los números que se han seleccionado en la pista cada vez; y el problema de combinación pasa en un parámetro de inicio para excluir el número antes del índice de inicio.
Lo anterior es la solución a los tres problemas de permutación, combinación y subconjunto.
El problema del subconjunto puede utilizar la idea de inducción matemática, suponiendo que se conocen los resultados de un problema menor y cómo derivar los resultados del problema original. También puede usar un algoritmo de retroceso, usando el parámetro de inicio para excluir los números seleccionados.
El problema de combinación usa la idea de retroceso, y el resultado puede expresarse como una estructura de árbol. Solo necesitamos aplicar la plantilla del algoritmo de retroceso. El punto clave es usar un inicio para excluir los números que han sido seleccionados.
El problema de la disposición es una idea retrospectiva, y también se puede expresar como una estructura de árbol para aplicar la plantilla del algoritmo. El punto clave es utilizar el método contiene para excluir los números seleccionados. El artículo anterior tiene un análisis detallado. Aquí, se compara principalmente con el problema de combinación.
Para estos tres problemas, puede comprender el significado del código observando la estructura del árbol recursivo. .