[ML-13-1 ] Modelo oculto de Markov HMM
[ML-13-2 ] Modelo oculto de Markov HMM- algoritmo hacia adelante y hacia atrás
[ML-13-3 ] Modelo oculto de Markov HMM - Baum-Welch ( Baum- Welch)
[ML-13-4 ] Modelo de Markov oculto HMM-- Algoritmo de Viterbi (Viterbi) para problemas de predicción
Directorio
- Conceptos básicos: cálculo de la probabilidad común de HMM
- HMM algoritmo de aproximación de secuencia de estado oculto más probable
- Algoritmo de Viterbi
- Ejemplos de algoritmo de Viterbi
Solución al último problema del modelo HMM: encuentre la secuencia de estado oculta correspondiente que es más probable que ocurra bajo la secuencia de observación dada. Es decir, dado el modelo λ = (A, B, π) y la secuencia de observación Q = {q1, q2, ..., qT}, encuentre el estado oculto con la mayor probabilidad condicional P (I | Q, λ) de la secuencia de observación dada secuenciar la I. Antes de leer este artículo, se recomienda leer el primer artículo de esta serie para familiarizarse con el modelo HMM.
El algoritmo más utilizado para el problema de decodificación del modelo HMM es el algoritmo de Viterbi. Por supuesto, hay otros algoritmos que pueden resolver este problema. Al mismo tiempo, el algoritmo de Viterbi es un algoritmo general de programación dinámica para encontrar la ruta más corta en la secuencia. También se puede utilizar para muchos otros problemas, como el principio de segmentación de palabras de la minería de textos.
Este artículo se centra en la secuencia de estado oculta más probable de la decodificación HMM con el algoritmo Viterbi.
1. Cálculo básico de la probabilidad común de HMM
Usando las probabilidades hacia adelante y hacia atrás, podemos calcular la fórmula de probabilidad para un solo estado y dos estados en el HMM.
1.1 Probabilidad de un solo estado
Dado el modelo λ y la secuencia de observación Q, la probabilidad de estar en el estado si en el tiempo t se escribe como:
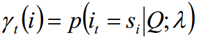
La importancia de la probabilidad de un solo estado se usa principalmente para juzgar el estado más probable en cada momento, de modo que se pueda obtener una secuencia de estado como resultado final de la predicción.
Usando la definición de probabilidad hacia adelante y hacia atrás, podemos saber:
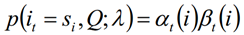
De las dos expresiones anteriores:

1.2 Probabilidad conjunta de dos estados
Dado el modelo λ y la secuencia de observación Q, la probabilidad de estar en el estado si en el tiempo t y estar en el estado sj en el tiempo t + 1 se escribe como:
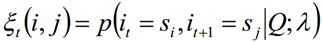
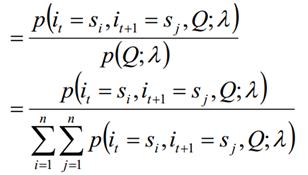
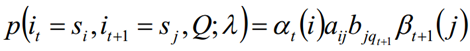
1.3 Se pueden obtener las dos sumas anteriores:
2. HMM algoritmo de aproximación de secuencia de estado oculto más probable
En el problema de decodificación del modelo HMM, dado el modelo λ = (A, B, Π) y la secuencia de observación, encuentre la secuencia de estado correspondiente más probable I = {i1, i2, .. .iT}, es decir, P (I | Q) debe maximizarse. El mejor estado posible directamente en cada momento t se usa como el estado final predicho, y el valor de probabilidad se calcula usando la siguiente fórmula:

Solo necesita satisfacer el valor que maximiza la probabilidad de la fórmula anterior, que puede obtenerse hacia adelante y hacia atrás.
El algoritmo de aproximación es muy simple, pero no puede garantizar que la secuencia de estado predicha sea la secuencia de estado más probable en su conjunto, porque algunos estados ocultos adyacentes en la secuencia de estado predicha pueden tener una probabilidad de transición de 0.
El algoritmo de Viterbi puede considerar la secuencia de estado de HMM como un todo para evitar el problema de los algoritmos de aproximación. Veamos el algoritmo de Viterbi para la decodificación de HMM.
Tres, algoritmo de Viterbi (Viterbi)
El algoritmo de Viterbi en realidad resuelve el problema de predicción HMM con la idea de la programación dinámica, y encuentra el "camino" con la mayor probabilidad. Cada "camino" corresponde a una secuencia de estado:
En el tiempo t, el estado oculto es la probabilidad máxima de todas las posibles rutas de transición de estado i1, i2, ... it. Registrado como δt (i):
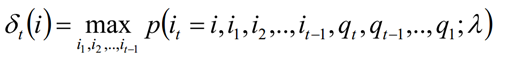
La expresión recursiva de δ se puede obtener de la definición de δt (i):
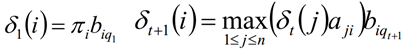
Calcule el δT (i) máximo en el tiempo T, que es la probabilidad de la secuencia de estado oculta más probable.
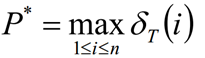
Después de hacer que la fórmula anterior sea máxima, la secuencia de estado oculta más probable es I ∗ = {i ∗ 1, i ∗ 2, ... i ∗ T}
Cuatro ejemplos de algoritmos de Viterbi (Viterbi)
4.1 Ejemplos
Supongamos que hay tres cajas, numeradas 1,2,3; cada caja está equipada con pequeñas bolas de colores blanco y negro, la proporción de las bolas es la siguiente:
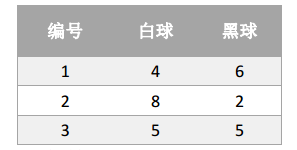
De acuerdo con las siguientes reglas, la bola con el reemplazo se extrae para obtener la secuencia de observación del color de la bola:
- Seleccione un cuadro de acuerdo con la probabilidad de π, extraiga aleatoriamente una pequeña bola del cuadro, registre el color y vuelva a colocarlo en el cuadro;
- Seleccione un nuevo cuadro de acuerdo con una cierta probabilidad condicional y repita la operación;
- Obtuve la secuencia de observación finalmente: "Blanco negro y blanco blanco negro
- Conjunto de estados: S = {Cuadro 1, Cuadro 2, Cuadro 3}
- Conjunto de observación: O = {blanco, negro}
- Secuencia de estado y longitud de secuencia de observación T = 5
- Distribución de probabilidad inicial π
- Matriz de probabilidad de transición de estado A
- Matriz de probabilidad de observación B

Cuando se dan los parámetros π, A y B, la secuencia de observación es "blanca, negra, blanca, blanca y negra", y se obtiene la secuencia óptima de estado oculto.
4.2 Proceso de cálculo
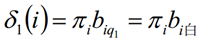
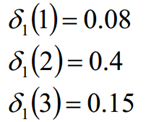


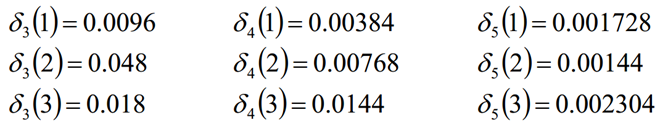
La secuencia final de la caja es: (2, 3, 2, 2, 3)
Apéndice 1: ejercicios de escritura a mano



