Article Directory
- Why use homogeneous coordinates
This article numbers issued to the public: Computer Vision life.
Original link: to learn from scratch with SLAM | Why use homogeneous coordinates?
Why use homogeneous coordinates
In geometry problems related to computer vision, we often see the term homogeneous coordinates. This article explain exactly why to use homogeneous coordinates? Use homogeneous coordinates in the end what are the benefits?
What is the homogeneous coordinates?
Simply put: homogeneous coordinates is to add a dimension in the original coordinates:
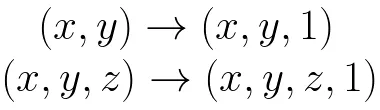

What are the advantages of using homogeneous coordinates?
Homogeneous coordinates are used can be greatly simplified point line three-dimensional space expression and rotational translation and other operations, the following points will be described with particular points.
Can 1 is conveniently expressed as the point on the line or plane
On a 2D plane, a straight line l can equation ax + by + c = 0 are represented, then the straight line is represented by a vector denoted generally
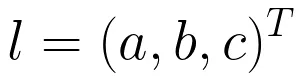
We know that the point p = (x, y) at the necessary and sufficient conditions on the line l is ax + by + c = 0
If you are using homogeneous coordinates, then, homogeneous coordinates of the point p is
p′=(x,y,1)
Then ax + by + c = 0 can use the inner product of two vectors (dot) to represent:

Therefore, necessary and sufficient conditions on a straight line point p l and p l is linear homogeneous coordinates p 'of the inner product:
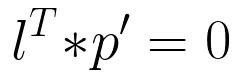
It is not very easy to do!
Similarly, we know that a plane A three-dimensional space can be expressed by Equation ax + by + cz + d = 0 to represent a three-dimensional space of the point P = (x, y, z) of the homogeneous coordinates P '= (x, y, z, 1), Similarly, the point P on the space plane a product of two vectors can be represented as follows:
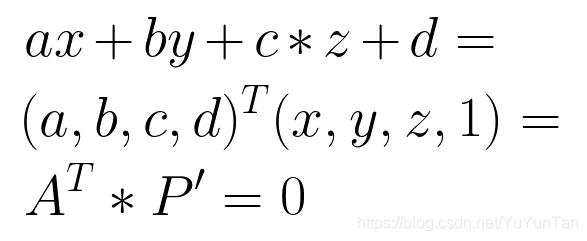
Accordingly, the point P on the necessary and sufficient condition is that the plane of plane A and P A vector of homogeneous coordinates of P 'of the inner product (dot product):
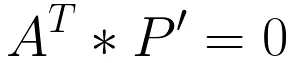
2 to facilitate expression of intersection of the line and the straight line, a plane and a plane
先给出结论,后面再具体解释:
结论:在齐次坐标下,可以用两个点 p, q 的齐次坐标叉乘结果来表达一条直线 l,也就是
l=p×q
也可以使用两条直线 l, m 的叉乘表示他们的交点 x
x=l×m
见下面示例图。
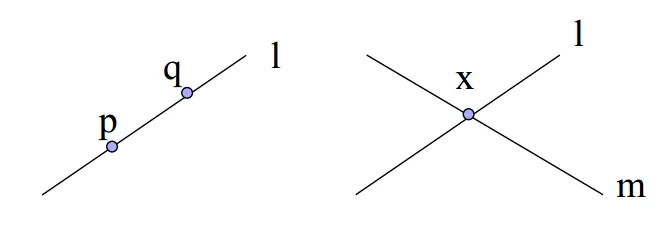
之所以可以这么简洁的表示交点是因为采用了齐次坐标的表示方式。
那么这是为什么呢?
先介绍一下叉乘(也称叉积、外积)的概念:
两个向量 a和b 的叉乘仅在三维空间中有定义,写作 a x b
a x b 是与向量 a, b都垂直的向量,其方向通过右手定则(见下图)决定。
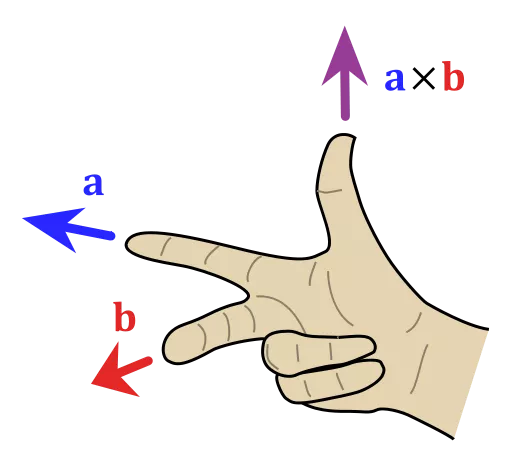
其模长等于以两个向量为边的平行四边形的面积(见下图)。
叉乘可以定义为:

其中 θ表示a, b的夹角(0°到180°之间),||a||, ||b||是向量a, b的模长
n则是一个与向量a, b所构成的平面垂直的单位向量
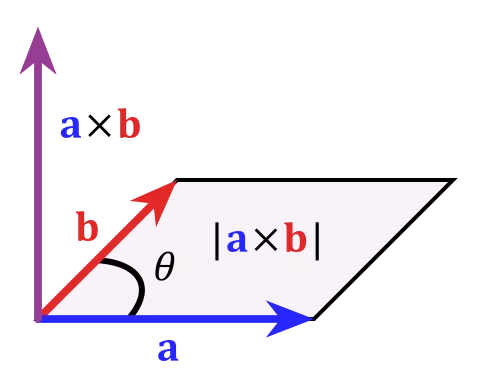
根据叉乘定义:
向量自身叉乘结果为0,因为夹角为0。也就是说三维向量 a x a =0, b x b = 0而点乘(也称点积,内积)的定义是
a∗b=∣∣a∣∣∗∣∣b∣∣∗cos(θ)
根据定义:如果两个向量垂直,cos(θ) = 0,点积也为0。
好了,经过上面点乘和叉乘定义的铺垫。下面来推导一下上面的结论:
为什么两条直线 l, m 的叉乘 l x m 等于它们的交点 p,也就是 p = l x m?
原因如下:首先,根据前面叉乘的定义,l x m 的结果向量(记为 p = l x m) 与 l 和 m都垂直,根据点乘的定义,垂直的向量之间的点积为0,因此可以得到:
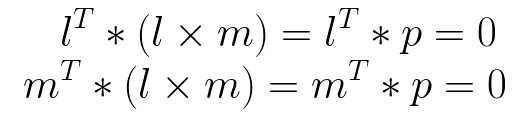
因此,根据前面点在直线上的结论,可以看到p既在直线l 上又在直线m上,所以 p = l x m 是两条直线的交点。此处 p 是齐次坐标。
同样的,可以证明,两点p, q 的叉乘 可以表示 过两点的直线l,即 l = p x q。(留做作业)
先给出结论:
(1)从普通坐标转换成齐次坐标时
如果(x,y,z)是个点,则变为(x,y,z,1);
如果(x,y,z)是个向量,则变为(x,y,z,0)
(2)从齐次坐标转换成普通坐标时
如果是(x,y,z,1),则知道它是个点,变成(x,y,z);
如果是(x,y,z,0),则知道它是个向量,仍然变成(x,y,z)
具体解释见:
http://www.cnblogs.com/csyisong/archive/2008/12/09/1351372.html
比如 两条平行的直线 ax+by+c=0, ax+by+d=0,
可以分别用向量 l = (a, b, c), m = (a, b,d)表示
根据前面直线交点的计算方法,其交点为 l x m
根据叉乘计算法则
向量

的叉乘结果可以用如下方法计算得到
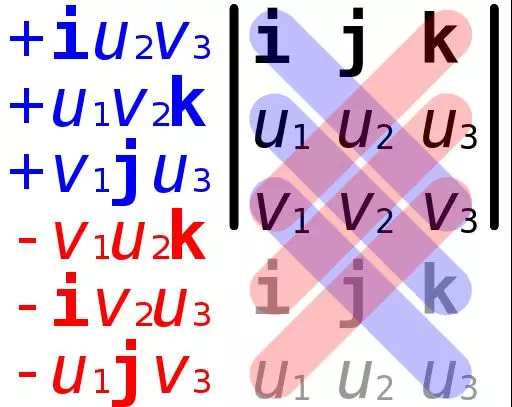
最终:l x m = (d-c)(b,-a,0),忽略标量(d-c),我们得到交点为(b,-a,0),并且是齐次坐标,如果要转化为非齐次坐标,那么会得到 (b/0, a/0),坐标是无穷大,可以认为该点为无穷远点,这与我们通常理解的:平行线相交于无穷远的概念相吻合。
因此,如果一个点的齐次坐标中,最后一个元素为0,则表示为无穷远点。
这是齐次坐标最重要的一个优势之一。在以后的学习中你会更加深刻的理解。
Using homogeneous coordinates, it can easily be converted to the multiplication addition, facilitate translation of the expression.
To complete the example, we will 2D coordinate point x = [u, v] 'translational t = [tu, tv], if non-homogeneous method, then, with the following addition
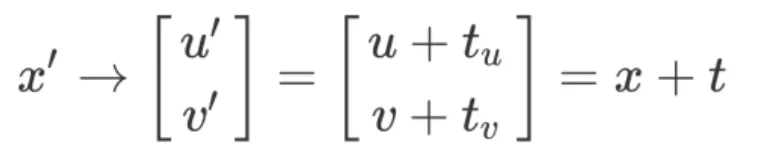
It can be converted to an addition if multiplication is represented by a homogeneous coordinate
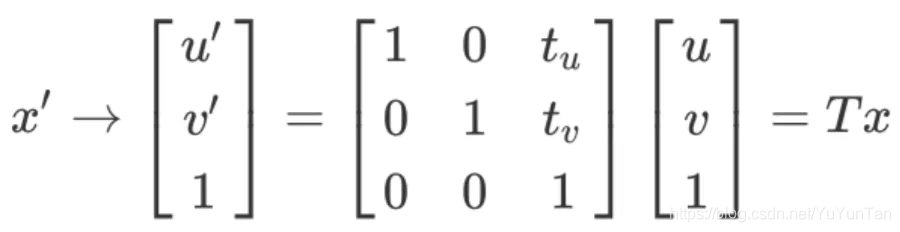
Euclidean transformation are generally two operations: translation and rotation.
If we want to be a standard vector a Euclidean transformation, usually by rotating the first rotation matrix R, then use the translational vector t, the result a '= R * a + t, this seems no problem.
However, we know that generally are contiguous SLAM Euclidean conversion, so there will be many successive rotation and translation, assume we conducted two vectors a Euclidean transformation, respectively, R1, t1 and R2, t2, respectively, get:
b=R1∗a+t1,c=R2∗b+t2
The end result $ C = R2 * (Rl + A * T1) + T2 $
Obviously, such a transformation after repeated will become more and more complex . The fundamental reason is the above expression is not a linear transformation relations .
At this time, on the show homogeneous coordinates of its charm, if expressed using homogeneous coordinates a '= R * a + t words can be written as:

A rotation and translation matrix T can be represented by the transformation matrix T is called matrix (transform matrix), so that a Euclidean transformation becomes linear, multiple Euclidean transformation by the transformation matrix even only on the line, such as in front of two Euclidean transform using homogeneous coordinates can be expressed as:

Which represents the tilde homogeneous coordinates. Generally, in the SLAM, b = Ta default form are homogeneous coordinates.
About the advantages of homogeneous coordinates there, what does? Leave a comment to add.
operation
Proof: Two p, q can be expressed by the cross points of the line l, i.e. l = pxq
(Hint: refer to earlier in this article demonstrate)