A scalar is a single number! There is also a more profound term for scalar, which is a quantity that does not change during linear transformation. There are many kinds of numbers:

Natural number
integer (positive or negative)
Rational numbers (including integers, infinitely recurring decimals or = integers/integers)
Real numbers (including rational and irrational numbers)
complex numbers (including real and imaginary numbers)

1.2 vector vector / vector

A vector vector is also called a vector, which represents an ordered array of n numbers
A vector can also be considered as an array list, such as [1,2,3,4,5]
In a two-dimensional graph in various vector spaces, in a three-dimensional graph, it is a point in the space (the end point represents a vector starting from the origin)
Vector, which can be considered as a direction, the direction is the sorting of the numbers in the array

Vectors can correspond to array lists in many languages, such as [1,2,3,4,5]
The vertical ones are called column vectors, α={x1,x2,x3....xn}
The horizontal one is a row vector, αT={x1,x2,x3....xn}

1.2.1 What is a vector

A vector is a set of numbers, not a single number, α={x1,x2,x3....xn}

1.2.2 How to represent a vector? Representation in vector space

In a general vector space, a vector is a ray segment starting from the origin
The starting point of the line segment must be the origin, and the end point of the line segment is the content of the vector (x1,x2) or (x1,x2,x3) or others, which are also the coordinates of the vector in this vector space

So this vector space is characterized by

A vector space must have an origin
Each vector is a ray line segment starting from the origin , and the vector can be represented by the coordinates of the end point
There is no parallel relationship between two vectors, at most two vectors are on the same straight line

1.3 Matrix

A matrix is a two-dimensional array, each element of which is determined by two indices A(i,j)
In many programming languages, each row is regarded as an object, and each column is regarded as an attribute/feature
It can be said that a matrix is a 2-dimensional array
Matrix A(i,j) such as ( a11,a12 ; a21,a22 )

1.3.1 Relationship between matrices and vectors

Viewpoint 1

basic point of view
A matrix is composed of multiple vectors, generally considered to be composed of multiple column vectors (bases)
A matrix is a coordinate in N-dimensional space that contains multiple vectors

Viewpoint 2

When computing, it can be considered that a vector is a special kind of matrix
A column vector is a column matrix
A row vector is a row matrix

1.3.2 Square matrix

In the matrix, the matrix with the number of rows = the number of columns is called a square matrix
Phalanx has many nice special properties

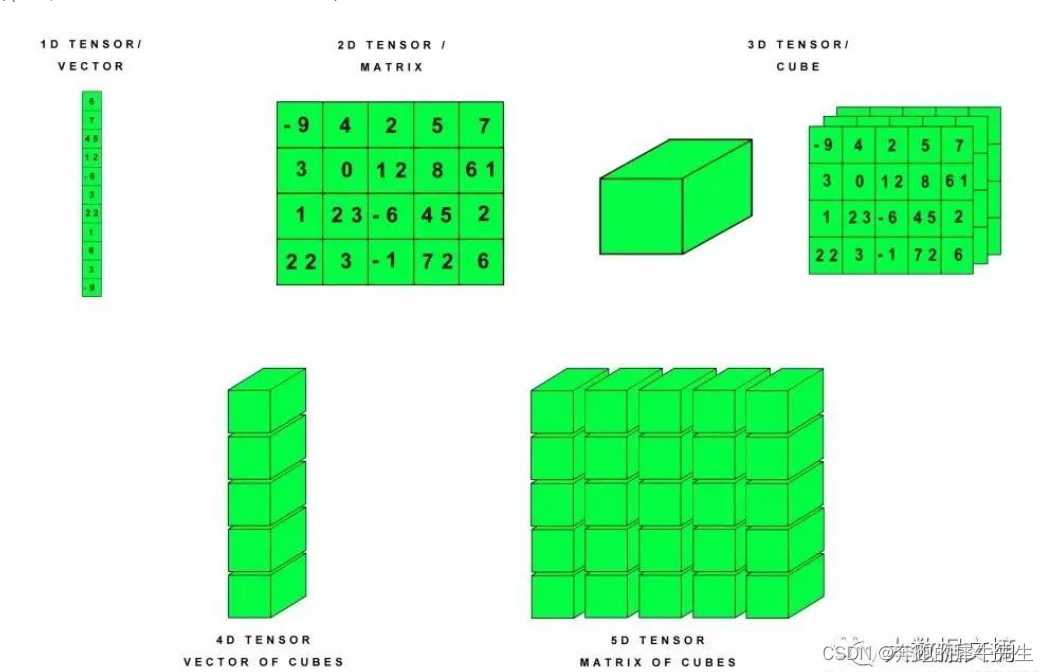
1.4 Tensor: scalars, vectors, and matrices can all be regarded as tensors

It can be said that a tensor is a 2-dimensional array
Matrix A(i,j,k) such as ( a11,a12 ; a21,a22 ; a31,a32 )
Tensor definition

A scalar of numbers, called a rank 0 tensor
An array of such vectors, (1,2), is called a rank 1 tensor (equivalent to 1 dimension)
Such a matrix of 2 arrays, such as (1,2;1,1), is called a tensor of order 2 (equivalent to 2 dimensions)
An array of more than two dimensions, such as a three-dimensional A(i,j,k), is called a third-order tensor

1.5 Examples

Pay attention to the wording:

Quantity → comma Quantity of a dimension
dimension → semicolon; separates different dimensions

Scalar: 1, 5, 11, 101, 999, etc.
vector

1D vector (0,1,2) or (1,2,3... 1001)
2-dimensional vector (0,1,2; 3,4,5) or [[0,1,2]; [3,4,5]] or [[1,2,3...... 1001] , [1,2] ]

tensor

3-dimensional vector -- scalar [[1,0,0][0,1,0][0,0,1]]

The following are 2 pictures from the Internet, not mine

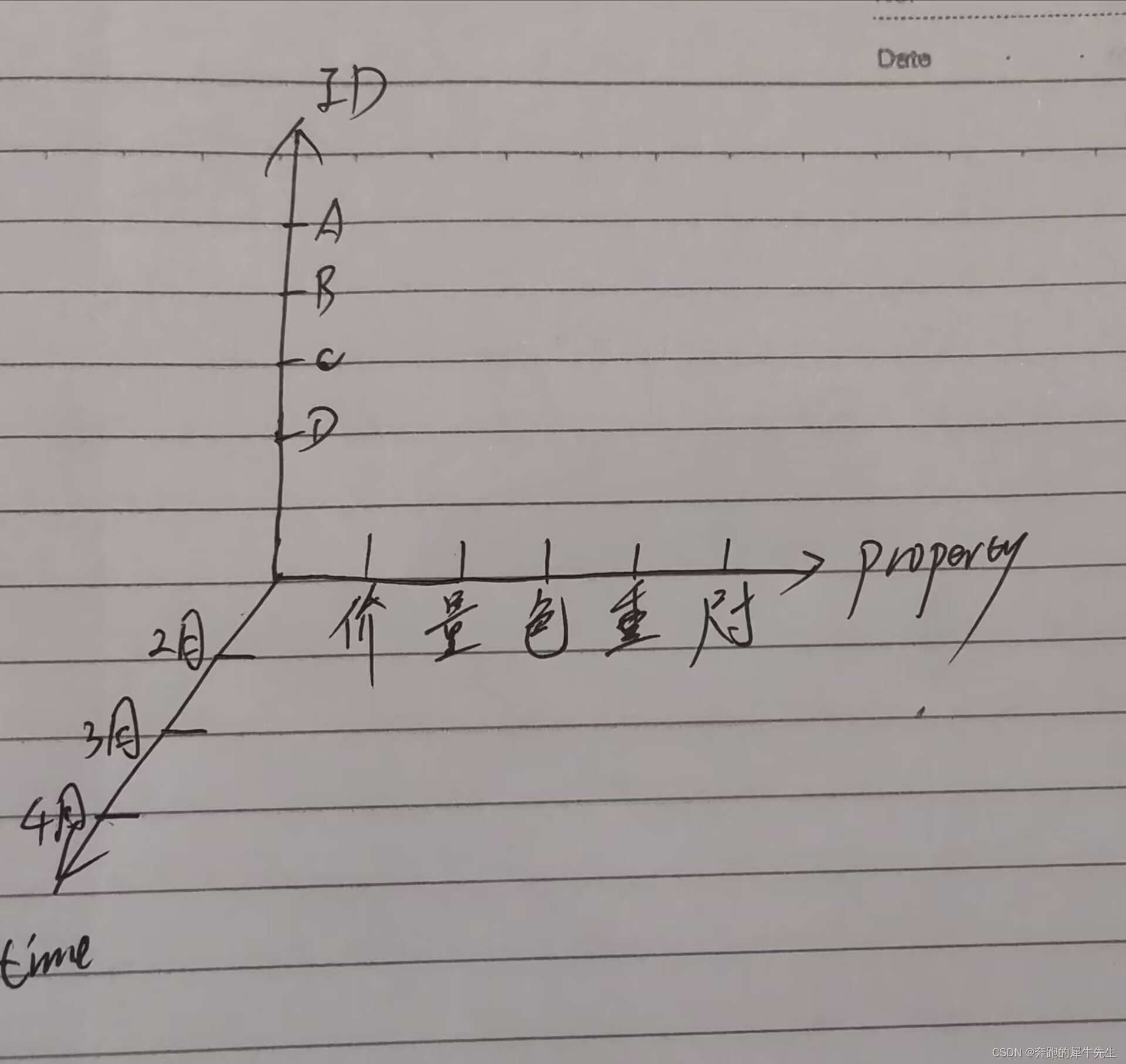
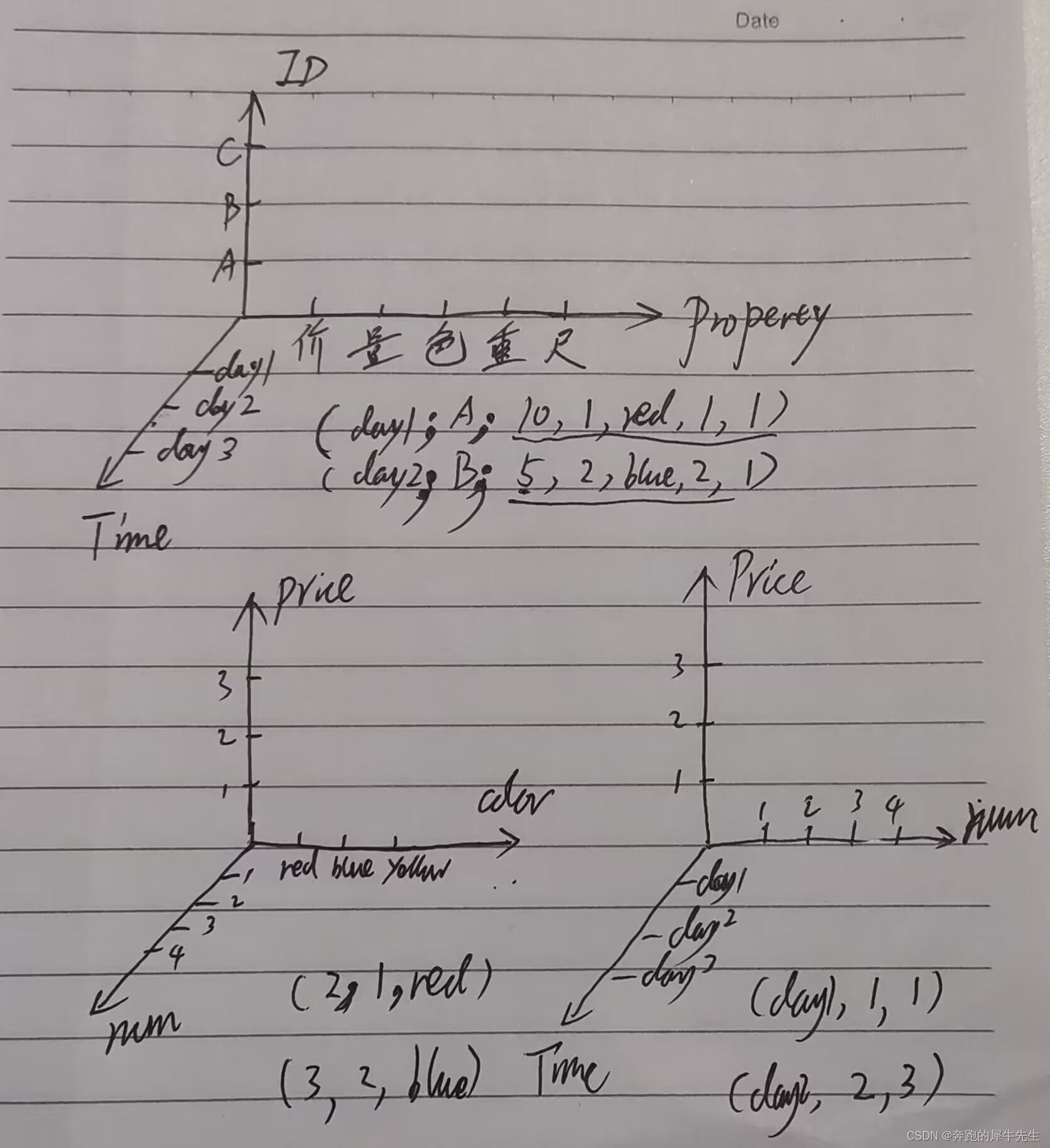
1.6 The following examples (generally still controversial? -- you can choose the handling method flexibly)

The following table is still a 2-dimensional table in appearance, but it can also be regarded as an N-dimensional tensor?
It can be flexibly designed to be 2-dimensional or 3-dimensional, because you can choose to combine some attributes into the same dimension

	price	quantity	color	weight	size
A	10	5	red	10	5
B	50	2	blue	3	2
C	100	1	yellow	1	1
D	30	10	green	5	3

And this is a tensor?
3 axes
If you think of time as the Z axis.
Then x is ID and y is property, which means that ID-price, ID-quantity, ID-color,,,, can form N two-dimensional tables, and these two-dimensional tables can be stacked together. Formed the Z axis?
It can be flexibly designed to be 2-dimensional or 3-dimensional, because you can choose to combine some attributes into the same dimension
The price, quantity, color, weight, size, etc. of dimension 1 can be regarded as a dimension and made into a three-dimensional coordinate axis. It can also be expanded into multiple dimensions, depending on the specific needs of data processing

1.7 Tensors with more dimensions, for example

3D = time series
4 dimensions = image
5 dimensions = video

2 What is a vector space, the spanning space of vectors?

When it comes to space, we need to start with more complex concepts

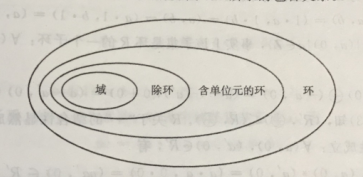
2.1 Repost: insert an analysis of other concepts in mathematics: group, ring, field, set, definition of space (meaning I don’t understand, just mark it)

This section is an excerpt
Set: A set can be understood as an unordered collection of objects
Group: A group is a set with specific operations and properties. The group introduces a binary operation (such as addition or multiplication) on the basis of the set, and satisfies the four elements of closure, associative law, identity element, and inverse element. The property can be understood as the sum of any two elements is still in the group, which is called a group. The group has only one addition operation?
Ring: The earliest refers to the integer ring, and later the ring is also called algebra, which has become the standard object of algebra. The ring is another operation added on the basis of the group, and it satisfies certain properties. Thus, a ring is an extension and enhancement of the concept of a group. A ring is an algebraic structure that involves two operations, usually addition and multiplication. The ring needs to satisfy addition to form a group, and multiplication to satisfy closure, associative law, and distributive law.
Domain: Domain is a very abstract concept. Domain implies a sufficiently large concept. In algebra, it can perform addition, subtraction, multiplication, and division operations. In mathematical logic, a defined set of functions is called a domain. The range is called the value range, and the set of all mathematical objects is called the domain of discourse in model theory. Domains used to be called entities. On the basis of the ring, the field requires multiplication (except for elements other than the multiplicative identity element) to also form a commutative group, that is, the multiplication needs to satisfy the commutative law, the properties of the identity element and the inverse element. In short, domains are rings that satisfy stricter properties. Therefore, a domain is an extension and enhancement of the concept of a ring.
Space: Visible space is also related to these esoteric concepts

What are the strict mathematical definitions of groups, fields, and rings in mathematics? - Zhihu defines a binary operation on a set and calls it addition. Now here are these rules: 1) Associative law: for any 2) existence... https://www.zhihu.com/question/449089514/answer/1777658855 Mathematics [1] about groups, rings, domains, modules-Know It may be a little messy to read, and there may be some grammatical oddities, don't worry about it...Introduction-Natural number collection Let's talk about natural numbers first, without citing its precise definition, let's quickly explain: "All numbers greater than 0 Integers are called natural numbers. (Here 0 is not considered a natural number)" Then all... https://zhuanlan.zhihu.com/p/336562401?utm_id=0

insert image description here

2.2 Scalar spaces

only single numeric scalars
contains multiple scalars
Scalar addition, subtraction, multiplication and division, etc. are also shown as closed
Any two scalars in the set of scalars can be added and multiplied to get another scalar. If these two operations satisfy the requirements of closure, associativity, commutation, and inverse elements, then these scalars form a scalar field. The scalars we are familiar with include real numbers, complex numbers, and rational functions.

2.3 Vector space (vector space or linear space linear space)

First, there are two kinds of objects in linear space, scalar and vector.
is the most important mathematical space. Vector spaces contain two different kinds of entities—vectors and scalars. In addition to operations between two scalars, scalar-vector multiplication and vector-vector addition are also defined in vector spaces.
Vector space, as can be seen from the drawing, whether it is a 2-dimensional or 3-dimensional vector space, it is a ray line segment divided from the origin, and the end point coordinates can represent this vector''

2.3.1 Linear space definition

Linear space refers to that there is a set composed of "fixed-length coordinate sequences" called "vectors", and then between the vectors in this set, two operations "addition" and "number multiplication" are defined , the combination of the two (the algebraic structure formed) is called a linear space. Of course, there is an additional requirement, that is, closure : any vector in this set can legally perform these two operations, and the result is still in this set.

If it is not closed, mathematicians feel that it is better to include the newly calculated thing into the existing research objects. After all, they also want to study "all the same kind". So this closure is required.

a collection of vectors
This set, and the algebraic operations defined on it, is the linear space
This linear space is compared to the operation space of general integers and functions of ordinary single number operations

2.4 Affine space

The difference between affine space and linear space is that it adds another object, which is a "point".
Contains: points, scalars, and vectors
And they are also different in operation rules.
Affine space is an extension of vector space. In addition to scalars and vectors, it also contains another object---point. Although there is no operation defined for two points and a scalar in affine space, an operation is defined for a vector and a point—vector-point addition, whose result is a point. It can also be said that there is an operation called point-to-point subtraction, which obtains a vector from two points.

Or it can be understood in this way: affine space assumes that we have defined the vector space, and then define a set of points, and at the same time stipulate the sum operation between the point and the vector (the result of the sum is still the search point), this point The set is the affine space that accompanies this vector space.

The difference between affine space and linear space

The linear space must satisfy the closure of addition and multiplication operations , that is, for any vector u, v and scalar a, b, u+v and au+bv must belong to the linear space.
The affine space only needs to satisfy that vectors can be subtracted, and vectors can be added and subtracted, and it is not necessary to satisfy the closure of multiplication operations.
There exists a zero vector in linear space, i.e. adding it does not change the value of the vector.
There is no notion of a zero vector in an affine space.
Vectors in linear space have the concept of magnitude and direction, and can be compared quantitatively.
A vector in an affine space has only the concept of direction, not the concept of magnitude.
A vector in a linear space can be represented by a coordinate system, and the coordinates of the vector are unique, that is, the end point.
A vector in an affine space cannot be represented by a coordinate system, but can only be represented by the relationship between vectors.
A vector space in a linear space is a linear subspace, that is, its subset also satisfies the conditions of a linear space.
An affine space in an affine space is not an affine subspace, nor does its subset necessarily satisfy the conditions of an affine space.

2.5 Euclidean space

Affine space is equivalent to Euclidean space, which removes the concept of distance (retaining length ratio) and angle, and only retains the length ratio on straight lines, straight lines parallel and parallel straight lines
Euclidean space refers to the coordinate space (each component of the coordinate is defined on the domain), which specifies the addition and multiplication of coordinates (here, called vector space), (note that the following is the key!) and defines Inner product between coordinates. After the inner product is defined, the distance between different coordinates in space and the angle between their directions can be specified, and the geometric structure required by Euclidean geometry is obtained.

3 Vector space: it is the spanning space of vectors

3.1 Definition of vector space

In short: a vector space is the spanning space of vectors
is the spanning space formed by the results of all linear combinations of the specified vectors

First there is the concept of "linear combination"

All linear combinations of a set of linearly independent vectors (basis) form new vectors (coordinates), and the space they all form is called the vector spanning space.
For example, a vector group {v1,v2...vn} can be 2, 3 or more
But generally it is 2 vector groups - form the XOY plane, and 3 vector groups form the XOYOZ space
V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
That is to say, if a certain vector group {v1,v2...vn} performs any linear combination (addition and scalar multiplication), the result is still in the vector space, which is the closure, so.

Closure of addition and multiplication

The concept of linear combination first -- represents the closure of a calculation result, and is still within this space
The linear space satisfies two "operational closures". For the defined "addition" and "number multiplication", assuming that α and β are randomly selected from the space, then:

γ=α+β is also in the space (in the set)
η=kα is also in the space (in the set)

3.2 Linear correlation, specifically mentioned

Note here that α1 is an array/vector, not a specific number in the array, such as α1={x1,x2...}

(Linear algebra matrices, etc. are definitely studying the relationship between arrays/vectors, not the relationship between individual numbers)

If there are multiple vectors in A: α1, α2, α3, ..... αn, if there is a set of real numbers k1, k2, k3....kn that are not all 0, k1*α1+ k2*α2+ ...+ kn*αn=0 ,

Then these vectors α1, α2, α3, α4, ..... αn are linearly related

3.3 Meaning of linear combination

For example, a vector group {v1,v2...vn} can be 2, 3 or more
But generally it is 2 vector groups - form the XOY plane, and 3 vector groups form the XOYOZ space
V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
That is to say, any linear combination of a certain vector group {v1,v2...vn}, the result is still in the vector space.

3.3.1 Specific method of linear combination

Methods for linear combinations include the following:

addition
scalar multiplication

3.4 Linear Transformation

Linear transformation includes linear transformation of rows and linear transformation of columns

Linear Transformation of Rows

between lines, exchange
multiply a row by a multiple
Multiply a row by a multiple + to other rows

Linear Transformation of Columns

Between columns, exchange
a column multiplied by a multiple
Multiply a column by a multiple + to other columns

3.5 What is the meaning of linear transformation (linear mapping)?

Linear transformation refers to the linear space, satisfying

T(a+b)=T(a)+T(b)

T(kα)=kT(α)

So what does this have to do with straight lines?

See the definition of linear correlation, this has a great relationship with positive and negative proportionality, and there is also a relationship with a straight line!
Scalar multiplication: number multiplication operation, which can be regarded as stretching + direction transformation on a straight line
Addition operation: It can be explained by the triangle rule and the form of first-digit connection. Two segmented vectors can be equivalent to one total vector. The graph generated is still a straight line.
This kind of mapping maps the original straight line in the space into a straight line without "distorting" it into a curve;
At the same time keep the origin still (the origin moving is called "affine transformation"...)

Learning and organizing linear algebra 3: What are scalar vectors and tensors? What is a vector space?

1 Scalars and vectors

1.1 Scalar scalar