content
1. The concept and structure of the tree
2. The concept and structure of binary tree
storage structure of binary tree
1. The concept and structure of the tree
tree concept
- Real tree:
- Tree in data structure:
A tree is a nonlinear data structure, which consists of n (n>=0) finite nodes to form a set with hierarchical relationship. It is called a tree because it looks like an upside-down tree, which means it has the roots up and the leaves down.
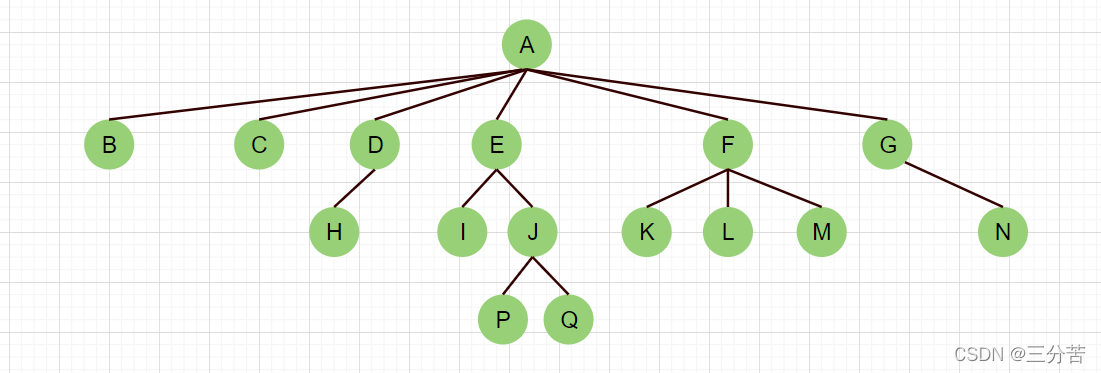
- As shown in the figure:
Features:
- There is a special node, called the root node, the root node has no predecessor nodes
- Except for the root node, the remaining nodes are divided into M(M>0) sets T1, T2, ..., Tm that do not intersect with each other, and each set Ti(1<= i<= m) is a structure with tree-like subtrees. The root node of each subtree has one and only one predecessor, and can have 0 or more successors
- Therefore, the tree is defined recursively.
Notice:
- In a tree structure, there can be no intersection between subtrees, otherwise it will not be a tree structure.
- Except for the root node, each node has one and only one parent node.
- A tree of N nodes has N-1 edges.
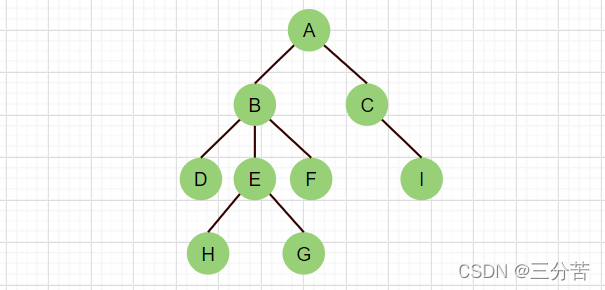
- As shown in the figure: (The following two are not trees)
proper noun for tree
- Proper noun:
- Degree of a node: The number of subtrees contained in a node is called the degree of the node; as shown above: A is 6
- Leaf node or terminal node: a node with a degree of 0 is called a leaf node; as shown in the figure above: B, C, H, I... and other nodes are leaf nodes
- Non-terminal nodes or branch nodes: nodes whose degree is not 0; as shown in the figure above: D, E, F, G... and other nodes are branch nodes
- Parent node or parent node: If a node contains a child node, the node is called the parent node of its child node; as shown above: A is the parent node of B
- Child node or child node: The root node of the subtree contained in a node is called the child node of the node; as shown above: B is the child node of A
- Sibling nodes: nodes with the same parent node are called sibling nodes; as shown above: B and C are sibling nodes
- The degree of the tree: in a tree, the degree of the largest node is called the degree of the tree; as shown above: the degree of the tree is 6
- The level of nodes: starting from the definition of the root, the root is the first layer, the child nodes of the root are the second layer, and so on;
- The height or depth of the tree: the maximum level of nodes in the tree; as above: the height of the tree is 4
- Cousin node: nodes whose parents are in the same layer are cousins of each other; as shown above: H and I are sibling nodes of each other
- Ancestors of a node: all nodes on the branch from the root to the node; as shown above: A is the ancestor of all nodes
- Descendants: Any node in the subtree rooted at a node is called the descendant of the node. As shown above: all nodes are descendants of A
- Forest: A collection of m (m>0) disjoint trees is called a forest;
- The nearest common ancestor: The nearest ancestor to some nodes, for example, the nearest common ancestor of P and Q is J, and the nearest common ancestor of K and F is F. The node itself can also become its own ancestor
- expand:
After knowing the above proper nouns, you can try to calculate the relationship between the total number of nodes and the number of edges :
Assuming that the total number of nodes is n, then the number of edges is n-1, how to calculate it? Obviously, the edge is the bracket connecting each node, as shown in the black line above. Assume that the degree of the tree is x, and it is known from the proper noun that the degree of the tree is the number of degrees of the largest node, and the number of nodes with degree i is ni, then the total number of nodes is the sum of these nodes , ie n=n0+n1+n2+n3+...+n(i-1)+n(i)
In summary:
- Number of sides: n-1
- Total number of nodes: n=n0+n1+n2+n3+...+n(i-1)+n(i)
Example introduction:
- Answer: C
- Parse:
Let the number of nodes with degree i be ni, and the tree has a total of n nodes, then n=n0+n1+n2+n3. The total number of edges in a tree with n nodes is n-1. According to the definition of degree, the relationship between the total number of edges and the degree is n-1=0*n0+1*n1+2*n2+3*n3. According to the meaning of the question: n3=2, n2=1, n1=2. Solve the two equations simultaneously, you can get n0 = n2 + 2n3 + 1, n0=6, choose C.
representation of tree
The tree structure is more complicated than the linear table, because the number of children is not known. But if the degree of the tree is known, it is well defined.
//假设指定树的度,可以直接定义 #define N 5 struct TreeNode { int data; struct TreeNode* subs[N]; //指针数组,每个结点存5个 };But there is another flaw. Since the degree of the tree is 5, but you can only set the degree of each node to be 5, but in fact, you only need to ensure that the degree of each node is <= 5, so It can be seen that this method leads to a waste of space. In addition, if the degree of the tree is not known, it is difficult to define the above method. The following scheme can be used:
- Child brother notation:
Since the value range is preserved, the relationship between nodes and nodes must also be preserved. In practice, there are many representations of trees, such as parent representation, child representation, child parent representation, and child sibling representation. Here we simply understand the most commonly used child brother notation.
//孩子兄弟表示法 typedef int DataType; struct TreeNode { struct TreeNode* firstChild1; // 第一个孩子结点 struct TreeNode* pNextBrother; // 指向其下一个兄弟结点 DataType data; // 结点中的数据域 };
- Draw a picture to demonstrate the process:
Suppose we want to represent the following tree:
The physical structure is as follows:
It can also be understood like this:
Explain the principle:
From the above code picture demonstration and the appearance of the tree, we know that the root node A has two children, B and C. Always let A's leftchild point to the first child B, and A's other children C let B's brother pointer go to Pointing to, C has no brothers, and points directly to NULL. In the same way, B has 3 children, let the leftchild pointer point to the first child D, then let D's brother pointer point to the next E, and so on... This method shows how many children a node has. It doesn't matter, let the father point directly to the first child, and the remaining children are linked with the child's sibling pointer.
The use of trees in practice
- (represents the directory tree structure of the file system)
2. The concept and structure of binary tree
concept
Binary tree: a tree of degree 2 , a binary tree is a finite set of nodes , the set:
- or empty
- Consists of a root node plus two binary trees called left and right subtrees
As shown in the figure:
As can be seen from the above figure:
- There is no node with degree greater than 2 in a binary tree
- The subtree of a binary tree is divided into left and right, and the order cannot be reversed, so the binary tree is an ordered tree
Note: For any binary tree, it is composed of the following situations:
real binary tree
What was the first thing you said when you saw a tree like this?
Are you sighing, for example, how can there be such a symmetrical tree, or even a national quintessence, I think it's okay haha... After learning the " special binary tree " below, you will have a new understanding.
special binary tree
- Full binary tree: A binary tree, if the number of nodes in each layer reaches the maximum value, the binary tree is a full binary tree. That is, if a binary tree has K levels and the total number of nodes is 2^k -1 , then it is a full binary tree.
- Complete binary tree: A complete binary tree is a highly efficient data structure, and a complete binary tree is derived from a full binary tree. For a binary tree of depth K with n nodes, it is called a complete binary tree if and only if each node of the tree corresponds one-to-one with nodes numbered from 1 to n in the full binary tree of depth K. Note that a full binary tree is a special kind of complete binary tree.
In simple terms, each node of a full binary tree has degree 2, and a full binary tree is a special case of a complete binary tree. When the depth is K, the complete binary tree is a full binary tree in the interval of [1, k-1] layers, and only the Kth layer of the last layer is not full, but the last layer is continuous from left to right. Icon:
After learning this, when you see the real binary tree in the picture above, can you say, wc! Isn't this a pure full binary tree?
Properties of Binary Trees
Property 1: If the specified level of the root node is 1, then there are at most 2^(i-1) nodes on the i-th level of a non-empty binary tree.
Property 2: If the number of levels of the root node is specified to be 1, the maximum number of nodes of a binary tree with a depth of h is 2^h - 1 .
Property 3: For any non-empty binary tree, if the number of leaf nodes with degree 0 is n0, and the number of branch nodes with degree 2 is n2, then n0 = n2 +1
Property 4: If the level of the root node is specified as 1, the depth of a full binary tree with n nodes, h= log2(N+1) .
Property 5: For a complete binary tree with n nodes, if all nodes are numbered from 0 in the array order from top to bottom and from left to right, then for the node with sequence number i:
- 1. If i>0, the parent sequence number of the node at i position: (i-1)/2; i=0, i is the root node number, and there is no parent node
- 2. If 2i+1<n, the left child number: 2i+1, 2i+1>=n otherwise there is no left child
- 3. If 2i+2<n, the right child sequence number: 2i+2, 2i+2>=n otherwise there is no right child
Note: The relevant knowledge of property 5 will be expanded in the following storage structure.
Example presentation:
- Example 1:
- Answer: B
- Parse:
Using property 3 directly, the leaf node is the degree of 0, and n0 is always 1 more than the node with n2 degree of 2, so n0=200, choose B.
- Example 2:
- Answer: A
- Parse:
It is known from the previous article that the maximum degree of each node of a complete binary tree is 2, the minimum is 0, and the number of nodes with degree i is ni, where i belongs to [0, 2], and only a trilogy is required.
- The total number of nodes is 2n, then 2n=n2+n1+n0,
- Because it is a binary tree, there is n0-1=n2, then the formula becomes n0-1+n1+n0=2n.
- And because of the complete binary tree, n1 can only be 0 or 1, and it is necessary to ensure that the result is an integer, so n1 is 1. In summary, n0=n
- Example 3:
- Answer: B
- Parse:
This question is actually not complicated. Through the complete binary tree and the number of nodes, we can deduce the range of heights to lock the answer.
- Assuming that the height is h, when the number of nodes is the most, the binary tree is a full binary tree, then the property 2, 2^h-1=531 is satisfied, and h is log2(532), which is the lowest value of height.
- When the number of nodes is the least, that is to say, the first to h-1 layers are all nodes of degree 2, and only the last layer, the h-th layer, has only one node. At this time, the formula: 2^(h-1)-1+1=531, the solution h is log2(531)+1, and this case is the highest value of the height of the tree
- As a result, the value range of the tree (log2(532), log2(531)+1) is rounded to obtain h as 10, choose B
storage structure of binary tree
Binary trees can generally be stored in two structures, a sequential structure and a chain structure.
- 1. Sequential storage
Sequential structure storage is to use arrays for storage. Generally, arrays are only suitable for representing complete binary trees, because not complete binary trees will waste space. In reality, only the heap will use the array to store it, and we will specifically explain the heap in the following chapters. Binary tree order storage is physically an array, and logically is a binary tree.
For example, we want to represent the following complete binary tree (logical structure)
At this point we try to use an array to store (physical structure)
We store the data of the tree in the above logical structure in the array, and use subscripts to represent different data for easy access. At this point, we have to imagine this array as a "tree", how to do it? as follows:
Just restore the array to look like a tree, as above.
- Now that the drawing is out, there is a problem. How to clarify the relationship between father and child?
First, assuming that the parent's subscript is parent , the left child's subscript is leftchild , and the right child's subscript is rightchild , the subscript relationship between parent and child is as follows:
- leftchild = parent*2 + 1
- rightchild = parent*2 + 2
- parent = (child - 1) / 2
Analysis: It is not difficult to find from the figure that the subscripts of all the left children are odd numbers, and the subscripts of the right children are even numbers, so it is not difficult to come up with the expressions of the left and right children. Instead, the expression of the father can be deduced.
- But in the father's formula, there is only (child - 1) / 2, and there is no distinction between left and right children. Why?
Here we assume that the subscripts of leftchild and rightchild are both 3. It is not difficult to find that the parent subscripts calculated are both 1. Similarly, when the left and right children are both subscripts of 4, the father's subscripts are calculated to be 1. This rule It can be known that the father can be directly represented by the child subscript, and there is no need to distinguish the left and right children.
- 2. Chain storage
The chain storage structure of a binary tree means that a binary tree is represented by a linked list, that is, a chain is used to indicate the logical relationship of elements. The usual method is that each node in the linked list consists of three fields, the data field and the left and right pointer fields. The left and right pointers are respectively used to give the storage addresses of the link nodes where the left and right children of the node are located. The chain structure is further divided into two-fork chain and three-fork chain. At present, we generally use two-fork chain in our study. Later, when we learn high-level data structures such as red-black tree, we will use three-fork chain.