Logistic regression formula derivation

1. The logistic regression model hypothesis is:, $h\theta (x)=g(\theta \top x)$ where X represents a feature vector, g represents a logistic function (logistic function) is a commonly used S-shaped logistic function, the formula is:, $\ g (z) = \ frac {1} {1 + e ^ {- z}}$ the image of the logistic function is:

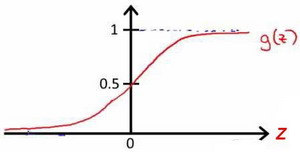
Since the value range of the g(z) function is 0-1, $h \theta (x)$ the understanding of this is: for a given input variable, the probability of the output variable=1 ( estimated probablity ) is calculated according to the selected parameters $h \theta(x)=P(y=1|x; \theta)$ . For example, if for a given x , h θ x =0.7 is calculated through the determined parameters , it means that there is a 70% probability that y is a positive category, and the corresponding probability that y is a negative category is 1-0.7= 0.3.

2. After the model function is determined, the loss function needs to be determined. The loss function is used to measure the difference between the output of the model and the real output.

Assuming that only two label 1 and 0, $in \ in \ left \ {0, \ right 1 \}$ . If we regard any set of samples collected as an event, then the probability of this event's occurrence is assumed to be p. The value of our model y is equal to the probability that the label is 1, which is p.

$p_{y=1}= \frac{1}{ 1 + e^{- \theta \top x}}=P$ $P_{y=1} = \frac{1}{1+e^{-\theta\top x}} = P$

Because the label is either 1 or 0, the probability of the label being 0 is: $P_{y=0} = 1-P$

We regard a single sample as an event, then the probability of this event occurring is:

$P_{(y|x))} = \left\{\begin{matrix} p, y=1& \\ 1-p, y=0& \end{matrix}\right.$

This function is not easy to calculate, it is equivalent to:

$P_{y_{i}|x_{i}} = p^{y_{i}} * (1-P)^{1-y_{i}}$

To explain the meaning of this function, we have collected a sample $\left ( x_{i}, \right y_{i} )$ , and for this sample, $y_{i}$ the probability that its label is $p^{y_{i}}(1-p)^{1 - y_{i}}$ . (When y=1, the result is p; when y=0, the result is 1-p).

If we collect a set of data, a total of N $\left \{ (x_{1}, y_{1}), (x_{2}, y_{2}), (x_{3}, y_{3})...(x_{N}, y_{N}) \right \}$ ,, how to find the total probability of this combined event? In fact, it is enough to multiply the probability of each sample occurrence, that is, the probability of collecting this set of samples:

$P_ {total} = P (y_ {1} | x_ {1}) P (y_ {2} | x_ {2}) P (y_ {3} | x_ {3}) ... P (y_ {N} | x_ {N})$

$= \prod_{n=1}^{N} p^{y_{n}} (1-p)^{1-y_{n}}$

Since continuous multiplication is very complicated, we take logarithms on both sides to turn continuous multiplication into continuous addition form, namely:

$ln (P_ {total}) = ln (\ prod_ {n = 1} ^ {N} p ^ {y_ {n}} (1-p) ^ {1-y_ {n}})$

$= \ sum_ {n = 1} ^ {N} ln (p ^ {y_ {n}} (1-p) ^ {1-y_ {n}})$

$= \ sum_ {n = 1} ^ {N} (y ^ {n} ln (p) + (1-y_ {n}) ln (1-p))$

among them $p=\frac{1}{1+e^{-\theta} \top x}$

This function is $J(\theta)$ also called its loss function . The loss function can be understood as a function that measures the difference between the output result of our current model and the actual output result. The value of the loss function here is equal to the total probability of occurrence of the event, and we hope that the larger the better. But it is a bit contrary to the meaning of loss, so you can also take a negative sign in front. and so: $J (\ theta) = - \ frac {1 {{n} \ sum_ {n = 1} ^ {N} (y ^ {n} ln (p) + (1-y_ {n}) ln (1-p ))$

3. According to the above, we know the gradient loss function of logistic regression $J(\theta)$ , then the gradient function can be obtained by finding the right $\theta$ partial derivative $J(\theta)$ .

$\bigtriangledown p(\theta)=\bigtriangledown (\frac{1}{1+e^{-\theta\top x}})$

$=- \frac{1}{(1+e^{-\theta\top x})^{2}} (1+e^{-\theta\top x})'$

$=- \frac{e^{-\theta\top x}}{(1+e^{-\theta\top x})^{2}} \cdot (-x)$

$=\frac{1}{1+e^{-\theta\top x}} \cdot \frac{e^{-\theta\top x}}{1+e^{-\theta\top x}} \cdot x$

$=p(1-p)x$

In the $J(\theta)$ derivation, $\bigtriangledown p(\theta)$ the following can be obtained:

$\bigtriangledown J(\theta) = \bigtriangledown -\frac{1}{m} (\sum_{n=1}^{N}( y_{n}ln(p) + (1-y_{n})ln(1-p)))$

$= \ sum_ {n = 1} ^ {N} (y_ {n} ln '(p) + (1-y_ {n}) ln' (1-p))$
$=-\frac{1}{n}\sum_{n=1}^{N} ((y_{n}\frac{1}{p}p') + (1+y_{n})\frac{1}{1-p}(1-p'))$

$= - \ frac {1} {n} \ sum_ {n = 1} ^ {N} (y_ {n} (1-p) x_ {n} - (1-y_ {n} px_ {n}))$

$=-\frac{1}{n}\sum_{n=1}^{N} (y_{n} - p)x_{n}$

$=-\frac{1}{n}\sum_{n=1}^{N}(y_{n} - \frac{1}{1+e^{-\theta \top x_{n}}})x_{n}$

$=\frac{1}{n}\sum_{n=1}^{n} ( \frac{1}{1+e^{-\theta\top x_{n})}} - y_{n})x_{n}$

4. According to the above, the definition of logistic regression can be obtained:
objective function: $h_{\theta}(x)=\frac{1}{1+e^{-\theta\top x}}$

Cost function: $J(\theta)=- \frac{1}{m} \sum_{n=1}^{N} (y^{n}ln(p) + (1-y_{n})ln(1-p))$

Gradient function: $\frac{\partial J(\theta)}{\partial \theta} = \frac{1}{n}\sum_{n=1}^{n}(\frac{1}{1+e^{-\theta\top x_{n}}} - y_{n})x_{n}$

Gradient descent process:

The gradient descent formula is:

$\theta_{j} := \theta_{j} - \alpha \frac{1}{m} \sum_{n=1}^{N}(h_{\theta}(x^{(n)}) - y^{(n)})x_{j}^{(n)}$ Among them $\alpha$ is the learning rate, you can choose: 0.01, 0.03, 0.1, 0.3, 1, 3, 10

Reference from: https://zhuanlan.zhihu.com/p/44591359

Logistic regression formula derivation

Guess you like