Autor: Yu Fan
Hintergrund
Die Entwicklung der künstlichen Intelligenz (KI) hat ein neues Paradigma für wissenschaftliche Entdeckungen eingeführt. Heute hat KI begonnen, unser Verständnis von Naturphänomenen auf einem breiten Spektrum räumlicher und zeitlicher Skalen zu verbessern, zu beschleunigen und zu ermöglichen, wodurch die Entwicklung der Naturwissenschaften vorangetrieben und das neue Forschungsfeld AI4Science ins Leben gerufen wurde. Ein kürzlich von mehr als 60 Autoren gemeinsam verfasster Übersichtsartikel „Künstliche Intelligenz für die Wissenschaft in Quanten-, Atom- und Kontinuumssystemen“ bietet eine ausführliche technische Zusammenfassung in den Teilbereichen subatomare, atomare und Kontinuumssysteme. Hier extrahieren wir das technische Rückgrat dieses Aufsatzes und konzentrieren uns auf die Konstruktion eines äquivarianten Modells unter Symmetrietransformation.
1. Einleitung
Im Jahr 1929 bemerkte der Quantenphysiker Paul Dirac: „Die grundlegenden physikalischen Gesetze, die für die mathematische Theorie des größten Teils der Physik und der gesamten Chemie erforderlich sind, sind uns bereits vollständig bekannt, und die Schwierigkeit liegt in der Tatsache, dass die genaue Anwendung dieser Gesetze dazu führt.“ komplex Dies gilt von der Schrödinger-Gleichung in der Quantenphysik bis zur Navier-Stokes-Gleichung in der Strömungsmechanik. Deep Learning kann die Lösung dieser Gleichungen beschleunigen. Mithilfe der Ergebnisse herkömmlicher Simulationsmethoden als Trainingsdaten können diese Modelle nach dem Training wesentlich schneller Vorhersagen treffen als herkömmliche Simulationen.
In anderen Bereichen wie der Biologie sind die zugrunde liegenden biophysikalischen Prozesse möglicherweise nicht vollständig verstanden und können letztendlich nicht durch mathematische Gleichungen beschrieben werden. In diesen Fällen können Deep-Learning-Modelle mithilfe experimentell generierter Daten trainiert werden, z. B. der Proteinvorhersagemodelle AlphaFold, RoseTTAFold, ESMFold und anderer durch Experimente gewonnener 3D-Strukturen, sodass die Genauigkeit rechnerisch vorhergesagter Protein-3D-Strukturen mit experimentellen Ergebnissen vergleichbar sein kann . .
1.1 Wissenschaftliche Bereiche
Die wissenschaftlichen Interessengebiete in diesem Artikel sind in der folgenden Abbildung im Überblick nach den räumlichen und zeitlichen Maßstäben des modellierten physikalischen Systems geordnet.
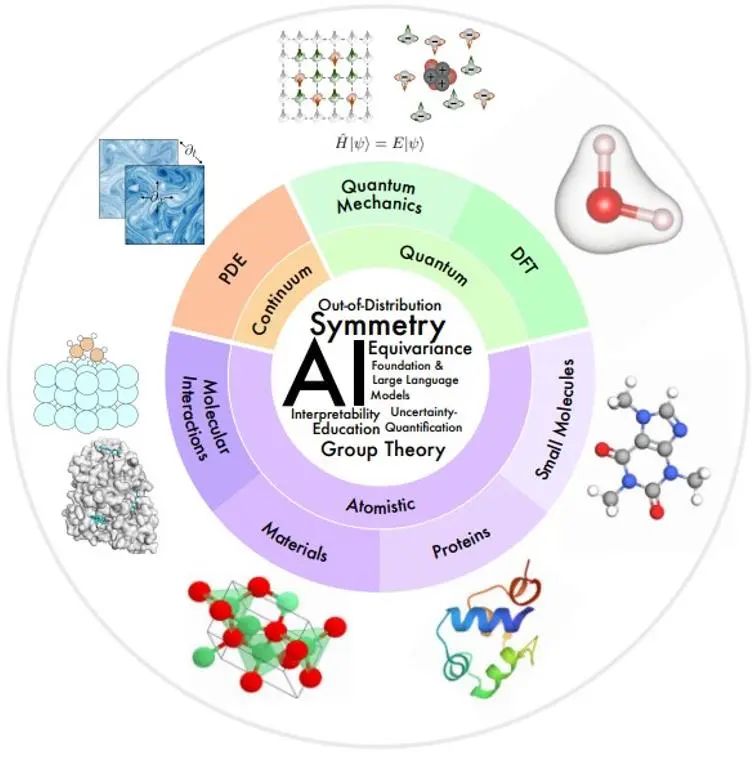
Kleiner Maßstab: Die Quantenmechanik nutzt die Wellenfunktion, um physikalische Phänomene im kleinsten Maßstab zu untersuchen. Die Schrödinger-Gleichung, der sie folgt, beschreibt den vollständigen dynamischen Prozess des Quantensystems, bringt jedoch eine exponentielle Komplexität mit sich. Die Methoden der Dichtefunktionaltheorie (DFT) und der Ab-initio-Quantenchemie sind in der Praxis weit verbreitete Methoden zur Berechnung der elektronischen Struktur und der physikalischen Eigenschaften von Molekülen und Materialien und können weiter auf die elektronischen und mechanischen Eigenschaften von Molekülen und Festkörpern schließen , magnetische und katalytische Eigenschaften. Allerdings sind diese Methoden immer noch rechenintensiv, sodass ihre Verwendung auf kleine Systeme (~1000 Atome) beschränkt ist. Das KI-Modell kann dabei helfen, Geschwindigkeit und Genauigkeit zu verbessern.
Mesoskala: Kleine Moleküle, typischerweise mit einer Größe von mehreren zehn bis hundert Atomen, spielen in vielen chemischen und biologischen Prozessen eine wichtige regulatorische und signalisierende Rolle. Proteine sind große Moleküle, die aus einer oder mehreren Aminosäureketten bestehen. Die Aminosäuresequenz bestimmt die Proteinstruktur, die wiederum ihre Funktion bestimmt. Die materialwissenschaftliche Forschung untersucht den Zusammenhang zwischen Verarbeitung, Struktur, Eigenschaften und Materialien. Molekulare Wechselwirkungen untersuchen, wie viele physikalische und biologische Funktionen durch molekulare Wechselwirkungen ausgeführt werden, beispielsweise Ligand-Rezeptor- und Molekül-Material-Wechselwirkungen. In diesen Bereichen hat die KI große Fortschritte bei der molekularen Charakterisierung und Generierung, der Molekulardynamik, der Vorhersage und dem Design von Proteinstrukturen, der Vorhersage von Materialeigenschaften und der Strukturgenerierung erzielt.
Großer Maßstab: Die Kontinuumsmechanik verwendet partielle Differentialgleichungen, um physikalische Prozesse zu modellieren, die sich zeitlich und räumlich auf makroskopischer Ebene entwickeln, einschließlich Flüssigkeitsströmung, Wärmeübertragung, elektromagnetische Wellen usw. KI-Methoden bieten einige Lösungen für Probleme wie die Verbesserung der Recheneffizienz, die Generalisierung und die Analyse mit mehreren Auflösungen.
1.2 KI-Technologiebereich
In mehreren Bereichen der wissenschaftlichen KI gibt es eine Reihe gemeinsamer technischer Herausforderungen.
**Symmetrie:**Symmetrie ist eine sehr starke induktive Paranoia, daher besteht eine zentrale Herausforderung für AI4Science darin, Symmetrie effektiv in KI-Modelle zu integrieren.
**Interpretierbarkeit:**Interpretierbarkeit ist in AI4Science von entscheidender Bedeutung, um die Gesetze der physischen Welt zu verstehen.
**Out-of-Distribution (OOD)-Generalisierung und Kausalität: **Um die Generierung von Trainingsdaten für jede unterschiedliche Einstellung zu vermeiden, müssen kausale Faktoren identifiziert werden, die eine OOD-Generalisierung ermöglichen.
**Grundlegende Modelle und große Sprachmodelle:**Grundlegende Modelle für Aufgaben zur Verarbeitung natürlicher Sprache werden unter selbstüberwachter oder verallgemeinerbarer Aufsicht vorab trainiert, um verschiedene nachgelagerte Aufgaben in wenigen oder null Schüssen auszuführen. Der Artikel bietet eine Perspektive darauf, wie dieses Paradigma die Entdeckungen von AI4Science beschleunigen kann.
**Unsicherheitsquantifizierung (UQ): **Untersucht, wie eine robuste Entscheidungsfindung unter Daten- und Modellunsicherheit sichergestellt werden kann.
**Bildung:** Um das Lernen und die Bildung zu erleichtern, stellt dieser Artikel eine kategorisierte Liste von Ressourcen bereit, die der Autor für nützlich hält, und bietet Perspektiven, wie die Community die Integration von KI in Wissenschaft und Bildung besser fördern kann.
**2. ** Symmetrie, Äquivarianz und ihre Theorien
Bei vielen wissenschaftlichen Problemen befindet sich das interessierende Objekt normalerweise im 3D-Raum, und jede mathematische Darstellung des Objekts basiert auf einem Referenzkoordinatensystem, wodurch eine solche Darstellung relativ zum Koordinatensystem erfolgt. Da es in der Natur jedoch keine Koordinatensysteme gibt, ist eine vom Koordinatensystem unabhängige Darstellung erforderlich. Daher besteht eine der größten Herausforderungen von AI4Science darin, wie man bei der Koordinatensystemtransformation Invarianz oder Äquivarianz erreicht.
2.1 Übersicht
Unter Symmetrie versteht man die Tatsache, dass die Eigenschaften eines physikalischen Phänomens bei bestimmten Transformationen, beispielsweise Koordinatentransformationen, unverändert bleiben. Wenn bestimmte Symmetrien im System vorhanden sind, ist das Vorhersageziel unter der entsprechenden Symmetrietransformation natürlich invariant oder äquivariant. Wenn Sie beispielsweise die Energie eines 3D-Moleküls vorhersagen, bleibt der vorhergesagte Wert unverändert, wenn das 3D-Molekül verschoben oder gedreht wird. Eine alternative Strategie zum Erreichen eines symmetriebewussten Lernens besteht darin, die Datenerweiterung beim überwachten Lernen zu verwenden, insbesondere durch die Anwendung zufälliger Symmetrietransformationen auf die Eingabedaten und Beschriftungen, um das Modell zu zwingen, annähernd äquivariante Vorhersagen auszugeben. Dies hat jedoch viele Nachteile:
1) Unter Berücksichtigung der zusätzlichen Freiheitsgrade bei der Auswahl des Koordinatensystems erfordert das Modell eine größere Kapazität zur Darstellung ursprünglich einfacher Muster in einem festen Koordinatensystem;
2) Viele Symmetrietransformationen, wie z. B. die Übersetzung, können eine unendliche Anzahl äquivarianter Stichproben erzeugen, was es für eine begrenzte Datenverbesserung schwierig macht, die Symmetrie in den Daten vollständig widerzuspiegeln;
3) In einigen Fällen ist es notwendig, ein sehr tiefes Modell zu erstellen, um gute Vorhersageergebnisse zu erzielen. Wenn nicht jede Schicht des Modells die Äquivarianz aufrechterhalten kann, ist es schwierig, die Gesamtausgabe der Äquivarianz vorherzusagen.
4) Bei wissenschaftlichen Problemen wie der molekularen Modellierung ist es entscheidend, eine Vorhersage zu liefern, die unter Symmetrietransformationen robust ist, damit maschinelles Lernen vertrauenswürdig eingesetzt werden kann.
Aufgrund der vielen Mängel der Datenerweiterung konzentriert sich die Forschung immer mehr auf die Entwicklung von Modellen für maschinelles Lernen, die Symmetrieanforderungen erfüllen. Unter der Symmetrieanpassungsarchitektur kann sich das Modell ohne Datenverbesserung auf die Aufgabe der Lernzielvorhersage konzentrieren.
2.2 Äquivariabilität unter diskreter Symmetrietransformation
In diesem Abschnitt liefert der Autor ein Beispiel für die Aufrechterhaltung der Äquivarianz bei diskreten Symmetrietransformationen in einem KI-Modell. Dieses Beispielproblem simuliert die Abbildung eines skalaren Strömungsfeldes in einer 2D-Ebene von einem Moment zum nächsten. Wenn sich das Eingabeflussfeld um 90, 180 und 270 Grad dreht, dreht sich auch das Ausgabeflussfeld entsprechend. Sein mathematischer Ausdruck lautet wie folgt:
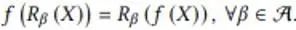
Dabei repräsentiert f die Flussfeld-Mapping-Funktion und R die diskrete Rotationstransformation. Cohen et al. schlugen äquivariante Gruppenfaltungs-Neuronale Netze (G-CNNs) vor, um dieses Problem zu lösen. Seine einfachste Grundkomponente ist die aufsteigende Faltung:
1) Drehen Sie zunächst den Faltungskern in allen Winkeln der symmetrischen Transformation und führen Sie mithilfe des gedrehten Faltungskerns entsprechende Faltungsoperationen an der Eingabe durch, um mehrere Merkmalsschichten zu erhalten, und stapeln Sie diese Merkmalsschichten in der neu generierten Rotationsdimension α Zusammen 2 ) Das Pooling wird in dieser Rotationsdimension α durchgeführt, sodass die resultierende Ausgabe eine entsprechende Drehung erzeugt, wenn die Eingabe X gedreht wird.
Aufgrund der Pooling-Operation können diese Merkmale keine Richtungsinformationen übertragen, obwohl die äquivalenten Zeilen beibehalten werden. Normalerweise übernehmen G-CNNs die in der folgenden Abbildung dargestellte Struktur:
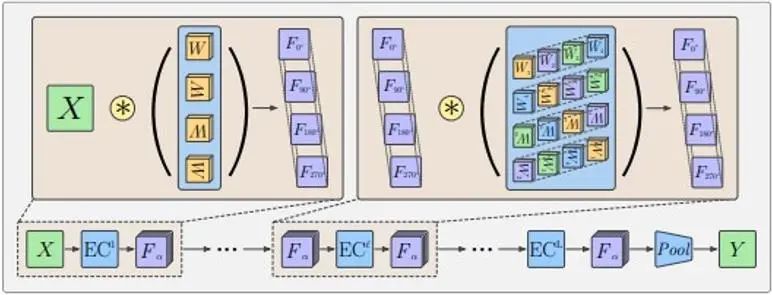
Zuerst wird ein Rotationsfaltungskern verwendet, um die Dimension der Eingabe zu erhöhen, dann wird eine mehrschichtige Gruppenfaltungsschicht verwendet, um sicherzustellen, dass jede Merkmalsschicht die Anforderungen der Rotationsäquivarianz erfüllt und gleichzeitig die Rotationsdimension beibehält, und schließlich wird eine Poolingschicht verwendet wird verwendet, um die Rotationsdimension zu eliminieren. Dadurch kann die Zwischen-Feature-Ebene Muster in relativen Positionen und Ausrichtungen von Features besser erkennen. Die Bedeutung der Äquivarianz der Zwischenmerkmalsschicht besteht darin, dass sich die Merkmalsschicht unter der Rotationstransformation entsprechend dreht und die Reihenfolge in der Rotationsdimension ebenfalls rotiert und die Rotation und das Rotationsdesign des Faltungskerns in der verwendeten Gruppenfaltungsschicht ebenfalls vorgenommen werden Die Ausgabe des Feature-Layers kann diese Äquivarianzcharakteristik beibehalten.
2.3-2.5 Konstruktion eines äquivarianten Modells der kontinuierlichen 3D-Transformation
Bei vielen wissenschaftlichen Problemen konzentrieren wir uns auf kontinuierliche Rotations- und Translationssymmetrien im 3D-Raum. Wenn sich beispielsweise die Struktur chemischer Moleküle dreht und verschiebt, erfährt der Vektor, der aus vorhergesagten molekularen Attributen besteht, entsprechende Transformationen. Diese kontinuierlichen Rotationstransformationen R und Translationstransformationen t bilden die Elemente in der SE(3)-Gruppe, und diese Transformationen können als Transformationsmatrizen im Vektorraum ausgedrückt werden. Die Transformationsmatrizen in verschiedenen Vektorräumen können unterschiedlich sein, diese Vektorräume können jedoch in unabhängige Untervektorräume zerlegt werden. In jedem Unterraum gelten die gleichen Transformationsregeln, das heißt, der Vektor, der durch Anwenden aller Transformationselemente in der Gruppe auf den Vektor des Unterraums erhalten wird, befindet sich immer noch im Unterraum Unterraum. Transformationsmatrixdarstellung. Beispielsweise bleiben Skalare wie Gesamtenergie und Energielücke unter der Wirkung von SE(3)-Gruppenelementen unverändert, und ihre Transformationsmatrix wird als D^0(R)=1 ausgedrückt; 3D-Vektoren wie Kraftfelder Die entsprechende Rotation erfolgt unter der Aktion, und ihre Transformationsmatrix wird als D^1(R)=R in einem höherdimensionalen Vektorraum ausgedrückt, D^l(R) ist ein 2l+1 -dimensionale quadratische Matrix. Diese Transformationsmatrizen D^l(R) werden als Wigner-D-Matrix l-Ordnung bezeichnet, die der Rotation R entspricht, und der entsprechende Untervektorraum wird zum irreduziblen invarianten Unterraum l-Ordnung der SE(3)-Gruppe Der darin enthaltene Vektor heißt äquivarianter Vektor l-Ordnung. Bei der Translationstransformation bleiben diese Vektoren immer unverändert, da sich die Eigenschaften, die uns interessieren, nur auf relative Positionen beziehen.
Der übliche Weg, dreidimensionale geometrische Informationen auf Merkmale im invarianten Unterraum der SE(3)-Gruppe abzubilden, ist die Verwendung der sphärischen harmonischen Funktionsabbildung. Die sphärische harmonische Funktion Y^l bildet einen dreidimensionalen Vektor in einen 2l+1-dimensionalen Vektor ab, der den Koeffizienten darstellt, wenn der Eingabevektor in 2l+1 grundlegende sphärische harmonische Funktionen zerlegt wird. Wie in der folgenden Abbildung dargestellt, wird die Deltafunktion auf der durch den dreidimensionalen Vektor dargestellten Kugel in gewissem Maße erweitert, da nur eine begrenzte Anzahl von Basen verwendet wird.

Sphärische Harmonische haben die folgenden äquivarianten Eigenschaften:
Unter diesen ist D die zuvor erwähnte Wigner-D-Matrix l-ter Ordnung. Daher wird eine Raumfunktion unter Rotationstransformation in eine Kombination äquivarianter Vektoren unterschiedlicher Ordnung zerlegt.
Unter der Annahme, dass in einem grafischen neuronalen Netzwerk mit Atomkoordinaten als Knoten das Knotenmerkmal h ein äquivarianter Vektor der Ordnung l_1 ist, kann durch die folgende Übertragung und Aktualisierung der Diagramminformationen sichergestellt werden, dass das aktualisierte h auch die Äquivarianz beibehält:
Der entscheidende Schritt dabei ist die Tensorproduktoperation (TP) bei der Informationsübertragung. Unter diesen bedeutet vec die Vektorisierung der Matrix, und der Koeffizient C ist eine Matrix mit 2l_3+1 Zeilen (2l_1+1) (2l_2+1) Spalten.
Das Knotenmerkmal h ist ein Vektor im irreduziblen invarianten Unterraum der Ordnung l_1. Die sphärische harmonische Funktion Y der Kantenrichtung r_ij ist ein Vektor im irreduziblen invarianten Unterraum der Ordnung l_2 Der Raum ist reduzierbar, und der Koeffizient C ist die Konvertierungsbeziehung von diesem reduzierbaren Raum in einen irreduziblen invarianten Unterraum der Ordnung l_3. Der direkte Produktraum zweier dreidimensionaler Vektoren lautet beispielsweise wie folgt:
Die Rotationstransformationsmatrix des direkten Produktraums kann in die Dreiblock-Diagonalmatrix in der Mitte der Abbildung oben umgewandelt werden, was bedeutet, dass dieser Raum in drei irreduzible invariante Unterräume mit den Dimensionen 1, 3 und 5 zerlegt werden kann. das heißt, 3⨂ Zerlegung des Vektorraums von 3=1⊕3⊕5. Der Koeffizient C ist die Transformationsmatrix von diesem neundimensionalen Raum in diesen eindimensionalen, dreidimensionalen bzw. fünfdimensionalen Raum. In der obigen Formel nehmen l_1, l_2 und l_3 alle nur einen Wert an und sind äquivariante Merkmale fester Ordnung. Die Merkmale im tatsächlichen Netzwerk können eine Kombination dieser Merkmale unterschiedlicher Ordnung sein.
2.6-2.7 In den vorherigen Beispielen wurden die Theorie der Gruppentheorie und die Eigenschaften sphärischer harmonischer Funktionen verwendet. Die Grundkenntnisse der Gruppentheorie und sphärischer harmonischer Funktionen werden in diesen beiden Kapiteln des Artikels ausführlich vorgestellt.
2.8 Der steuerbare Kernel stellt eine allgemeine Form eines äquivarianten Netzwerks dar
Die vorherigen äquivarianten Netzwerkschichten unter diskreten und kontinuierlichen Transformationen können in Form einer einheitlichen Variablenfaltung (steuerbares CNN) beschrieben werden:
Unter diesen sind x und y Raumkoordinaten, f_in(y) stellt den Eingabemerkmalsvektor an der Koordinate y dar, f_out(x) stellt den Ausgabemerkmalsvektor an der Koordinate x dar und K ist die Transformation vom Eingabemerkmalsraum zum Ausgabemerkmal Raum. Die Faltungsoperation stellt die translatorische Äquivarianz sicher. Um die Äquivarianz bei anderen räumlichen affinen Transformationen sicherzustellen, muss der Faltungskern K auch die folgenden Symmetriebeschränkungen erfüllen:
Unter diesen ist g die Transformation in der Raumtransformationsgruppe, und ρ_in und ρ_out repräsentieren die Darstellung der Transformation im Eingabe- bzw. Ausgabemerkmalsraum (d. h. der Transformationsmatrix).
An diesem Punkt ist die theoretische Erläuterung von Symmetrie und Äquivarianz des Artikels im Wesentlichen abgeschlossen, gefolgt von einem separaten Überblick über die in Kapitel 1 aufgeführten mehreren Felder.
Verweise
[1] Ren P, Rao C, Liu Y, et al. PhyCRNet: Physikinformiertes Faltungs-Rekurrent-Netzwerk zur Lösung raumzeitlicher PDEs[J]. Computermethoden in angewandter Mechanik und Ingenieurwesen, 2022, 389: 114399.
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
[1] Xuan Zhang, Limei Wang, Jacob Helwig, et al. 2023. Künstliche Intelligenz für die Wissenschaft in Quanten-, Atom- und Kontinuumssystemen. arXiv: https://arxiv.org/abs/2307.08423
[2] Taco Cohen und Max Welling. 2016. Gruppenäquivariante Faltungsnetzwerke. In der Internationalen Konferenz zum maschinellen Lernen. PMLR, 48:2990–2999.
[3] Nathaniel Thomas, Tess Smidt, Steven Kearnes, et al. 2018. Tensorfeldnetze: Rotations- und translatorisch äquivariante neuronale Netze für 3D-Punktwolken. arXiv: https://arxiv.org/abs/1802.08219
Maurice Weiler, Mario Geiger, Max Welling, et al. 2018. 3D-steuerbare CNNs: Lernen rotationsäquivarianter Merkmale in volumetrischen Daten. In Fortschritte in neuronalen Informationsverarbeitungssystemen
Ein in den 1990er Jahren geborener Programmierer hat eine Videoportierungssoftware entwickelt und in weniger als einem Jahr über 7 Millionen verdient. Das Ende war sehr bestrafend! Google bestätigte Entlassungen, die den „35-jährigen Fluch“ chinesischer Programmierer in den Flutter-, Dart- und Teams- Python mit sich brachten stark und wird von GPT-4.5 vermutet; Tongyi Qianwen Open Source 8 Modelle Arc Browser für Windows 1.0 in 3 Monaten offiziell GA Windows 10 Marktanteil erreicht 70 %, Windows 11 GitHub veröffentlicht weiterhin KI-natives Entwicklungstool GitHub Copilot Workspace JAVA ist die einzige starke Abfrage, die OLTP+OLAP verarbeiten kann. Dies ist das beste ORM. Wir treffen uns zu spät.