PSINS-Toolbox-Lernen (2) Konzept und Konvertierung von Haltungsmatrix, Quaternion, Euler-Winkel und äquivalentem Rotationsvektor

Die Haltung des Trägers bezieht sich auf die Orientierungsbeziehung zwischen dem Trägerkoordinatensystem und dem Navigationskoordinatensystem , und die direkte Orientierungsbeziehung zwischen den beiden Koordinatensystemen kann dem Problem der Festpunktrotation starrer Körper in der Mechanik entsprechen. In der Festpunktrotationstheorie starrer Körper gehören zu den traditionellen Methoden zur Beschreibung der Orientierungsbeziehung des sich bewegenden Koordinatensystems relativ zum Referenzkoordinatensystem die Euler-Winkel-Methode , die Richtungskosinus-Methode und die Quaternion-Methode . Sowohl die traditionelle Richtungskosinusmethode als auch die Quaternionmethode gehen davon aus, dass sich der Körper auf einer festen Achse bewegt, und in diesem Fall liegt kein Nichtkommutabilitätsfehler vor . Beim Strapdown-Trägheitsnavigationssystem ist das Trägheitsgerät jedoch direkt am Körper installiert und folgt der Bewegung des Körpers, sodass es für die tatsächliche Umgebung nicht geeignet ist, davon auszugehen, dass die Bewegung des Körpers eine feste Achse ist. Daher gilt: Für hochdynamische Umgebungen gibt es eine Haltungslösung mit höherer Genauigkeit. Berechnungsmethode: Äquivalente Rotationsvektormethode .

Da das Strapdown-Trägheitsnavigationssystem die durch die Berechnung der Lagematrix festgelegte mathematische Plattform übernimmt, hat der Lagealgorithmus im Aktualisierungsalgorithmus der Lage, Geschwindigkeit und Position des Strapdown-Trägheitsnavigationssystems den größten Einfluss auf die Genauigkeit des Ganzen System, und es ist der Kernpunkt der Algorithmusforschung und des Algorithmusdesigns .

Ziel der Lagelösung: Kennen Sie die anfänglichen Lageparameter und geben Sie die Lageparameter gemäß der Messung des Gyroskops in Echtzeit aus :

1. Grundkonzepte

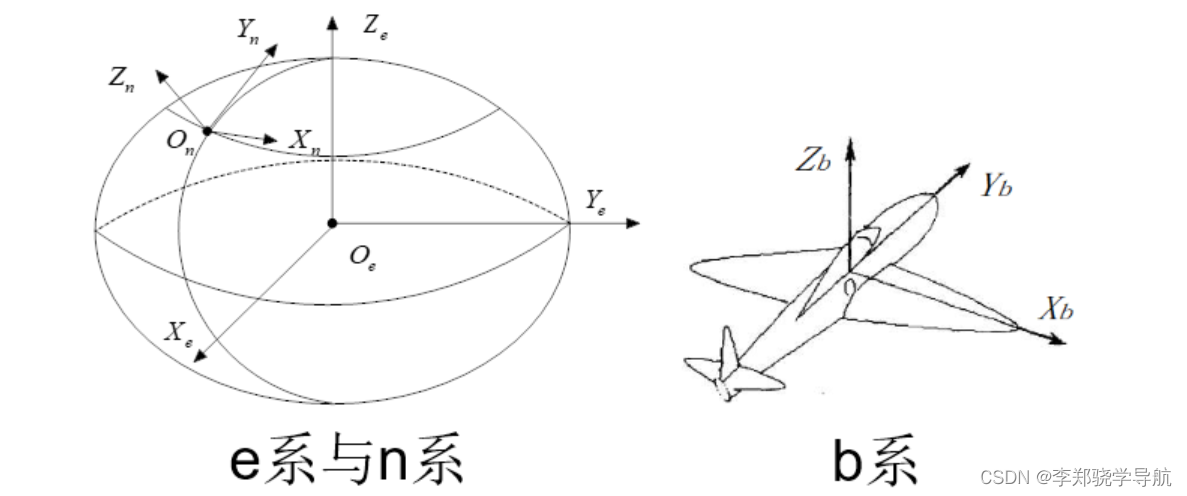
1. Definition des Koordinatensystems

Das Trägheitsnavigationskoordinatensystem kann entsprechend der Position und Achse des Ursprungs in vier Kategorien unterteilt werden:

1. Trägheitskoordinatensystem (i-System)

Auch als ECI bekannt, liegt der Ursprung im Massenmittelpunkt der Erde und die Koordinatenachse dreht sich nicht mit der Erde (die Z-Achse zeigt auf den Nordpol und die X-Achse zeigt auf die Frühlings-Tagundnachtgleiche). Darauf basiert die Ausgabe des Trägheitssensors. Obwohl es vom Gravitationsfeld der Sonne beeinflusst wird, gibt es $6\ast 10^{-7}g$orbitale Zentripetalkraft; wenn jedoch die Erde als Trägheitsnavigationsreferenz auf der Erdoberfläche verwendet wird, befinden sich der bewegte Träger und die Erde ungefähr im gleichen solaren Gravitationsfeld, und sein Einfluss kann ignoriert werden.

2. Erdzentriertes erdfestes Koordinatensystem (e-System)

Auch als ECEF bekannt, liegt der Ursprung im Massenmittelpunkt der Karte und die Koordinatenachse dreht sich mit der Erde (die Z-Achse zeigt auf den Nordpol und die X-Achse zeigt auf den Schnittpunkt von Äquator und Nullmeridian). ). Dieses Koordinatensystem wird am häufigsten von GNSS-Systemen verwendet. Die Winkelbewegung von ECEF relativ zu ECI ist die Winkelgeschwindigkeit der Erdrotation ${Oh}_{ich}$。

3. Navigationskoordinatensystem (n-System)

Auch als lokales horizontales Koordinatensystem bekannt. Der Ursprung liegt am Träger und die Koordinatenachse ändert sich nicht mit dem Träger . Es gibt zwei Beschreibungen: North East Earth (NED) und North East Heaven (ENU). Es ist das Koordinatensystem, das von der Trägheitsnavigation zur Lösung der Parameter verwendet wird. Bei der Berechnung der Trägheitsnavigation geht es insbesondere um die Erdbeschleunigung, die in diesem Koordinatensystem angezeigt werden kann.

4. Trägerkoordinatensystem (b-System)

Der Ursprung liegt am Träger und die Koordinatenachse ändert sich mit dem Träger . Im Vergleich zum Navigationskoordinatensystem gibt es auch zwei Beschreibungen: vorne unten rechts (FRD) und rechts vorne oben (RFU). Es gibt viele B-Serien in einem Navigationssystem: B-Serie von IMU, B-Serie von Trägern, B-Serie von Kameras und so weiter. Die Azimutbeziehung zwischen B-System und I-System kann durch einen Satz Euler-Winkel beschrieben werden.

In PSINS: Navigationskoordinatensystem (n): Ost E-Nord N-Tag U, Fahrzeugkoordinatensystem (b): rechts R-vorne F-oben U

2. Antisymmetrisches Array

$$(V\times )=\left[\begin{array}{ccc}0& -V_{}& V_{}\\ V_{}& 0& -V_{}\\ -V_{}& V_{}& \end{array}\right]$$

Antisymmetriepunkte::

1. Beide sind auf der Diagonale 0 und der obere und untere Teil sind symmetrisch und entgegengesetzt, das heißt: $(V\times )=-(V\times {)}^T$ , daher spricht man von einer antisymmetrischen Matrix.

2. Das Kreuzprodukt eines Vektors mit einem anderen Vektor ist gleich dem Punktprodukt der antisymmetrischen Matrix eines anderen Vektors, und das Kreuzprodukt wird in ein Punktprodukt umgewandelt .

3. 反对称阵的幂方通式:
   $$(V\times {)}^{ich}=\{\begin{array}{ll}(-1{)}^{(i-1)/2}{v}^{i-1}(V\times )& ich=1,3,5,\cdots \\ (-1{)}^{(i-2)/2}{v}^{i-2}(V\times {)}^{}& ich=2,4,6,\end{array}$$

3. Euler-Winkel

$$A={\left[\begin{array}{lll}& & \end{array}\right]}^T$$

Der Euler-Winkel ist eine klassische Methode zur Beschreibung der relativen Lage zwischen zwei Koordinatensystemen durch den um die Koordinatenachse transformierten Winkel . Die physikalische Bedeutung ist intuitiv und leicht zu verstehen, insbesondere zur Beschreibung der Bewegung des Trägerkoordinatensystems relativ zur lokalen Navigationskoordinate System .

Euler-Winkel stellen Rotation dar : Im dreidimensionalen Raum kann die Orientierungsbeziehung eines rechteckigen Koordinatensystems relativ zu einem anderen rechteckigen Koordinatensystem durch drei aufeinanderfolgende Drehungen beschrieben werden , und die Koordinatenachse um jede Drehung ist orthogonal zur vorderen und hinteren Rotationsachse. Euler hat bewiesen, dass die relative Orientierungsbeziehung zwischen zwei beliebigen orthogonalen Koordinatensystemen durch einen Satz von Winkeln von mindestens 3 beschrieben werden kann und die Drehwinkel dieser drei Drehungen als Satz von Euler-Winkeln (Euler-Winkelgruppe) bezeichnet werden .

Euler-Winkel stellen die Lage dar : Um die Lage des Trägers zu beschreiben, können Sie ein Referenzkoordinatensystem angeben und dann einen Satz Euler-Winkel verwenden, um die Drehung des Koordinatensystems, das mit dem Träger und dem Festkörper verbunden ist, relativ zu beschreiben Referenzkoordinatensystem. Bei erdnahen Navigationsanwendungen wählt das Referenzkoordinatensystem im Allgemeinen standardmäßig das lokale geografische Koordinatensystem aus, während das bewegliche Koordinatensystem ein fest mit dem Fahrzeug verbundenes Koordinatensystem ist.

• Kurswinkel : Der Winkel zwischen der Projektion der positiven Längsachse des Trägers auf die lokale horizontale Ebene und der lokalen geografischen Nordrichtung. Er wird oft als positiv von Nord nach Ost angenommen, im Allgemeinen dargestellt durch ψ, und der Winkelbereich beträgt 0 ∼ 360◦ oder −180◦ ∼ +180◦ .
• Neigungswinkel : Der Winkel zwischen der positiven Richtung der Längsachse des Trägers und seiner horizontalen Projektionslinie. Er wird als positiv definiert, wenn der Träger „seinen Kopf hebt“, im Allgemeinen dargestellt durch θ, und sein Wert liegt im Bereich von –90◦ bis 90◦.
• Rollwinkel : Der Winkel zwischen der positiven Richtung der vertikalen Achse des Trägers und der vertikalen Ebene, in der sich die Längsachse des Trägers befindet. Wenn der Träger nach rechts neigt (z. B. wenn der rechte Flügel des Flugzeugs nach unten gedrückt wird) , es ist positiv. Verwenden Sie ϕ \ $\varphi$ gibt an, dass der Wertebereich −180◦ ∼ +180◦ beträgt.

Grundlagen der Eulerschen Winkel::

1. Die relative Orientierungsbeziehung zwischen zwei orthogonalen Koordinatensystemen kann durch einen Satz Euler-Winkel beschrieben werden. Bei einem Satz Euler-Winkel muss gleichzeitig die entsprechende Rotationsachsenreihenfolge angegeben werden. PSINS verwendet den Nordosthimmel, 312 Euler-Winkel
2. Der Navigationslagewinkel, einschließlich Kurswinkel, Nickwinkel und Rollwinkel, hängt eng mit der physischen Achse des Fahrzeugs zusammen und hat nichts mit dem ausgewählten mathematischen Koordinatensystem des Fahrzeugs zu tun.
3. Wenn der Steigungswinkel $\pm 90^{Wenn\; \circ }$ , gibt es einen singulären Wert in der Euler-Winkeltransformation, und der Rollwinkel und der Kurswinkel können derzeit nicht unterschieden werden. Daher kann die Euler-Winkelmethode nicht für Navigationsanwendungen in voller Flughöhe verwendet werden.
4. Sätze von Euler-Winkeln können nicht direkt addiert werden, um die Zusammensetzung zweier Rotationen darzustellen.

4. Rotationsmatrix/Richtungskosinusmatrix

$$C=\left[\begin{array}{lll}{C}_{}& C_x& C_x\\ C_y& C_{}& C_{}\\ C_z& C_{}& C_{}\end{array}\right]$$

Die Richtungskosinusmatrix (Direction Cosine Matrix, DCM) ist eine Lagematrix, die durch den Richtungskosinus des Vektors dargestellt wird und häufig zur Beschreibung der relativen Lage zweier Koordinatensysteme verwendet wird. Im Vergleich zum Euler-Winkel ist die Richtungskosinusmatrix viel abstrakter, aber die Projektionstransformation von Vektoren ist sehr praktisch .

Wir wissen, dass die drei Projektionswerte des Vektors im Raum die Koordinaten sind und derselbe Vektor in $i$ -Serie und$Das\; b-$ System hat zwei Koordinatensätze und ihre Beziehung kann ausgedrückt werden als:
$$V=V_X^{}{ich}_{}+V_j^{}{J}_{}+V_z^{}{k}_{}=V_X^{}{ich}_{}+V_j^{}{J}_{}+V_z^{}{k}_{}$$
即$\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]\left[\begin{array}{c}{V}_X^{}\\ V_j^{}\\ V_z^{}\end{array}\right]=\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]\left[\begin{array}{c}{V}_X^{}\\ V_j^{}\\ V_z^{}\end{array}\right]=\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]P\left[\begin{array}{c}{V}_X^{}\\ V_j^{}\\ V_z^{}\end{array}\right]$

有:
$$\left[\begin{array}{c}{V}_X^{}\\ V_j^{}\\ V_z^{}\end{array}\right]=P\left[\begin{array}{c}{V}_X^{}\\ V_j^{}\\ V_z^{}\end{array}\right]$$
记为$V^{ich}=P{V}^B=C_B^{}{V}^b$，$C_B^{}$Sie wird als Koordinatensystemtransformationsmatrix (i->b) oder Koordinatentransformationsmatrix (b->i) bezeichnet, auch bekannt als Richtungskosinusmatrix und Übergangsmatrix .

Grundlagen des Richtungs-Kosinus-Arrays::

1. Da es sich bei allen um Einheitsarrays handelt, stellt jedes Element im Richtungskosinusarray den Kosinuswert des Winkels zwischen den Koordinatenachsen der beiden Sätze von Koordinatensystemen dar, daher der Name.
2. Unterscheiden Sie zwischen der Koordinatensystemtransformationsmatrix und der Koordinatentransformationsmatrix .
3. Obwohl das Richtungskosinus-Array 9 Parameter hat, enthält es 6 Einschränkungen, das heißt, der Modul des Zeilenvektors beträgt 1 und jedes Paar ist orthogonal und nur 3 Parameter sind unabhängig.
4. Die Richtungskosinusmatrix ist eine orthogonale Matrix , ${\left(C_A^{}\right)}^{-1}={\left(C_A^{}\right)}^{T.}$ _ Mehrere aufeinanderfolgende Rotationen können durch Multiplikation entsprechender Kosinusmatrizen mit mehreren Richtungen dargestellt werden:$C_A^{}=C_B^{}{C}_A^{}$。
5. Wenn sich der Träger bewegt, ändert sich die relative Lage zwischen den beiden Koordinatensystemen mit der Zeit und die entsprechende Richtungskosinusmatrix $C_B^{}\left(t\right)$ ist eine zeitveränderliche Matrix und ihre Differentialgleichung lautet${\dot{C}}_B^{}=C_B^{}\left({oh}_{Rb}^{}\times \right)$。
6. Die Picard-Iterationsmethode kann verwendet werden , um die Differentialgleichung der Richtungskosinusmatrix zu lösen, und man erhält eine Reihe, die durch ein unendlich wiederholtes Integral dargestellt wird, die auch Picard-Reihe genannt wird. Die obige Reihe ist geschlossen, aber nur in der „festen“ Form Achsendrehung " Nur in einem Sonderfall kann die geschlossene Lösung der folgenden Form erhalten werden: $C_B^{}\left(t\right)=C\left(0\right)\exp \left({\int }_0^{}\Omega \left(\tau \right)d\tau \right)$ .
7. 姿态手机公式: $C_{b\left(k\right)}^{}=C_{b(k-1)}^i{\mathbf{C}}_{b(k)}^{b(k-1)}$，${\mathbf{C}}_{b(k)}^{b(k-1)}=\mathbf{I}+\frac{\sin \Delta {\theta }_k}{\Delta {\theta }_k}\left[\Delta {\mathbf{\theta }}_k\times \right]+\frac{1-\cos \Delta {\theta }_k}{\Delta {\theta }_k^2}{\left[\Delta {\mathbf{\theta }}_k\times \right]}^2$
8. Für gängige Trägheitsnavigationsanwendungen, $Die\; Annahme\; einer\; festen\; Achsenrotation\; des\; B$ -Systems ist im Allgemeinen nicht gültig. Wenn diese Bedingung nicht erfüllt ist, wird das vom Kreisel ausgegebene Winkelinkrement weiterhin auf die Formel für die rekursive Berechnung der Lageaktualisierung angewendet, was zu einem führtDas irreversible Problem bei der Lösung der Einstellungsaktualisierung. Sexueller Fehler,der äquivalente Rotationsvektor kann zur Lösung dieses Problems verwendet werden.

5. Quaternionen

$$Q=Q_{}+Q_{}ich+Q_{}J+Q_{}k=Q_{}+Q_{}$$

Wir wissen, dass komplexe Zahlen als Vektoren auf der komplexen Ebene, also als zweidimensionale Vektoren, betrachtet werden können. Durch Erweiterung des Konzepts komplexer Zahlen können Quaternionen erhalten werden, um Vektoren im dreidimensionalen Raum zu beschreiben.

Quaternion-Grundlagen::

1. Quaternionen haben hauptsächlich die folgenden Darstellungen: $Q=Q_{}+Q_{}ich+Q_{}J+Q_{}k$ , Vektorkoordinatenform$Q={\left[q_{},Q_{},Q_{},Q_{}\right]}^T$、$Q=Q_{}+Q_{}$Oder die trigonometrische Form $Q=\cos \frac{}{2}+u\mathrm{Sünde}\frac{}{2}$(Bezogen auf den äquivalenten Rotationsvektor, normalisiert, beträgt der Modul eins)

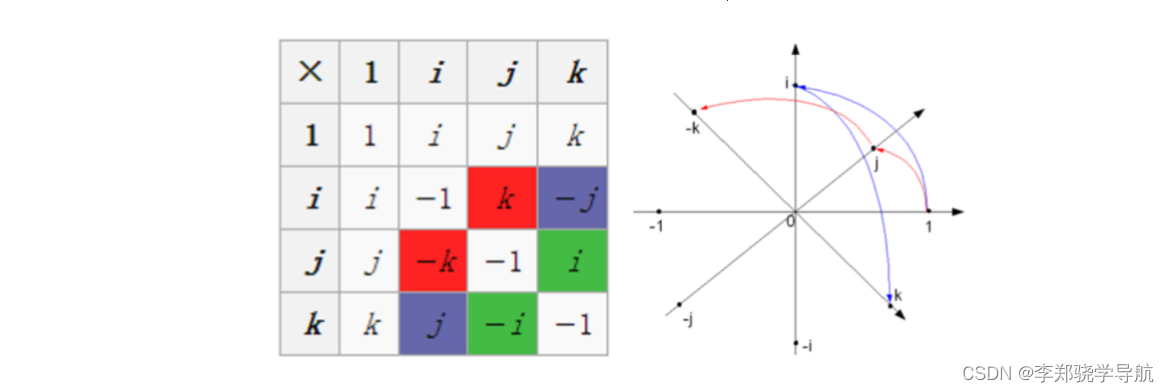
2. Die Multiplikation zwischen imaginären Einheiten einer Quaternion weist die folgenden Merkmale auf: Wenn die Einheit mit sich selbst multipliziert wird, ist die Leistung dieselbe wie bei komplexen Zahlen, und die Multiplikation zwischen zwei Paaren ist dieselbe wie das äußere Produkt (Kreuzprodukt) von drei -dimensionale Vektoren.
   $$\{\begin{array}{l}ich\circ ich=J\circ J=k\circ k=-1\\ ich\circ J=k,J\circ k=ich,k\circ ich=j,J\circ ich=-k,k\circ J=-ich,ich\circ k=-\end{array}$$

3. Die Koordinatentransformation des dreidimensionalen Vektors kann mithilfe des Rotationstransformationsoperators der Quaternion realisiert werden: $v^R=Q_B^{}\circ v^B\circ Q_B^{R^{}}$。

4. Trigonometrische Notation der Einheitsquaternion : $Q=Q_{}+Q_{}=\cos \frac{}{2}+u\mathrm{Sünde}\frac{}{2}$hat eine klare physikalische Bedeutung. Rechts von der Quaternion wird häufig ein Index hinzugefügt, geschrieben als $Q_B^{}$，中$u$ stellt das bewegte Koordinatensystem dar ($b-$ System) relativ zum Referenzkoordinatensystem ($i$ -System) die Einheitsdrehachse,$\varphi$ gibt die Größe des Drehwinkels an,$\varphi u$ stellt den äquivalenten Rotationsvektor dar. Nach der Verwendung von Indizes kann die konjugierte Quaternion wie folgt geschrieben werden:$Q_{ich}^{}={\left(Q_B^{}\right)}^{\ast }$ , was der Darstellung der Matrixtransposition ähnelt, wie etwa$C_{ich}^{}={\left(C_B^{}\right)}^{T.}$ _

5. Differentialgleichung für Quaternionen: $Q_B^{}=\frac{}{2}{Q}_B^{}\circ \left[\begin{array}{c}0\\ {Oh}_{Rb}^{}\end{array}\right]$ , oder in Matrixform:$Q_B^{}=\frac{}{2}W{q}_B^{}$. Damit wird der Zusammenhang zwischen dem Quaternion und der Rotationswinkelgeschwindigkeit hergestellt.

6. Lösen Sie Differentialgleichungen für Quaternionen, wenn $Wenn\; das\; System\; b$ die Bedingung der „Rotation fester Achse“ erfüllt, kann die analytische Lösung erhalten werden:$Q_B^{}\left(t\right)=$ $\left[Ich\cos \frac{D}{2}+\frac{}{Di}\mathrm{Sünde}\frac{D}{2}\right]Q_B^{}\left(0\right)$。

7. Es gibt auch Oktonionen, die zur Beschreibung von Spiralbewegungen, Drahtbewegungen und Winkelbewegungen verwendet werden.

6. Äquivalenter Rotationsvektor

Euler schlug erstmals das Konzept des äquivalenten Rotationsvektors vor, als er die Bewegung starrer Körper untersuchte. Er wies darauf hin, dass jede endliche Fixpunktrotation eines starren Körpers äquivalent durch eine Drehung um eine Achse realisiert werden kann, die durch den Fixpunkt verläuft . Und die Transformationsformel des Einheitsvektors auf dem starren Körper vor und nach der Drehung wird erstellt. Der Schlüssel zur Erforschung des modernen Strapdown-Trägheitsnavigations- Lageaktualisierungsalgorithmus liegt darin, wie der Messwert des Gyroskops verwendet werden kann, um den entsprechenden äquivalenten Rotationsvektor zu konstruieren , um den nicht austauschbaren Fehler im Lageaktualisierungsalgorithmus zu minimieren oder zu beseitigen . Die anschließende Verwendung des äquivalenten Rotationsvektors zur Berechnung der Lageänderung, beispielsweise ausgedrückt durch eine Richtungskosinusmatrix oder eine Quaternion, wird sehr einfach.

Verwenden Sie die Abtastwerte mehrerer Winkelinkremente, um einen äquivalenten Rotationsvektor gemäß verschiedenen Beispielalgorithmen zu berechnen, und verwenden Sie dann den berechneten äquivalenten Rotationsvektor, um die Richtungskosinusmatrix und die Quaternion zu aktualisieren.

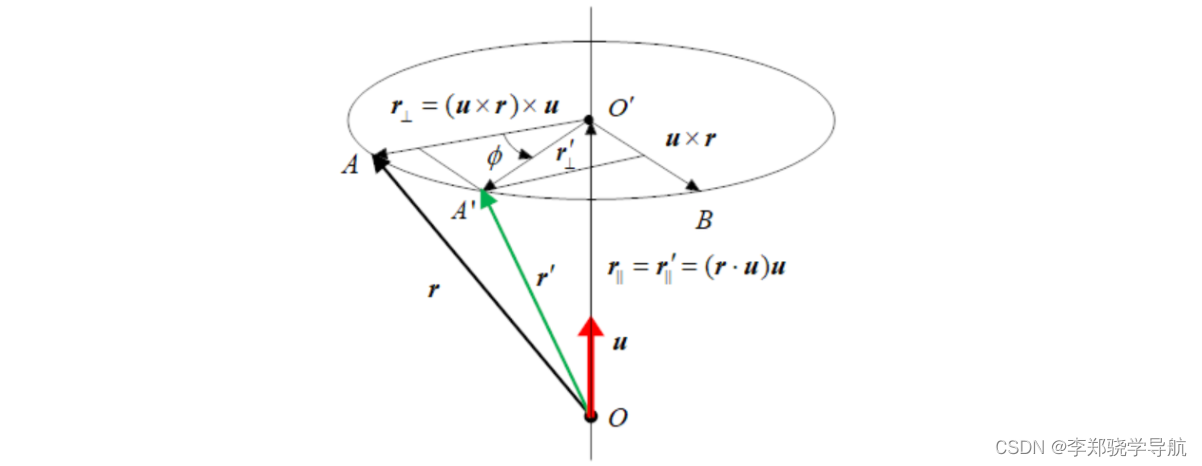
Raumvektor $r$ Rotationsachsenvektor$u$ rotiere$\varphi$ , der durch Rotation erhaltene$R^{{}^{\text{'}}}$ . Die vier Größen müssen direkt einen funktionalen Zusammenhang haben$R^{{}^{\text{'}}}=f(r,du,\varphi )$ ,利用一些几何关系，可以推导得到:
$$\begin{array}{rl}{R}^{\text{'}}& =(u\cdot \mathbf{r})\mathbf{u}+(\mathbf{u}\times \mathbf{r})\times \mathbf{u}\cos \varphi +\mathbf{u}\times \mathbf{r}\sin \varphi \\ & =\left[\mathbf{I}+(\mathbf{u}\times {)}^2\right]\mathbf{r}-(\mathbf{u}\times {)}^2\mathbf{r}\cos \varphi +\mathbf{u}\times \mathbf{r}\sin \varphi \\ & =\left[\mathbf{I}+\sin \varphi (\mathbf{u}\times )+(1-\cos \varphi )(\mathbf{u}\times {)}^2\right]\mathbf{r}=\mathbf{D}\mathbf{r}\end{array}$$
可记 $\mathbf{D}=\mathbf{I}+\sin \varphi (\mathbf{u}\times )+(1-\cos \varphi )(\mathbf{u}\times {)}^2$ ，此公式称为罗德里格旋转公式；$r^{\prime }$ 转到 $r$ 中间乘的矩阵称为罗德里格旋转矩阵，和转轴$u$ 及转角 $\varphi$ hängt zusammen.

Durch Anwendung der Rotationsformel von Rodrigue auf die Einheitskoordinatenachse des kartesischen Koordinatensystems kann das Referenzkoordinatensystem auf das bewegte Koordinatensystem übertragen werden:
ib = D iijb = D jikb = D ki } \left.\begin{array}{c} \boldsymbol{i}_{b}=\boldsymbol{D} \boldsymbol{i}_{i} \\ \boldsymbol{j}_{b}=\boldsymbol{D} \boldsymbol{j}_{i} \ \ \boldsymbol{k}_{b}=\boldsymbol{D} \boldsymbol{k}_{i}\end{array}\right\}ichb=Sag _ichJb=Dj _ichkb=D kich​⎭ ⎬ ⎫

$$\{\begin{array}{c}Beziehung\; zur\; Basisrotationstransformation:\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]=D\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]\\ Basisprojektionstransformationsbeziehung:\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]=\left[\begin{array}{lll}{ich}_{}& J_{}& k_{}\end{array}\right]\end{array}$$

$$Projektionimi-\; System:\begin{array}{l}\left[\begin{array}{lll}{ich}_B^{}& J_B^{}& k_B^{}\end{array}\right]=D\left[\begin{array}{lll}{ich}_{ich}^{}& J_{ich}^{}& k_{ich}^{}\end{array}\right]=DI\\ \left[\begin{array}{lll}{ich}_B^{}& J_B^{}& k_B^{}\end{array}\right]=\left[\begin{array}{lll}{ich}_{ich}^{}& J_{ich}^{}& k_{ich}^{}\end{array}\right]P=\end{array}\}D=P=C_B^{}$$

$P=D$ zeigt, dass die Rodrigue-Rotationsmatrix$D$ ist genau vom Referenzrahmen ($i$ -System) zum bewegten Koordinatensystem ($b$ -Reihe) Übergangsmatrix, die ebenfalls aus$b$ bisiiDie Koordinatentransformationsmatrix des$i-\; Systems.$Daher kann die Rodrigue-Rotationsformel in Form einer Richtungsmatrix umgeschrieben werden:
$$C_B^{}=ICH+\mathrm{Sünde}\varphi (u\times )+(1-\cos \varphi )(u\times {)}^2$$
Wenn außerdem Datensatz$\varphi =\varphi u$和$\varphi =|\varphi |$ , dann$u=\varphi /\varphi$，得：
$$C_B^{}=ICH+\frac{\mathrm{Sünde}}{\varphi }(\varphi \times )+\frac{1-\cos }{{\varphi }^2}(\varphi \times {)}^{2Hier}$$ ϕ \boldsymbol{\phi
}$\varphi$ heißtäquivalenter Rotationsvektor(RV, auch Rotationsvektor genannt)

Äquivalente Rotationsvektor-Grundlagen::

1. Endliche Drehungen starrer Körper sind nicht kommutativ. Eine endliche Fixpunktrotation eines starren Körpers kann durch eine Drehung um eine Achse realisiert werden, die durch den Fixpunkt verläuft.
2. Seine Vektorrichtung stellt die Drehrichtung dar, und die Größe des Moduls stellt die Größe des Drehwinkels dar.
3. 当载体的角速度方向随时间变化而不是做 “定轴转动” 时, 直接将传感器角增量测量值代入方向余弦矩阵或四元数微分方程的求解计算式中，则会带来 “不可交换性误差”。
4. Bortz 方程： $\dot{\varphi }=\mathbf{\omega }+\frac{1}{2}(\varphi \times \omega )+\frac{1}{{\varphi }^2}\left[1-\frac{\varphi \sin \varphi }{2(1-\cos \varphi )}\right]\mathbf{\varphi }\times (\mathbf{\varphi }\times \mathbf{\omega })$ 。是一种常用的等效旋转矢量微分方程，利用等效旋转矢量进行转动不可交换误差补偿。
5. 等效旋转矢量的双子样求解式：${\varphi }_k=\Delta {\theta }_k+\frac{1}{12}\Delta {\theta }_{k-1}\times \Delta {\theta }_k$ 。

二、PSINS中的表示转换

1、姿态阵/姿态四元数/欧拉角的表示 Cnb/qnb/att

• 有角标的符号书写一般遵从规律是从左到右从上到下。

• 姿态阵：Cnb，表示从 b 系到 n 系的坐标变换矩阵。对应姿态四元数写为qnb。

• 欧拉角：att=[俯仰pitch; 横滚roll; 方位yaw]。没有按照转到顺序来写，如果按转动顺序，东北天坐标系转到右前下坐标系，常见先转方位角、然后俯仰角、横滚角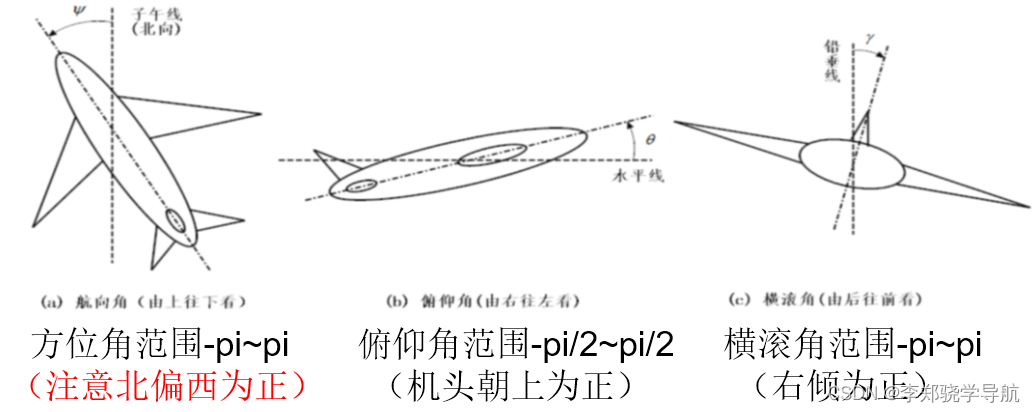

  

2、四元数计算

1. 四元数共轭：qconj

实部不变，虚部取反。

function qo = qconj(qi)
    qo = [qi(1); -qi(2:4)];

性质：

• 加的共轭等于共轭的加：$(\mathbf{P}+Q{)}^{\ast }=P^{\ast }+Q^{\ast }$
• 乘的共轭等于共轭的和：$(\mathbf{P}\circ Q{)}^{\ast }=Q^{\ast }\circ P^{\ast }$

2. 四元数归一化：qconj

function qnb = qnormlz(qnb)
    qnb = qnb/norm(qnb);

3. Quaternion-Multiplikation: qmual

$$\{\begin{array}{l}ich\circ ich=J\circ J=k\circ k=-1\\ ich\circ J=k,J\circ k=ich,k\circ ich=j,J\circ ich=-k,k\circ J=-ich,ich\circ k=-\end{array}$$

Der Wechselkurs wird nicht eingehalten. $Die\; Vorwärtsmultiplikation\; von\; i,j,k$ ist gleich dem letztgenannten Element, und das negative Vorzeichen sollte zur Rückwärtsmultiplikation hinzugefügt werden.

function q = qmul(q1, q2)
    if length(q2)==3, q2=[0; q2]; end  % 0-scale quaternion
    q = [ q1(1) * q2(1) - q1(2) * q2(2) - q1(3) * q2(3) - q1(4) * q2(4);
          q1(1) * q2(2) + q1(2) * q2(1) + q1(3) * q2(4) - q1(4) * q2(3);
          q1(1) * q2(3) + q1(3) * q2(1) + q1(4) * q2(2) - q1(2) * q2(4);
          q1(1) * q2(4) + q1(4) * q2(1) + q1(2) * q2(3) - q1(3) * q2(2) ];

AI-Erklärung :
Diese Funktion implementiert die Multiplikationsoperation zweier Quaternionen. Eine Quaternion ist ein mathematisches Objekt, das zur Darstellung von Rotationen und affinen Transformationen verwendet wird. In dieser Funktion sind q1 und q2 zwei Quaternionen, die Funktion multipliziert sie und speichert das Ergebnis in der Variablen q.

1. Zunächst prüft die Funktion, ob die Länge von q2 3 beträgt. Wenn ja, wird q2 zu einer Quaternion der Länge 4 erweitert, wobei ein Element auf 0 gesetzt ist. Dadurch soll bei nachfolgenden Berechnungen eine Division durch 0 vermieden werden.
2. Als nächstes berechnet die Funktion das Ergebnis mithilfe der Multiplikationsformel für Quaternionen. Die Multiplikation von Quaternionen kann durch entsprechende Multiplikation der Komponenten zweier Quaternionen und anschließende Addition der Produkte erreicht werden.
3. Abschließend speichert die Funktion das berechnete Ergebnis in der Variablen q und gibt diese Variable als Funktionsausgabe zurück.

4. Quaternion-Multiplikationsvektor (Koordinatentransformation eines dreidimensionalen Vektors): qmulv

Unter der Annahme eines 3D-Vektors $r$ , im Trägerkoordinatensystem ($b-$ System) und Referenzkoordinatensystem (iiDie Projektionen im$i-$$R^B={\left[\begin{array}{lll}{R}_X^{}& R_j^{}& R_z^{}\end{array}\right]}^T$和$R^{ich}={\left[\begin{array}{lll}{R}_X^{}& R_j^{}& R_z^{}\end{array}\right]}^T$ , nun für den Vektor$R^b$ (als nullskalare Quaternion behandelt) implementiert die folgende Quaternion-Multiplikationsoperation:
$$\begin{array}{rl}{Q}_B^{}\circ R^B\circ Q_{ich}^{}=& M_{Q_B^{}}\left(r^B\circ Q_{ich}^{}\right)=M_{Q_B^{}}\left(M_{Q_{ich}^{}}^{}\left[\begin{array}{c}0\\ R^{}\end{array}\right]\right)=M_{Q_B^{}}{M}_{Q_{ich}^{}}^{}\left[\begin{array}{c}0\\ R^{}\end{array}\right]=\\ & \left[\begin{array}{cccc}{Q}_{}& -q_{}& -q_{}& -q_{}\\ Q_{}& Q_{}& -q_{}& Q_{}\\ Q_{}& Q_{}& Q_{}& -q_{}\\ Q_{}& -q_{}& Q_{}& Q_{}\end{array}\right]\left[\begin{array}{cccc}{Q}_{}& Q_{}& Q_{}& Q_{}\\ -q_{}& Q_{}& -q_{}& Q_{}\\ -q_{}& Q_{}& Q_{}& -q_{}\\ -q_{}& -q_{}& Q_{}& Q_{}\end{array}\right]\left[\begin{array}{c}0\\ R_X^{}\\ R_j^{}\\ R_z^{}\end{array}\right]=\\ & \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& Q_0^{}+Q_1^{}-Q_2^{}-Q_3^{}& 2\left(q_{}{Q}_{}-Q_{}{Q}_{}\right)& 2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)\\ 0& 2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)& Q_0^{}-Q_1^{}+Q_2^{}-Q_3^{}& 2\left(q_{}{Q}_{}-Q_{}{Q}_{}\right)\\ & 2(q_{}{Q}_{}-Q_{}{Q}_{}& 2(q_{}{Q}_{}+Q_{}{Q}_{}& Q_0^{}-Q_1^{}-Q_2^{}+Q_3^{}\end{array}\right]\left[\begin{array}{c}0\\ R_X^{}\\ R_j^{}\\ R_z^{}\end{array}\right]\end{array}$$
Es kann festgestellt werden, dass die Diagonalblockmatrix dritter Ordnung in der unteren rechten Ecke der Matrix genau die Einstellungsmatrix ist, die wie folgt abgekürzt werden kann:
$$Q_B^{}\circ R^B\circ Q_{ich}^{}=\left[\begin{array}{cc}1& 0_{1\times }\\ 0_{3\times }& C_B^{}\end{array}\right]\left[\begin{array}{c}0\\ R^{}\end{array}\right]=\left[\begin{array}{c}0\\ C_B^{}{R}^{}\end{array}\right]=\left[\begin{array}{c}0\\ R^{}\end{array}\right]$$
Dies zeigt, dass$Q_B^{}\circ R^B\circ Q_{ich}^{}$Das Ergebnis ist ebenfalls eine nullskalare Quaternion, deren Imaginärteil genau der Koordinatentransformation $R^{ich}=C_B^{}{R}^b$ . Um prägnant zu schreiben, kann ähnlich wie bei der Koordinatentransformationsausdrucksgewohnheit der Matrix die Multiplikationsoperation zwischen der Quaternion und dem dreidimensionalen Vektor definiert werden, dh die Quaternionkoordinatentransformationsformel: ri = Q bi ⊗ rbr^{ i}
$$R^{ich}=Q_B^{}\otimes R^{Die\; Bedeutung\; von\; b}$$
besteht darin, zuerst eine Quaternion-Multiplikation durchzuführen und dann den Imaginärteil des Ergebnisses zu extrahieren.

function vo = qmulv(q, vi)
    qo1 =              - q(2) * vi(1) - q(3) * vi(2) - q(4) * vi(3);
    qo2 = q(1) * vi(1)                + q(3) * vi(3) - q(4) * vi(2);
    qo3 = q(1) * vi(2)                + q(4) * vi(1) - q(2) * vi(3);
    qo4 = q(1) * vi(3)                + q(2) * vi(2) - q(3) * vi(1);
    vo = vi;
    vo(1) = -qo1 * q(2) + qo2 * q(1) - qo3 * q(4) + qo4 * q(3);
    vo(2) = -qo1 * q(3) + qo3 * q(1) - qo4 * q(2) + qo2 * q(4);
    vo(3) = -qo1 * q(4) + qo4 * q(1) - qo2 * q(3) + qo3 * q(2);

5. Quaternion plus Fehlausrichtungswinkelfehler: qaddphi

Vom echten Navigationssystem ( $n$ -System) zum rechnerischen Navigationssystem ($N^{\prime }$ -System) beträgt der Fehlausrichtungswinkel$\varphi$ umgekehrt aus$N^{\text{'}}$ ist annnDer Fehlausrichtungswinkel des$n-$$-\varphi$ , wenn$-\varphi$ wird als äquivalenter Rotationsvektor betrachtet, dann ist die entsprechende Transformationsquaternion$Q_N^{N^{}}$. Im Programm repräsentieren die Variablen qpb, , Q bn ′ , Q bn Q_{b}^{n^{\prime}} bzw. Q_{b}^{n}qnbphi$Q_B^{N^{}},Q_B^{}$und $\varphi$ .

function qpb = qaddphi(qnb, phi)
    qpb = qmul(rv2q(-phi),qnb);

6. Quaternion minus Fehlausrichtungsfehler: qdelphi

Entsprechend der Formel $Q_B^{}=Q_{N^{\text{'}}}^{}{}^{\circ }{F}_B^{}$, was bedeutet: Nach Abzug des Fehlausrichtungswinkels bei der Berechnung der Lagequaternion erhält man die tatsächliche (genauere) Lagequaternion.

function qnb = qdelphi(qpb, phi)
    qnb = qmul(rv2q(phi), qpb);

7. Berechnen Sie den Fehlausrichtungswinkelfehler aus der Quaternion und der realen Quaternion: qq2phi

Erstens gemäß der Formel $Q_{N^{\text{'}}}^{}=Q_B^{}\circ \left(Q_B^{N^{}}\right){}^{\ast }$ Ermitteln Sie die Fehlerquaternion$Q_{N^{\text{'}}}^{}$, und dann durch $Q_{N^{\text{'}}}^{}$Auflösen nach dem Fehlausrichtungswinkel $\varphi$ .

function phi = qq2phi(qpb, qnb)
    qnp = qmul(qnb, qconj(qpb));
    phi = q2rv(qnp);

3. Konvertierung verschiedener Gestendarstellungen

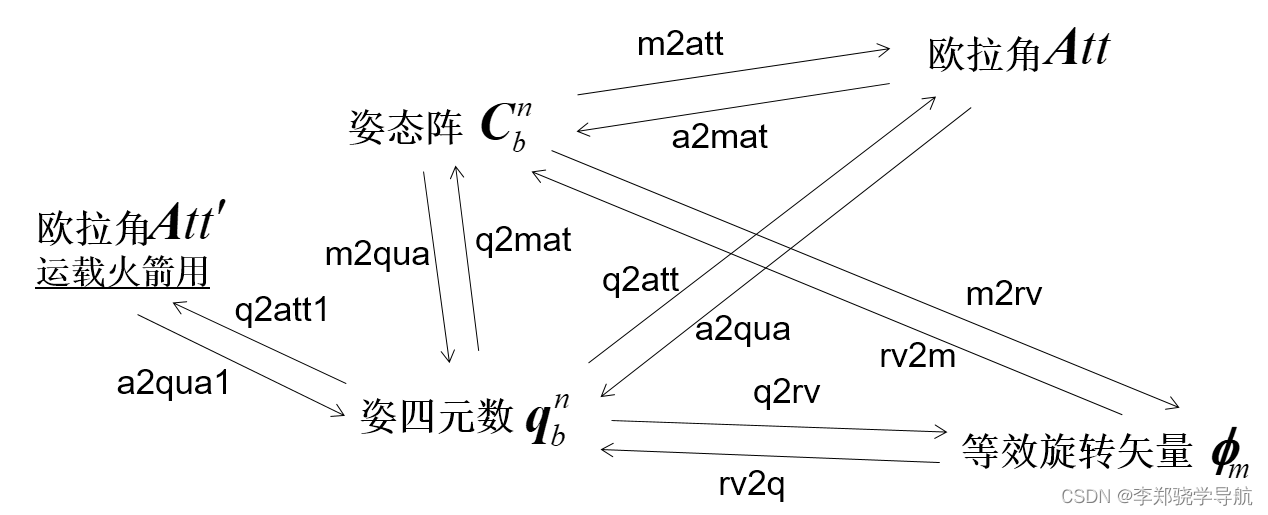
1. Euler-Winkel -> Lagematrix: a2mat

Der Euler-Winkel verwendet drei Auswahlen, um die Lageänderung darzustellen, und die drei Auswahlmatrizen werden multipliziert, um die Richtungskosinusmatrix (Lagematrix) zu erhalten, und die Rotationsreihenfolge ist entscheidend.
$$\begin{array}{l}{C}_B^{}=C_{}{C}_{}{C}_{}=\left[\begin{array}{ccc}{C}_{}& -s_{}& 0\\ S_P& C_{}& 0\\ & & \end{array}\right]\left[\begin{array}{ccc}1& 0& 0\\ 0& C_{}& -s_{}\\ & S_{}& C_{}\end{array}\right]\left[\begin{array}{ccc}{C}_{}& 0& S_{}\\ 0& 1& 0\\ -s_{}& & C_{}\end{array}\right]=\\ \left[\begin{array}{ccc}{C}_{}{C}_{}-S_{}{S}_{}{S}_{}& -s_{}{C}_{}& C_{}{S}_{}+S_{}{S}_{}{C}_{}\\ S_{}{C}_{}+C_{}{S}_{}{S}_{}& C_{}{C}_{}& S_{}{S}_{}-C_{}{S}_{}{C}_{}\\ -c_{}{S}_{}& S_{}& C_{}{C}_{}\end{array}\right]=\left[\begin{array}{ccc}{C}_{}& C_{}& C_{}\\ C_{}& C_{}& C_{}\\ C_{}& C_{}& C_{}\end{array}\right]\end{array}$$

function [Cnb, Cnbr] = a2mat(att)
% Convert Euler angles to direction cosine matrix(DCM).
% 欧拉角->姿态阵
% Prototype: [Cnb, Cnbr] = a2mat(att)
% Input: att - att=[pitch; roll; yaw] in radians
% Outputs: Cnb - DCM from navigation-frame(n) to body-frame(b), in yaw->pitch->roll
%                (3-1-2) rotation sequence
%          Cnbr - DCM in yaw->roll->pitch (3-2-1) rotation sequence
    s = sin(att); c = cos(att);
    si = s(1); sj = s(2); sk = s(3); 
    ci = c(1); cj = c(2); ck = c(3);
    Cnb = [ cj*ck-si*sj*sk, -ci*sk,  sj*ck+si*cj*sk;
            cj*sk+si*sj*ck,  ci*ck,  sj*sk-si*cj*ck;
           -ci*sj,           si,     ci*cj           ];
    if nargout==2  % dual Euler angle DCM
        Cnbr = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;
                 cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;
                -sj,    si*cj,          ci*cj            ];
    endfunction [Cnb, Cnbr] = a2mat(att)
    s = sin(att); c = cos(att);
    si = s(1); sj = s(2); sk = s(3); 
    ci = c(1); cj = c(2); ck = c(3);
    Cnb = [ cj*ck-si*sj*sk, -ci*sk,  sj*ck+si*cj*sk;
            cj*sk+si*sj*ck,  ci*ck,  sj*sk-si*cj*ck;
           -ci*sj,           si,     ci*cj           ];
    if nargout==2  % dual Euler angle DCM
        Cnbr = [ cj*ck, si*sj*ck-ci*sk, ci*sj*ck+si*sk;
                 cj*sk, si*sj*sk+ci*ck, ci*sj*sk-si*ck;
                -sj,    si*cj,          ci*cj            ];
    end

AI-Erklärung :
Dieser Code ist eine Funktion, die Euler-Winkel in eine Posenmatrix umwandelt. Es generiert zwei Ausgabeparameter: Cnb und Cnbr, die jeweils die Lagematrix vom Navigationssystem zum Flugzeugsystem und eine weitere Lagematrix vom Navigationssystem zum Flugzeugsystem darstellen. Wenn die Anzahl der Ausgabeparameter der Funktion 2 beträgt (dh Cnb und Cnbr müssen gleichzeitig generiert werden), wird auch die Cnbr-Matrix berechnet. Die Cnbr-Matrix ist in einer „Gier-Roll-Pitch“-Rotationsreihenfolge (3-2-1) aufgebaut.

2. Attitude-Array -> Euler-Winkel: m2att

$$\begin{array}{l}ich=\mathrm{Arcsin}\left(C_{}\right)\\ \{\begin{array}{l}C=-für\; den\; Zweck2\left(C_{},C_{}\right)\\ P=-für\; den\; Zweck2(C_{},C_{}\end{array}|C_{}|⩽\mathrm{0,999999}\\ \{\begin{array}{ll}C=für\; den\; Zweck2\left(C_{},C_{}\right)& |C_{}|>\mathrm{0,999,999}\\ P=& \end{array}\end{array}$$

function [att, attr] = m2att(Cnb)
% Convert direction cosine matrix(DCM) to Euler attitude angles.
% 姿态阵 -> 欧拉角
% Prototype: [att, attr] = m2att(Cnb)
% Input: Cnb - DCM from navigation-frame(n) to body-frame(b)
% Outputs: att - att=[pitch; roll; yaw] in radians, in yaw->pitch->roll
    att = [ asin(Cnb(3,2));
            atan2(-Cnb(3,1),Cnb(3,3)); 
            atan2(-Cnb(1,2),Cnb(2,2)) ];
    if nargout==2  % dual Euler angles
        attr = [ atan2(Cnb(3,2),Cnb(3,3)); 
                 asin(-Cnb(3,1)); 
                 atan2(Cnb(2,1),Cnb(1,1)) ];
    end

AI-Erklärung :
Dieser Code ist eine MATLAB-Funktion zur Konvertierung der Richtungskosinusmatrix (DCM) in den Euler-Attitude-Winkel. Der Funktionsname ist m2att, der Eingabeparameter ist die DCM-Matrix Cnb, der Ausgabeparameter ist der Euler-Lagewinkel att und die optionale Rotationsachse und der Rotationswinkel attr. Die Funktion des Codes ist wie folgt:

1. Drücken Sie jede Spalte der DCM-Matrix Cnb als Einheitsvektor aus, der den Rotationsvektor vom Navigationskoordinatensystem (n) zum Körperkoordinatensystem (b) darstellt.
2. Verwenden Sie diese Rotationsvektoren, um die Pose des Körperrahmens relativ zum Navigationsrahmen zu berechnen, was zu Euler-Posewinkeln führt.
3. Speichern Sie den berechneten Euler-Lagewinkel im att-Array, angeordnet in der Reihenfolge Gier -> Nick -> Roll, im Bogenmaß.
4. Wenn der Ausgabeparameter attr in Form eines doppelten Euler-Winkels angegeben wird (durch Beurteilung des Werts der Nargout-Variablen), müssen auch die Rotationsachse und der Rotationswinkel berechnet werden.
5. Die Formel zur Berechnung der Rotationsachse lautet: (Cnb(3,2), Cnb(3,3)), was der Vektor ist, der durch die Elemente in der dritten Zeile, der zweiten Spalte und der dritten Spalte der DCM-Matrix gebildet wird.
6. Die Formel zur Berechnung des Drehwinkels lautet: [-asin(-Cnb(3,1)); atan2(Cnb(2,1), Cnb(1,1))], dh zuerst wird der Drehwinkel berechnet die z-Achse (über DCM) Die Vorzeichen der Elemente in Zeile 3, Spalte 1 der Matrix werden umgekehrt) und dann den Drehwinkel um die x'-Achse berechnen (durch die Elemente in Zeile 2, Spalte 1 und Zeile 1). , Spalte 1 der DCM-Matrix).
7. Speichern Sie die berechnete Rotationsachse und den Rotationswinkel im attr-Array im Bogenmaß.
   Es ist zu beachten, dass der Code die Funktionen asin und atan2 in MATLAB verwendet, um die Arkussinus- und Arkuskosinusfunktionen darzustellen und den Wert der Nargout-Variablen zu beurteilen, um die Form des Ausgabeparameters zu bestimmen.

3. Quaternion -> Einstellungsmatrix: q2mat

$$C_B^{}=\left[\begin{array}{ccc}{Q}_0^{}+Q_1^{}-Q_2^{}-Q_3^{}& 2\left(q_{}{Q}_{}-Q_{}{Q}_{}\right)& 2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)\\ 2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)& Q_0^{}-Q_1^{}+Q_2^{}-Q_3^{}& 2\left(q_{}{Q}_{}-Q_{}{Q}_{}\right)\\ 2(q_{}{Q}_{}-Q_{}{Q}_{}& 2(q_{}{Q}_{}+Q_{}{Q}_{}& Q_0^{}-Q_1^{}-Q_2^{}+Q_3^{}\end{array}\right]$$

function Cnb = q2mat(qnb)
% Convert attitude quaternion to direction cosine matrix(DCM).
% 四元数 -> 姿态阵
% Prototype: Cnb = q2mat(qnb)
% Input: qnb - attitude quaternion
% Output: Cnb - DCM from body-frame to navigation-frame
    q11 = qnb(1)*qnb(1); q12 = qnb(1)*qnb(2); q13 = qnb(1)*qnb(3); q14 = qnb(1)*qnb(4); 
    q22 = qnb(2)*qnb(2); q23 = qnb(2)*qnb(3); q24 = qnb(2)*qnb(4);     
    q33 = qnb(3)*qnb(3); q34 = qnb(3)*qnb(4);  
    q44 = qnb(4)*qnb(4);
    Cnb = [ q11+q22-q33-q44,  2*(q23-q14),     2*(q24+q13);
            2*(q23+q14),      q11-q22+q33-q44, 2*(q34-q12);
            2*(q24-q13),      2*(q34+q12),     q11-q22-q33+q44 ];

4. Attitude Array -> Quaternion: m2qua

q 0 2 + q 1 2 − q 2 2 − q 3 2 = C 11 q 0 2 − q 1 2 + q 2 2 − q 3 2 = C 22 q 0 2 − q 1 2 − q 2 2 + q 3 2 = C 33 q 0 2 + q 1 2 + q 2 2 + q 3 2 = 1 } ⇒ ∣ q 0 ∣ = 0,5 1 + C 11 + C 22 + C 33 ∣ q 1 ∣ = 0,5 1 + C 11 − C 22 − C 33 ∣ q 2 ∣ = 0,5 1 − C 11 + C 22 − C 33 ∣ q 3 ∣ = 0,5 1 − C 11 − C 22 + C 33 \left.\begin{array}{l}q_{ 0}^{2}+q_{1}^{2}-q_{2}^{2}-q_{3}^{2}=C_{11} \\ q_{0}^{2}-q_ {1}^{2}+q_{2}^{2}-q_{3}^{2}=C_{22} \\ q_{0}^{2}-q_{1}^{2}- q_{2}^{2}+q_{3}^{2}=C_{33} \\ q_{0}^{2}+q_{1}^{2}+q_{2}^{2} +q_{3}^{2}=1\end{array}\right\} \Rightarrow \begin{array}{l}\left|q_{0}\right|=0,5 \sqrt{1+C_{11 }+C_{22}+C_{33}} \\ \left|q_{1}\right|=0,5 \sqrt{1+C_{11}-C_{22}-C_{33}} \\ \left |q_{2}\right|=0,5 \sqrt{1-C_{11}+C_{22}-C_{33}} \\ \left|q_{3}\right|=0,5 \sqrt{1-C_ {11}-C_{22}+C_{33}}\end{array}Q02+Q12−Q22−Q32=C11Q02−Q12+Q22−Q32=C22Q02−Q12−Q22+Q32=C33Q02+Q12+Q22+Q32=1⎭ ⎬ ⎫⇒∣ q0∣=0,51+C11+C22+C33 ​∣ q1∣=0,51+C11−C22−C33 ​∣ q2∣=0,51−C11+C22−C33 ​∣ q3∣=0,51−C11−C22+C33 ​​

2 ( q 1 q 2 − q 0 q 3 ) = C 12 2 ( q 1 q 2 + q 0 q 3 ) = C 21 2 ( q 1 q 3 + q 0 q 2 ) = C 13 2 ( q 1 q 3 − q 0 q 2 ) = C 31 2 ( q 2 q 3 − q 0 q 1 ) = C 23 2 ( q 2 q 3 + q 0 q 1 ) = C 32 } ⇒ 4 q 0 q 1 = C 32 − C 23 4 q 0 q 2 = C 13 − C 31 4 q 0 q 3 = C 21 − C 12 4 q 1 q 2 = C 12 + C 21 4 q 1 q 3 = C 13 + C 31 4 q 2 q 3 = C 23 + C 32 } \left.\left.\begin{array}{l}2\left(q_{1} q_{2}-q_{0} q_{3}\right)=C_{12} \\ 2\left(q_{1} q_{2 }+q_{0} q_{3}\right)=C_{21} \\ 2\left(q_{1} q_{3}+q_{0} q_{2}\right)=C_{13} \ \ 2\left(q_{1} q_{3}-q_{0} q_{2}\right)=C_{31} \\ 2\left(q_{2} q_{3}-q_{0} q_ {1}\right)=C_{23} \\ 2\left(q_{2} q_{3}+q_{0} q_{1}\right)=C_{32}\end{array}\right\ } \Rightarrow \begin{array}{l}4 q_{0} q_{1}=C_{32}-C_{23} \\ 4 q_{0} q_{2}=C_{13}-C_{31 } \\ 4 q_{0} q_{3}=C_{21}-C_{12} \\ 4 q_{1} q_{2}=C_{12}+C_{21} \\ 4 q_{1} q_{3}=C_{13}+C_{31} \\ 4 q_{2} q_{3}=C_{23}+C_{32}\end{array}\right\}2( q1Q2−Q0Q3)=C122( q1Q2+Q0Q3)=C212( q1Q3+Q0Q2)=C132( q1Q3−Q0Q2)=C312( q2Q3−Q0Q1)=C232( q2Q3+Q0Q1)=C32​⎭ ⎬ ⎫⇒4 q0Q1=C32−C234 q0Q2=C13−C314 q0Q3=C21−C124 q1Q2=C12+C214 q1Q3=C13+C314 q2Q3=C23+C32​⎭ ⎬ ⎫

Schon allein nach Formel eins wird es schwierig sein, die positiven und negativen Vorzeichen jedes Elements der Quaternion zu bestimmen. Wenn ein bestimmtes Element der Quaternion bekannt ist, können andere Elemente gemäß Formel 2 gelöst werden, es muss jedoch vermieden werden, dass das bekannte Element 0 ist. Durch Quaternion-Normalisierungsbedingung $Q_0^{}+Q_1^{}$ $+q_2^{}+Q_3^{}=1$ zeigt, dass es max ⁡ ( qi 2 ) ⩾ 1 / 4 \max \left(q_{i}^{2}\right) \geqslant 1 / 4 gebenmuss$\max \left(q_{ich}^{}\right)⩾1/4$ ist festgelegt, das heißt, es muss ein ∣ qi ∣ ⩾ \left|q_{i}\right| \geqslantunter den vier Elementen$|q_{}|⩾$ $1/2$ . In der praktischen Anwendung kann ein bestimmtes größeres Element$Q_{}$(Es kann als positiver Wert angenommen werden) und dann die verbleibenden drei Elemente gemäß der Formel (B. 10) berechnen.

function qnb = m2qua(Cnb)
% Convert direction cosine matrix(DCM) to attitude quaternion.
%
% Prototype: qnb = m2qua(Cnb)
% Input: Cnb - DCM from body-frame to navigation-frame
% Output: qnb - attitude quaternion
    C11 = Cnb(1,1); C12 = Cnb(1,2); C13 = Cnb(1,3); 
    C21 = Cnb(2,1); C22 = Cnb(2,2); C23 = Cnb(2,3); 
    C31 = Cnb(3,1); C32 = Cnb(3,2); C33 = Cnb(3,3); 
%     q0t = 0.5*sqrt(1+C11+C22+C33);
%     q1t = 0.5*sqrt(1+C11-C22-C33);
%     q2t = 0.5*sqrt(1-C11+C22-C33);
%     q3t = 0.5*sqrt(1-C11-C22+C33);
    if C11>=C22+C33
        q1 = 0.5*sqrt(1+C11-C22-C33);  qq4 = 4*q1;
        q0 = (C32-C23)/qq4; q2 = (C12+C21)/qq4; q3 = (C13+C31)/qq4;
    elseif C22>=C11+C33
        q2 = 0.5*sqrt(1-C11+C22-C33);  qq4 = 4*q2;
        q0 = (C13-C31)/qq4; q1 = (C12+C21)/qq4; q3 = (C23+C32)/qq4;
    elseif C33>=C11+C22
        q3 = 0.5*sqrt(1-C11-C22+C33);  qq4 = 4*q3;
        q0 = (C21-C12)/qq4; q1 = (C13+C31)/qq4; q2 = (C23+C32)/qq4;
    else
        q0 = 0.5*sqrt(1+C11+C22+C33);  qq4 = 4*q0;
        q1 = (C32-C23)/qq4; q2 = (C13-C31)/qq4; q3 = (C21-C12)/qq4;
    end
    qnb = [q0; q1; q2; q3];

AI-Erklärung :
Die Funktion akzeptiert einen Eingabeparameter Cnb, bei dem es sich um eine 3x3-Matrix handelt, die das DCM vom Körperkoordinatensystem zum Navigationskoordinatensystem darstellt. Die Ausgabe der Funktion ist ein Quaternionvektor qnb, der die entsprechende Lage für ein gegebenes DCM darstellt. Die Implementierung des Codes ist wie folgt:

1. Extrahieren Sie Elementwerte aus der Eingabe-Cnb-Matrix und weisen Sie sie den Variablen C11, C12, C13, C21, C22, C23, C31, C32 bzw. C33 zu.
2. Basierend auf den Elementwerten des DCM wird eine Reihe von bedingten Anweisungen verwendet, um zu bestimmen, wie jedes Element berechnet wird, und dann werden die einzelnen Elemente des Quaternionvektors berechnet.
3. Wählen Sie entsprechend dem Ergebnis der bedingten Beurteilung eine geeignete Berechnungsmethode aus, um den endgültigen Quaternionvektor qnb zu erhalten.

5. Euler-Winkel -> Quaternion: a2qua

Quaternionen werden häufig in Algorithmen zur Aktualisierung der Trägheitsnavigationslage verwendet. Die Ausgabeergebnisse der Trägheitsnavigation werden häufig als Euler-Winkel ausgedrückt, und eine gegenseitige Konvertierung zwischen Quaternionen und Euler-Winkeln ist erforderlich. Gemäß der geometrischen Bedeutung von Einheitsquaternionen:
$$\begin{array}{rl}{Q}_B^{}=& Q_{}\circ F_{}\circ Q_{}=\left({ca}_{\psi /}+k{s}_{\psi /}\right)\circ \left({ca}_{\theta /}+ich{bin}_{\theta /}\right)\circ \left({ca}_{c/}+j{s}_{c/}\right)=\\ & \left({ca}_{\psi /}{C}_{\theta /}+ich{c}_{\psi /}{S}_{\theta /}+k{s}_{\psi /}{C}_{\theta /}+k\circ {ich}_{\psi /}{S}_{\theta /}\right)\circ \left({ca}_{c/}+j{s}_{c/}\right)=\\ & \left({ca}_{\psi /}{C}_{\theta /}+ich{c}_{\psi /}{S}_{\theta /}+k{s}_{\psi /}{C}_{\theta /}+j{s}_{\psi /}{S}_{\theta /}\right)\circ \left({ca}_{c/}+j{s}_{c/}\right)=\\ & \left[\begin{array}{l}{C}_{\psi /}{C}_{\theta /}{C}_{c/}-S_{\psi /}{S}_{\theta /}{S}_{c/}\\ C_{\psi /}{S}_{\theta /}{C}_{c/}-S_{\psi /}{C}_{\theta /}{S}_{c/}\\ S_{\psi /}{S}_{\theta /}{C}_{c/}+C_{\psi /}{C}_{\theta /}{S}_{c/}\\ S_{\psi /}{C}_{\theta /}{C}_{c/}+C_{\psi /}{S}_{\theta /}{S}_{c/}\end{array}\right]\end{array}$$

function qnb = a2qua(att)
% Convert Euler angles to attitude quaternion.
% 欧拉角 -> 四元数
% Prototype: qnb = a2qua(att)
% Input: att - att=[pitch; roll; yaw] in radians
% Output: qnb - attitude quaternion
    att2 = att/2;
    s = sin(att2); c = cos(att2);
    sp = s(1); sr = s(2); sy = s(3); 
    cp = c(1); cr = c(2); cy = c(3); 
    qnb = [ cp*cr*cy - sp*sr*sy;
            sp*cr*cy - cp*sr*sy;
            cp*sr*cy + sp*cr*sy;
            cp*cr*sy + sp*sr*cy ];

AI-Erklärung :
Die Ausgabe der Zahl ist ein Quaternion qnb, das die Haltung darstellt, die dem gegebenen Euler-Winkel entspricht. Die Implementierung des Codes ist wie folgt:

1. Teilen Sie den att-Vektor durch 2, um den att2-Vektor zu erhalten, der die Hälfte jedes Winkels darstellt.
2. Verwenden Sie die Funktionen sin und cos, um die Sinus- und Cosinuswerte des att2-Vektors zu berechnen und die entsprechenden s- und c-Vektoren zu erhalten.
3. Weisen Sie die Elemente der s- und c-Vektoren für nachfolgende Berechnungen den Variablen sp, sr, sy, cp, cr und cy zu.
4. Berechnen Sie jedes Element der Quaternion qnb gemäß der Formel der Quaternion.

6. Quaternion -> Euler-Winkel: q2att

Es ist nicht einfach, den Euler-Winkel direkt durch Quaternion zu lösen, und die Haltungsmatrix kann als Zwischenübergangsbetrag verwendet werden.
$$\begin{array}{l}ich=\mathrm{Arcsin}\left(2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)\right)\\ \left\{\begin{array}{ll}C=-für\; den\; Zweck2\left(2\left(q_{}{Q}_{}-Q_{}{Q}_{}\right),Q_0^{}-Q_1^{}-Q_2^{}+Q_3^{}\right)& \\ P=-für\; den\; Zweck2(2\left(q_{}{Q}_{}-Q_{}{Q}_{}\right),Q_0^{}-Q_1^{}+Q_2^{}-Q_3^{}& |2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)|⩽\end{array}\right\}\\ \{\begin{array}{ll}C=für\; den\; Zweck2\left(2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right),Q_0^{}+Q_1^{}-Q_2^{}-Q_3^{}\right)& |2\left(q_{}{Q}_{}+Q_{}{Q}_{}\right)|>\mathrm{0,999999}\\ P=& \end{array}\end{array}$$

function att = q2att(qnb)
% Convert attitude quaternion to Euler attitude angles.
% 四元数 -> 欧拉角
% Prototype: att = q2att(qnb)
% Input: qnb - attitude quaternion
% Output: att - Euler angles att=[pitch; roll; yaw] in radians
    q11 = qnb(1)*qnb(1); q12 = qnb(1)*qnb(2); q13 = qnb(1)*qnb(3); q14 = qnb(1)*qnb(4); 
    q22 = qnb(2)*qnb(2); q23 = qnb(2)*qnb(3); q24 = qnb(2)*qnb(4);     
    q33 = qnb(3)*qnb(3); q34 = qnb(3)*qnb(4);  
    q44 = qnb(4)*qnb(4);
    C12=2*(q23-q14);
    C22=q11-q22+q33-q44;
    C31=2*(q24-q13); C32=2*(q34+q12); C33=q11-q22-q33+q44;
    att = [ asin(C32); 
            atan2(-C31,C33); 
            atan2(-C12,C22) ];

AI-Erklärung :
Dieser Code ist eine Funktion, die Quaternionen in Euler-Winkel umwandelt. Es verwendet eine Quaternion als Eingabe und gibt einen Vektor zurück, der die Euler-Winkel (Nick-, Gier- und Rollwinkel) enthält. Die Hauptschritte des Codes sind wie folgt:

1. Variablen definieren: Zunächst zerlegt der Code die Eingabequaternion in die Quadrate ihrer Komponenten und speichert sie in den Variablen q11, q22, q33 und q44. Diese Variablen werden in nachfolgenden Berechnungen verwendet.
2. Definieren der Elemente der Rotationsmatrix: Als Nächstes verwendet der Code die Komponenten der Quaternion, um die Elemente C12, C22, C31, C32 und C33 der Rotationsmatrix zu berechnen. Diese Elemente werden zur Berechnung der Euler-Winkel verwendet.
3. Berechnen Sie Euler-Winkel: Schließlich verwendet der Code die Elemente der Rotationsmatrix, um Euler-Winkel zu berechnen. Verwenden Sie zunächst die Funktion asin, um den Wert von C32 zu berechnen und den Nickwinkel zu erhalten. Verwenden Sie dann die Funktion atan2, um den Tangens der Werte von C31 und C33 zu berechnen und so den Gierwinkel zu erhalten. Verwenden Sie abschließend die Funktion atan2, um den Tangens der Werte von C12 und C22 zu berechnen und so den Rollwinkel zu erhalten.
4. Schließlich gibt die Funktion einen Vektor att zurück, der die Euler-Winkel (Nick-, Gier- und Rollwinkel) enthält. Diese Euler-Winkel stellen den Rotationswinkel der Pose dar, die dem Quaternion im dreidimensionalen Raum entspricht.

7. Quaternion -> Äquivalenter Rotationsvektor: q2rv

function rv = q2rv(q) 
% Convert transformation quaternion to rotation vector.
%  四元数 -> 等效旋转矢量
% Prototype: rv = q2rv(q) 
% Input: q - transformation quaternion
% Output: rv - corresponding rotation vector, such that
	if(q(1)<0)
	    q = -q;
	end
    n2 = acos(q(1));
    if n2>1e-40
        k = 2*n2/sin(n2);
    else
        k = 2;
    end
    rv = k*q(2:4);   % q = [ cos(|rv|/2); sin(|rv|/2)/|rv|*rv ];

AI-Erklärung :
Dieser Code ist eine Funktion, die eine Transformationsquaternion in einen äquivalenten Rotationsvektor umwandelt. Es verwendet eine Quaternion als Eingabe und gibt den entsprechenden Rotationsvektor zurück. Die Hauptschritte des Codes sind wie folgt:

1. Konvertieren des Vorzeichens der Quaternion: Der Code prüft zunächst, ob das erste Element in der Quaternion negativ ist. Wenn es negativ ist, wird die Quaternion negiert, um sicherzustellen, dass das Vorzeichen des Rotationsvektors wie erwartet ist.
2. Berechnen Sie die Größe des Rotationsvektors: Der Code verwendet die Acos-Funktion, um den Arkuskosinus des ersten Elements der Quaternion zu berechnen und die Größe des Rotationsvektors (auch als Rotationswinkel bezeichnet) zu erhalten. Hier wird eine bedingte Anweisung verwendet: Wenn n2 (d. h. der Drehwinkel) größer als ein kleiner Schwellenwert (1e-40) ist, wird die Größe des Rotationsvektors durch eine Formel berechnet; andernfalls beträgt die Größe des Rotationsvektors auf 2 gesetzt.
3. Berechnen Sie die Richtung des Rotationsvektors: Entsprechend der Größe des Rotationsvektors berechnet der Code mithilfe der Sinus- und Cos-Funktionen die Richtung des Rotationsvektors, der dem zweiten bis vierten Element der Quaternion entspricht. Konkret wird die Richtung des Rotationsvektors durch Multiplikation der Größe des Rotationsvektors mit dem Produkt des zweiten bis vierten Elements der Quaternion ermittelt.
4. Schließlich gibt die Funktion den berechneten Rotationsvektor rv zurück. Dieser Rotationsvektor stellt den äquivalenten Rotationsvektor der Haltung dar, die dem Quaternion im dreidimensionalen Raum entspricht.

Beachten Sie, dass während der Konvertierung das Codezeichen das Eingabequaternion anpasst, um sicherzustellen, dass das Vorzeichen des Rotationsvektors wie erwartet ist.

8. Äquivalenter Rotationsvektor -> Quaternion: rv2q

Konvertieren Sie zunächst die Quaternion in eine skalare nichtnegative Quaternion und zweitens gemäß der Formel $Q=Q_{}+Q_{}=\cos \frac{}{2}+u\mathrm{Sünde}\frac{}{2}=$ $\cos \frac{}{2}+\frac{}{2}\cdot \frac{sin(\varphi /2}{\varphi /2}$, zunächst aus der skalaren Beziehung der Quaternion $Q_{}=\cos \frac{}{2}$Finden Sie die Hälfte des Moduls des Rotationsvektors $\frac{}{2}=$ $\arccos \left(q_{}\right)$ , und dann durch die Vektorrelation$Q_{}=\frac{}{2}\cdot \frac{sin(\varphi /2}{\varphi /2}$Finden Sie den äquivalenten Rotationsvektor $\varphi =2\frac{(\varphi /2}{sin(\varphi /2)}{Q}_{}$Q = q 0 + qv = cos ⁡ ϕ 2 + u sin ⁡ ϕ 2 Q=q_{0} +
$$Q=Q_{}+Q_{}=\cos \frac{}{2}+u\mathrm{Sünde}\frac{}{2}$$

function q = rv2q(rv)
% Convert rotation vector to transformation quaternion.
%
% Prototype: q = rv2q(rv)
% Input: rv - rotation vector
% Output: q - corresponding transformation quaternion, such that
%             q = [ cos(|rv|/2); sin(|rv|/2)/|rv|*rv ]
    q = zeros(4,1);
    n2 = rv(1)*rv(1) + rv(2)*rv(2) + rv(3)*rv(3);
    if n2<1.0e-8  % cos(n/2)=1-n2/8+n4/384; sin(n/2)/n=1/2-n2/48+n4/3840
        q(1) = 1-n2*(1/8-n2/384); s = 1/2-n2*(1/48-n2/3840);
    else
        n = sqrt(n2); n_2 = n/2;
        q(1) = cos(n_2); s = sin(n_2)/n;
    end
    q(2) = s*rv(1); q(3) = s*rv(2); q(4) = s*rv(3);

Dieser Code ist eine Funktion, die einen Rotationsvektor in eine Transformationsquaternion umwandelt. Es verwendet einen Rotationsvektor als Eingabe und gibt die entsprechende Transformationsquaternion zurück. Die Hauptschritte des Codes sind wie folgt:

1. Initialisieren Sie die Quaternion: Der Code erstellt zunächst einen Nullvektor q der Größe 4, der zum Speichern der Elemente der transformierten Quaternion verwendet wird.
2. Berechnen Sie die Größe des Rotationsvektors: Der Code verwendet das erste Element des Rotationsvektors als Größe des Rotationsvektors (auch als Rotationswinkel bezeichnet). Hier wird eine bedingte Anweisung verwendet. Wenn das Normquadrat des Rotationsvektors kleiner als ein kleiner Schwellenwert (1,0e-8) ist, wird die Größe des Rotationsvektors mithilfe der Taylor-Reihenentwicklung berechnet; andernfalls beträgt die Größe des Rotationsvektors nach der Standardformel berechnet.
3. Berechnen Sie die Richtung des Rotationsvektors: Basierend auf der Größe des Rotationsvektors verwendet der Code die Sin- und Cos-Funktionen, um die Richtung des Rotationsvektors zu berechnen. Konkret wird die Richtung des Rotationsvektors durch Multiplikation der Größe des Rotationsvektors mit dem Vorzeichen des ersten Elements des Rotationsvektors und Multiplikation des Ergebnisses mit den anderen drei Elementen des Rotationsvektors erhalten.
4. Transformationsquaternion konstruieren: Entsprechend der Größe und Richtung des Rotationsvektors erstellt der Code die entsprechende Transformationsquaternion. Teilen Sie insbesondere die Größe des Rotationsvektors durch 2 und verwenden Sie dann die Sinus- und Cosinus-Funktionen, um die einzelnen Elemente der Transformationsquaternion zu berechnen.
5. Schließlich gibt die Funktion die berechnete Transformationsquaternion q zurück. Diese Transformationsquaternion stellt die Darstellung der Pose dar, die dem Rotationsvektor im Quaternionraum entspricht.

Beachten Sie, dass der Code im Berechnungsprozess unterschiedliche Formeln verwendet, um mit unterschiedlichen Situationen der Größe des Rotationsvektors umzugehen und die Berechnungsgenauigkeit zu verbessern.

9. Attitude Array -> Äquivalenter Rotationsvektor: m2rv

function rv = m2rv(m)
% Convert transformation matrix to rotation vector.
%
% Prototype: rv = m2rv(m)
% Input: m - transformation matrix
% Output: rv - corresponding rotation vector, such that
        rv = [m(3,2)-m(2,3); m(1,3)-m(3,1); m(2,1)-m(1,2)];  % 11/10/2022
        phi = acos((m(1,1)+m(2,2)+m(3,3)-1)/2);
        if phi<1e-10, afa=1/2; else afa=phi/(2*sin(phi)); end
%         afa = phi/sqrt(rv'*rv);
        rv = afa*rv;
        return;
%     rv = iaskew(m-glv.I33);  % coarse init is ok when rv is small, otherwise may fail
%     rvx = askew(rv); % good! the following iteration due to the
    for k=1:2        % accuracy deduce of sqrt(.) in function m2qua
        xx = rv(1)*rv(1); xy = rv(1)*rv(2); xz = rv(1)*rv(3);
        yy = rv(2)*rv(2); yz = rv(2)*rv(3); zz = rv(3)*rv(3);
        n2 = xx+yy+zz;
%         n2 = rv'*rv; 
        if n2>1.0e-40
            n = sqrt(n2);
%             rvx = (m-eye(3)-(1-cos(n))/n2*rvx*rvx) * (n/sin(n));
            rvx = (m1-(1-cos(n))/n2*[-yy-zz,xy,xz; xy,-xx-zz,yz; xz,yz,-xx-yy]) * (n/sin(n));
            rv = [rvx(3,2); rvx(1,3); rvx(2,1)]; % rv = iaskew(rvx);
        else
            rv = zeros(3,1);
            break;
        end
    end

AI-Erklärung:
Dieser Code ist eine Funktion, die eine Transformationsmatrix in einen Rotationsvektor umwandelt. Seine Hauptfunktionen sind wie folgt:

1. Berechnen Sie den Rotationsvektor: Durch Subtrahieren der Elemente auf der Diagonale von den Elementen der Transformationsmatrix und anschließendes Anwenden eines bestimmten Berechnungsschritts wird der Rotationsvektor erhalten.
2. Berechnen Sie den Drehwinkel: Verwenden Sie die Funktion acos, um den Drehwinkel im Rotationsvektor zu berechnen.
3. Berechnen Sie den Normalisierungskoeffizienten des Rotationsvektors: Berechnen Sie den Normalisierungskoeffizienten des Rotationsvektors entsprechend dem Wert des Rotationswinkels. Wenn der Drehwinkel sehr klein ist (weniger als 1e-10), stellen Sie den Normalisierungsfaktor auf 1/2 ein, andernfalls berechnen Sie gemäß der Formel.
4. Rotationsvektor normalisieren: Normalisiert den Rotationsvektor mithilfe eines Normalisierungsfaktors.
5. Berechnen Sie den Rotationsvektor iterativ: Berechnen Sie den Rotationsvektor iterativ durch eine Schleife. Initialisieren Sie zunächst den Rotationsvektor auf einen Vektor mit einem kleinen Unterschied zur Transformationsmatrix (mithilfe von Grobinitialisierung). Anschließend wird der Rotationsvektor durch eine Reihe von Rechenschritten aktualisiert. Dieser iterative Prozess wird zweimal durchgeführt.

10. Äquivalenter Rotationsvektor -> Lagematrix: rv2m

$$C_B^{}=ICH+\frac{\mathrm{Sünde}}{\varphi }(\varphi \times )+\frac{1-\cos }{{\varphi }^2}(\varphi \times {)}^2$$

function m = rv2m(rv)
% Convert rotation vector to transformation matrix.
% 等效旋转矢量 -> 姿态阵
% Prototype: m = rv2m(rv)
% Input: rv - rotation vector
% Output: m - corresponding DCM, such that

	xx = rv(1)*rv(1); yy = rv(2)*rv(2); zz = rv(3)*rv(3);
	n2 = xx+yy+zz;
    if n2<1.e-8
        a = 1-n2*(1/6-n2/120); b = 0.5-n2*(1/24-n2/720);  % a->1, b->0.5
    else
        n = sqrt(n2);
        a = sin(n)/n;  b = (1-cos(n))/n2;
    end
	arvx = a*rv(1);  arvy = a*rv(2);  arvz = a*rv(3);
	bxx = b*xx;  bxy = b*rv(1)*rv(2);  bxz = b*rv(1)*rv(3);
	byy = b*yy;  byz = b*rv(2)*rv(3);  bzz = b*zz;
	m = zeros(3,3);
	% m = I + a*(rvx) + b*(rvx)^2;
	m(1)=1     -byy-bzz; m(4)= -arvz+bxy;     m(7)=  arvy+bxz;
	m(2)=  arvz+bxy;     m(5)=1     -bxx-bzz; m(8)= -arvx+byz;
	m(3)= -arvy+bxz;     m(6)=  arvx+byz;     m(9)=1     -bxx-byy;

AI-Erklärung:
Diese Funktion ist eine Funktion, die einen Rotationsvektor in eine Posenmatrix umwandelt. Es verwendet einen Rotationsvektor als Eingabe und gibt die entsprechende Posenmatrix als Ausgabe zurück. Der Prozess ist wie folgt:

1. Zunächst berechnet die Funktion die drei Komponenten des Rotationsvektors (dh xx, yy und zz), indem sie das Skalarprodukt des Eingaberotationsvektors bzw. des Einheitsvektors bildet.
2. Als nächstes berechnet die Funktion eine Variable n2, die gleich der Summe der Quadrate der drei Komponenten des Rotationsvektors ist. Wenn n2 kleiner als ein kleiner Schwellenwert (1.e-8) ist, liegt die Länge des Rotationsvektors sehr nahe bei Null. In diesem Fall wird eine Näherungslösung zur Berechnung der Elemente der Posenmatrix verwendet.
3. Wenn n2 größer oder gleich 1.e-8 ist, bedeutet dies, dass die Länge des Rotationsvektors nicht Null ist. Zu diesem Zeitpunkt wird die Taylor-Reihenerweiterung verwendet, um die Elemente der Lagematrix zu berechnen. In diesem Fall berechnet die Funktion zunächst die Länge n des Rotationsvektors und berechnet dann die Werte von sin(n) und (1-cos(n)) entsprechend der Länge n, die zum Konstruieren verwendet werden Elemente der Posenmatrix.
4. Als nächstes konstruiert die Funktion jedes Element der Posenmatrix basierend auf den oben berechneten Werten. Zu diesen Elementen gehören a rv(1), a rv(2) und a rv(3) sowie b xx, b rv(1) rv(2), b rv(1) rv(3), by yy, b rv (2) rv(3) und bzz .
5. Abschließend füllt die Funktion diese Elemente in eine 3x3-Matrix und gibt diese Matrix als Ausgabe zurück.

Zusammenfassend besteht die Funktion dieser Funktion darin, den Rotationsvektor in eine Posenmatrix umzuwandeln. Es verwendet Taylor-Reihenentwicklung und Näherungslösungen, um den Fall zu behandeln, in dem die Länge des Rotationsvektors nahe Null liegt, um numerische Instabilitäten zu vermeiden.

11. Antisymmetrisches Array

askew: Finden Sie die antisymmetrische Matrix des dreidimensionalen Vektors

function m = askew(v)
    m = [ 0,     -v(3),   v(2); 
          v(3),   0,     -v(1); 
         -v(2),   v(1),   0     ];