Logestic回归算法笔记
前言
对于分类问题,比如二分类,输出y一共分为负类(记为0)和正类(记为1),即 y∈{0,1}。
如果使用线性回归的方式解决,如果存在与同类样本中特征差别较大的个体,可能导致的得到的假设函数
(θ为待优化参数) 的分类效果较差。
Logestic 函数的引入
符号引入:
m为训练样本个数
n为特征变量个数
θ=
,
…
(T表示转置 )
上标i表示第i个样本
以二分类为例,由于线性回归产生的输出
=
是连续值,而二分类的输出是离散值 (0,1),因此需要引入一个函数来将
压缩在 0 ~ 1 之间。于是便找到了Logestic 函数(又称Sigmoid 函数),如下。
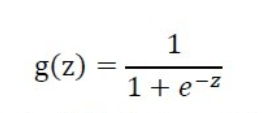
该函数图像如下:
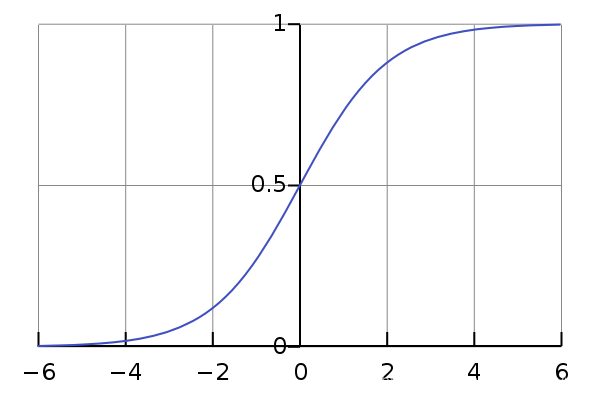
假设函数的引入
那么,新的假设函数
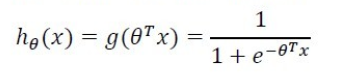
自然地,我们可以作出假设:对每一个输入x,可将
计算得到的值作为 y = 1 此种情况的概率估计,则 y = 0 概率为
。
即:
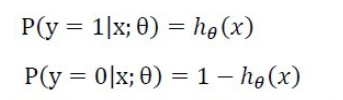
对上面二式进行整理,得
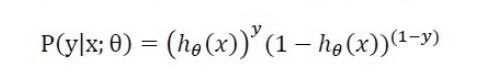
当y=1时,后面一块的值为1,整体计算的是x属于1类的概率。当y=0时,前面一块的值为1,整体计算的则是x属于0类的概率,即
。
极大似然法引入代价函数
若要求取参数θ,我们自然会联想到用线性回归中的平均误差平方和作为代价函数,即
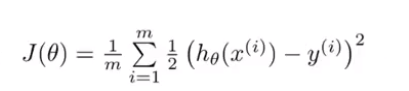
或者直接让代价函数为误差平方和(因为关心的重点是参数θ,1/m只是一个常量,存在与否只是影响
取的是平均误差还是总体误差),即
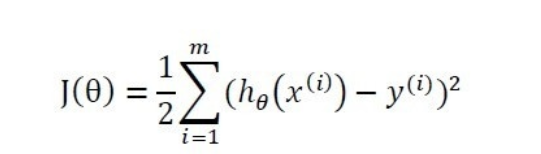
其中,x与y的上标i指的是第i个训练样本。
但是,如果将新的假设函数代入
,由于新的假设函数
中含有Logestic函数这种非线性函数,
得到的
很有可能是非凸函数,这将导致使用梯度下降来最小化
求参数θ时容易出现局部最优从而不利于问题求解。
下面采用极大似然法来获取代价函数。
由于已经知道样本中每组(x,y)出现的概率,即
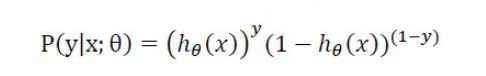
又由于这m个样本独立,那么这m个样本出现的似然函数则为这m个样本各自出现的概率的乘积,即
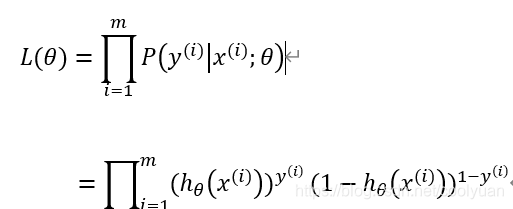
取对数,则
为
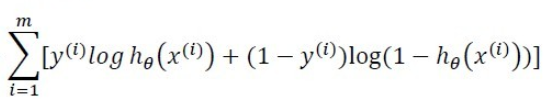
因为极大似然法的目的在于利用已知的样本结果,反推最有可能(最大概率)导致这样样本结果的参数值。
在此例子中是要确定参数
, 使得上式值最大 (即最拟合样本)。
而若要使用梯度下降法使代价函数最小来求解
,就可以令
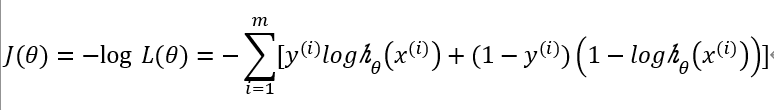
梯度下降法最小化代价函数求θ
使用梯度下降法求解θ,即不断使用
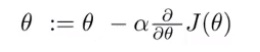
直至
收敛。
在一个样本中,偏导项的计算如下:


表示的是一个样本中的第j个特征量,
表示一个样本中的第j个参数。
那么对于整体样本,θ的更新规则为:
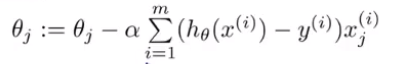
线性回归中使用梯度下降的此更新规则也是如此。其实,对不同的假设函数而言,使用梯度下降法的更新规则都是上式。
结束语
以上便是本人对Logestic回归算法内容的总结,若有错误,还望指正 ~ m( _ _ )m。
