文章目录
6.1 引言
- 现实中存大量聚类问题
- 聚类分析目的
- 把对象按一定规则分成若干类,类不事先给定,
- 而是根据数据特征确定,对类的数目和类的结构不作任何假定。
- 同类里的对象相似,不同类里的对象不相似。
- 聚类分析常探索寻找“自然的”或“实在的”分类,
- 这样的分类应是对所研究的问题有意义的。
- 聚类分析也能够用来概括数据。
- 判别分类和聚类分析
- 都是研究事物分类(或组)的基本法
- 区别:
- 组数目已知,将样品分配给事先已定义好的组(或类)之一;
- 类数目还是类本身在事先都是未知。
- 联系:如果组不是已有,则对组的事先了解和形成有时可通过聚类分析探索;
- 聚类分析的效果往往也可以通过由前两个(或三个)费希尔判别函数得分产生的散点图(或旋转图)从直觉上评估。
- 根据分类对象不同
- Q:对样品的聚类,
- R:对变量的聚类。
- 本章主Q
6.2距离和相似系数
- 对样品(变量)分类,样品(或变量)相似性咋度量?
- 两相似性度量:距离和相似系数
- 距离是不相似性的度量。
- 距离和相似系数有不同的定义,
- 这些定义与变量类型有关
- 间隔变量:变量用连续量表示,如长度
- 有序变量:变量度量时不用明确的数量表示,用等级表示,
- 如某产品分一等、二等、三等
- 名义变量:变量用一些类表示,
- 类之间无等级也无数量关系,
- 性别、职业、产品号
- 间隔变量也称定量变量,
- 有序和名义
- 统定性变量
- 属性变量
- 分类变量
- 对间隔变量,
- 距离度量样品之间相似性,
- 相似系数常度量变量间相似性
- 相似系数也
- 度量基于有序或名义变量的样品间相似性。
- 本章基于间隔变量的样品聚类分析方法
一 距离
- 聚类过程中,相距较近的样品点归一类,
- 较远的样品点应属不同类。
- 常用的距离有如下几:
扫描二维码关注公众号,回复:
8539463 查看本文章


- Minkowski距离
- 。
- 时,
- 绝对值距离,形象称“城市街区”距离
- 当城市街区中位置点之间的远近用路程来度量时
- 用绝对值距离( )比较合适
-
欧氏距离,聚类分析中最常用的距离
-
,
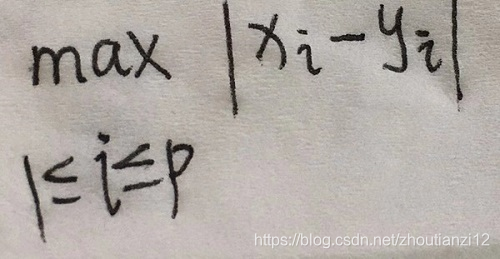
- 切比雪夫距离
- 欧氏距离对(大的)异常值敏感,
- 绝对值距离却对异常值相对不太敏感。
-
越大,差值大的变量在距离计算中起的作用就大,
- 对异常值越敏感。
- 各变量的单位不同或变异性相差很大时
- 不直接用明氏,先对各变量的数据作标准化处理,
- 用标准化后的数据计算距离。
- 最常用的标准化处理是,令
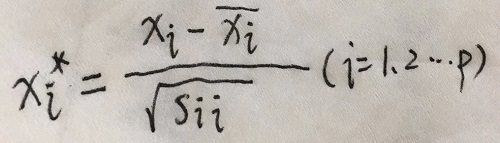
- 的样本均值和样本方差。
- 兰氏距离
- 当数据皆为正,兰氏距离
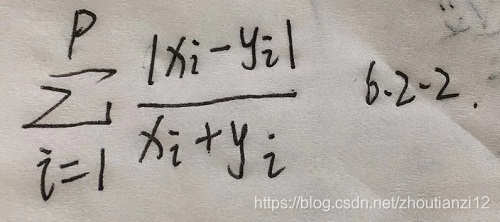
- 距离与各变量单位无关,
- 适用于高度偏斜或含异常值的数据
- 3.马氏距离
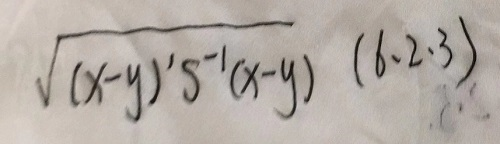
- 样本协方差矩阵。
- 考虑各变量间相关性,与各变量单位无关
- 缺陷,聚类过程中的类一直变化,使类内的样本协方差矩阵(或联合协方差矩阵)难确定,除非有关于不同类的先验知识。
- 实际聚类分析中,马氏不是理想的
- 以上几种要求变量是间隔尺度,
- 如果变量是有序尺度或名义尺度
- 则有相应的一些定义样品之间距离和相似系数的方法。
- 下例给出对二值名义变量的一种简单距离定义
-
例6.2.1
-
学员的资料中得到这样六个变量
-
:性别(男,女)
-
:外语语种(英语,非英语)
-
:专业(统计,非统计)
-
:职业(教师,非教师)
-
:居住处(校内,校外)
-
:学位(硕士,学士)
-
两名:
-
=(男,英语,统计,非教师,校外,学士)
-
=(女,英语,非统计,教师,校外,硕士)
-
记配合的变量数为 ,不配合
- 则距离定义为
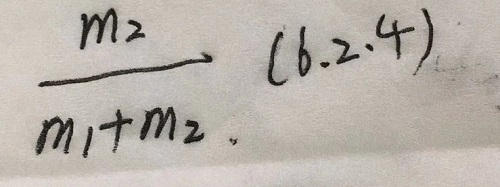
- 本例距离为2/3
二 相似系数
- 对变量聚类时,常用相似系数作为变量间相似性度量。
- 要看大小,另一些看相似系数绝对值大小
- 相似系数(其绝对值)越大,变量间相似性程度越高
- 聚类时,较相似的变量归一类,
- 不太相似的变量属不同类。
- 变量
与
的相似系数用
- 一般满足:

- 常用的相似系数有如下
- 夹角余弦
- 是 中
- 变量 的观测向量与
- 变量 的观测向量间的夹角
- 定义俩变量相似系数为
- 记作
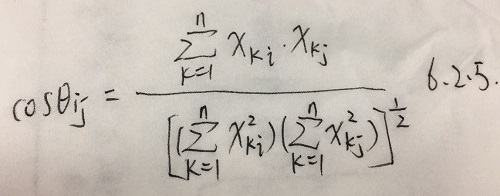
- 相关系数
- 变量与变量的相似系数
- 为样本相关系数 ,记作

- 如果变量
与
皆已标准化了
- 则它们间的夹角余弦就是相关系数
- 相似系数除有时也度量样品间的相似性
- 距离有时也度量变量间相似性
- 由距离来构造相似系数总是可能的,令
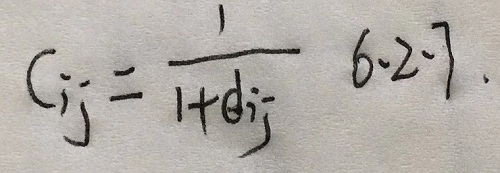
- d为第 个样品与第 的距离,
- 可作为相似系数,来度量样品间相似性
- 然而距离须满足三条件,不总能由相似系数构造。
- 高尔( Gower)证明
- 当相似系数矩阵 非负定时,如令
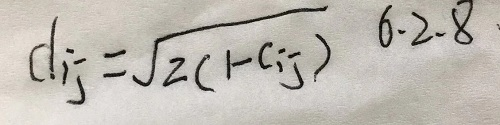
- 则 满足三条件
- 同一批数据用不同的相似性度量,得到不同分类结果
- 聚类分析中,应根据实际情况选取合适的相似性度量。
- 经济变量分析中,常用相关系数来描述变量间的相似性程度。
