Abstract
• 问题:对于嵌入在高维空间的低维流形数据的表示;
• 利用图Laplacian算子、流形上的 Laplacian Beltrami 算子和热方程的对应关系;
• 局部保留能力和与聚类的自然联系。
1 Introduction
• 传统降维方法如PCA、MDS,非线性映射方法如自组织映射和其它基于神经网络的方法,没有有效的方法找到全局最优,没有考虑数据可能存在的流形结构;
• 算法生成的映射可以看作是对流形几何结构连续映射的离散近似;
• 框架:
1)用 adjacency graph 估计 manifold,用 weighted Laplacian 估计 Laplacian Beltrami 算子;
2)LE的局部保留能力使之对于离群点和噪声不敏感,由于只用到局部距离所以也不容易短路。算法隐含地强调了数据的聚类结构,这一点与谱聚类相近;
3)由于算法是基于流形的内在几何结构,所以它在embedding上保持稳定性。
2 The Algorithm
• step 1 ( adjacency graph ):
(a) ε 近邻:几何直观、自然对称,但容易导致图的不连通;
(b) k 近邻:可以连通,但几何不直观;
• step 2 ( weights ):
(a) 热核 (b)无参
• step 3 ( eigenmaps ):
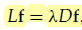
3 Justification
3.1 Optimal Embeddings
• Wij 作为惩罚项,![]() 去除任意缩放,
去除任意缩放,![]() 去除平移
去除平移
一维情况:![]()
多维情况:![]()
3.2 The Laplacian Beltrami Operator
3.3 Heat Kernels and the Choice of Weight Matrix
• 流形Laplacian的几种可能近似方案:
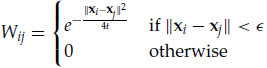
4 Connections to Spectral Clustering
• Normalized cut:
![]()
![]()
这个组合优化问题是NP-hard,但是如果我们允许将指标函数放宽到实值,就可转化为最小化图Laplacian:
![]()
5 Analysis of Locally Linear Embedding Algorithm
( 关于LE和LLE的区别这个问题,我在保研面试的时候也被问到过 )
• step 1( adjacency information ):(a) ε-ball (b)k近邻
• step 2( approximation matrix ):
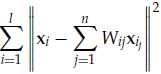
• step 3( embedding ):
![]()
E 与 L 存在如下关系:
![]()
6 Examples
实验,略
7 Conclusions
未解决的问题:
1)不是等距映射。模式识别和数据表示中到底什么样的映射是好的?
2)能估计出流形本征维数的其他几何不变量;
3)隐式地假设了流形上的均匀概率分布;不能清除流形有边界时算法的表现;参数选择问题;需要对嵌入映射的有限样本估计的收敛性进行处理。