版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
前言
读了一下sklearn官方提供的决策树示例,不仅学到了决策树的使用还学到了一些numpy的技巧。
一元回归
# Import the necessary modules and libraries
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
# 计算y并将y扁平化
y = np.sin(X).ravel()
# 修改0、5、10……这些点为噪声点
y[::5] += 3 * (0.5 - rng.rand(16))
# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)
# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black",
c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",
label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
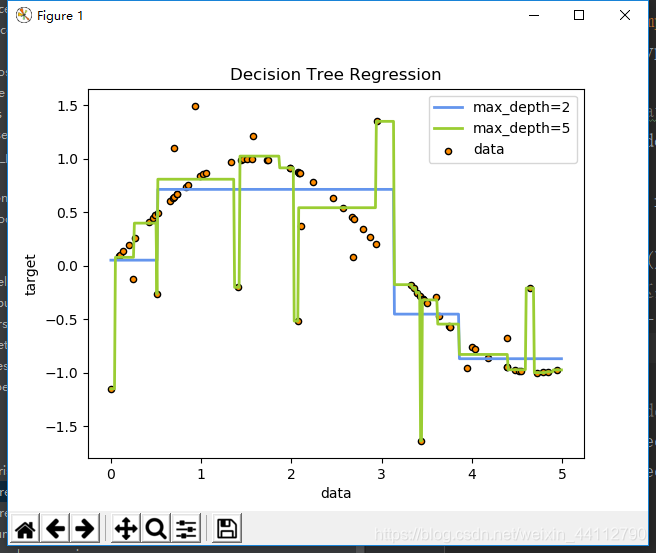
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
可见max_depth=2对于sin(x)曲线来说有些欠拟合,而max_depth=5却过拟合把一些噪声点也拟合了进去。
多输出回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
# 随机数种子相同保证不同人随机的结果相同
rng = np.random.RandomState(1)
# 生成-100到100内的随机数
X = np.sort(200 * rng.rand(100, 1) - 100, axis=0)
# 原点为圆心,半径为PI的圆
y = np.array([np.pi * np.sin(X).ravel(), np.pi * np.cos(X).ravel()]).T
# 每隔五行修改数据为噪声
y[::5, :] += (0.5 - rng.rand(20, 2))
# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_3 = DecisionTreeRegressor(max_depth=8)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)
# Predict
X_test = np.arange(-100.0, 100.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)
# Plot the results
plt.figure()
s = 25
plt.scatter(y[:, 0], y[:, 1], c="navy", s=s,
edgecolor="black", label="data")
plt.scatter(y_1[:, 0], y_1[:, 1], c="cornflowerblue", s=s,
edgecolor="black", label="max_depth=2")
plt.scatter(y_2[:, 0], y_2[:, 1], c="red", s=s,
edgecolor="black", label="max_depth=5")
plt.scatter(y_3[:, 0], y_3[:, 1], c="orange", s=s,
edgecolor="black", label="max_depth=8")
plt.xlim([-6, 6])
plt.ylim([-6, 6])
plt.xlabel("target 1")
plt.ylabel("target 2")
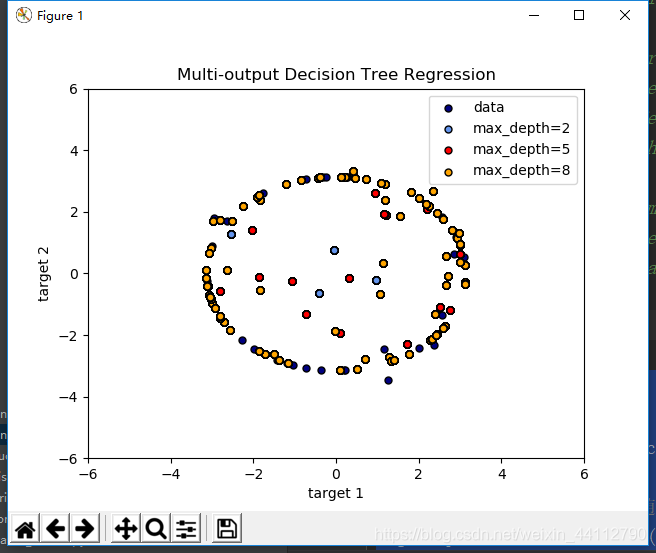
plt.title("Multi-output Decision Tree Regression")
plt.legend(loc="best")
plt.show()
深度为2、5、8的决策树均受到了噪声的干扰,预测的一些结果偏离了圆。
打印决策树信息
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
# 加载数据
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 构造决策树对象进行训练
estimator = DecisionTreeClassifier(max_leaf_nodes=3, random_state=0)
estimator.fit(X_train, y_train)
# The decision estimator has an attribute called tree_ which stores the entire
# tree structure and allows access to low level attributes. The binary tree
# tree_ is represented as a number of parallel arrays. The i-th element of each
# array holds information about the node `i`. Node 0 is the tree's root. NOTE:
# Some of the arrays only apply to either leaves or split nodes, resp. In this
# case the values of nodes of the other type are arbitrary!
#
# Among those arrays, we have:
# - left_child, id of the left child of the node
# - right_child, id of the right child of the node
# - feature, feature used for splitting the node
# - threshold, threshold value at the node
#
# Using those arrays, we can parse the tree structure:
# 提取决策树信息
n_nodes = estimator.tree_.node_count # 节点个数
children_left = estimator.tree_.children_left # 左子树
children_right = estimator.tree_.children_right # 右子树
feature = estimator.tree_.feature # 特征编号
threshold = estimator.tree_.threshold # 临界值
# The tree structure can be traversed to compute various properties such
# as the depth of each node and whether or not it is a leaf.
node_depth = np.zeros(shape=n_nodes, dtype=np.int64) # 构造数组用于填写结点编号
is_leaves = np.zeros(shape=n_nodes, dtype=bool) # 构造数组用于记录是否是叶子
stack = [(0, -1)] # seed is the root node id and its parent depth
while len(stack) > 0:
node_id, parent_depth = stack.pop()
node_depth[node_id] = parent_depth + 1 # 记录结点编号
# If we have a test node
if (children_left[node_id] != children_right[node_id]):
stack.append((children_left[node_id], parent_depth + 1)) # 记录左子树的编号
stack.append((children_right[node_id], parent_depth + 1)) # 记录右子树的编号
else:
is_leaves[node_id] = True # 记录是否为叶子结点
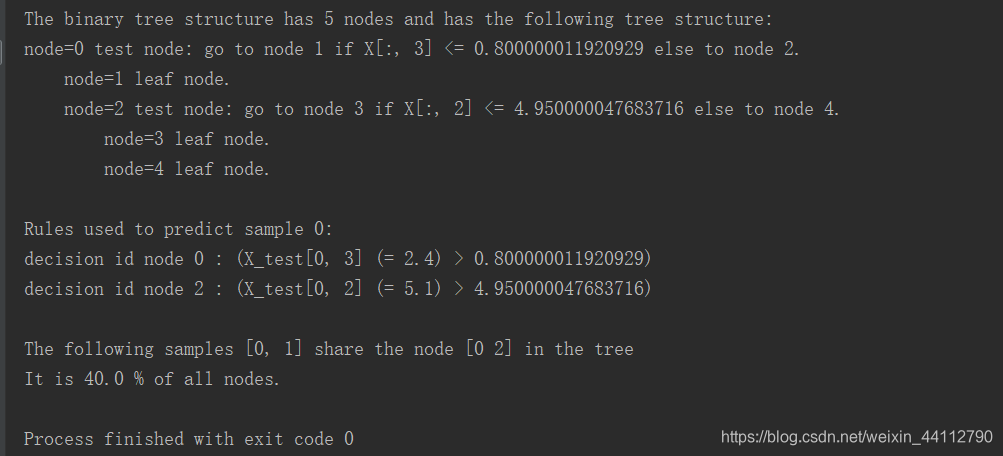
print("The binary tree structure has %s nodes and has "
"the following tree structure:"
% n_nodes)
for i in range(n_nodes):
if is_leaves[i]:
print("%snode=%s leaf node." % (node_depth[i] * "\t", i))
else:
print("%snode=%s test node: go to node %s if X[:, %s] <= %s else to "
"node %s."
% (node_depth[i] * "\t",
i,
children_left[i],
feature[i],
threshold[i],
children_right[i],
))
print()
# First let's retrieve the decision path of each sample. The decision_path
# method allows to retrieve the node indicator functions. A non zero element of
# indicator matrix at the position (i, j) indicates that the sample i goes
# through the node j.
# 节点指示器
node_indicator = estimator.decision_path(X_test)
# Similarly, we can also have the leaves ids reached by each sample.
leave_id = estimator.apply(X_test)
# Now, it's possible to get the tests that were used to predict a sample or
# a group of samples. First, let's make it for the sample.
sample_id = 0
node_index = node_indicator.indices[node_indicator.indptr[sample_id]:
node_indicator.indptr[sample_id + 1]]
print('Rules used to predict sample %s: ' % sample_id)
for node_id in node_index:
# 跳过最终的叶子节点
if leave_id[sample_id] == node_id:
continue
# 判断分叉点
if (X_test[sample_id, feature[node_id]] <= threshold[node_id]):
threshold_sign = "<="
else:
threshold_sign = ">"
# 打印分叉位置的信息
print("decision id node %s : (X_test[%s, %s] (= %s) %s %s)"
% (node_id,
sample_id,
feature[node_id],
X_test[sample_id, feature[node_id]],
threshold_sign,
threshold[node_id]))
# For a group of samples, we have the following common node.
sample_ids = [0, 1]
# 获得两个样本的公共祖先结点
common_nodes = (node_indicator.toarray()[sample_ids].sum(axis=0) ==
len(sample_ids))
# 取出将公共祖先结点的编号
common_node_id = np.arange(n_nodes)[common_nodes]
# 打印两个样本的公共祖先结点编号
print("\nThe following samples %s share the node %s in the tree"
% (sample_ids, common_node_id))
# 计算公共祖先结点占总结点的比例
print("It is %s %% of all nodes." % (100 * len(common_node_id) / n_nodes,))
可以清楚看到决策树的结构,以及各节点分类的特征。
绘制决策树信息
pip install --upgrade scikit-learn升级sklearn才有plot_tree
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
# Load data
iris = load_iris()
# 利用所有特征进行训练并绘制决策树信息
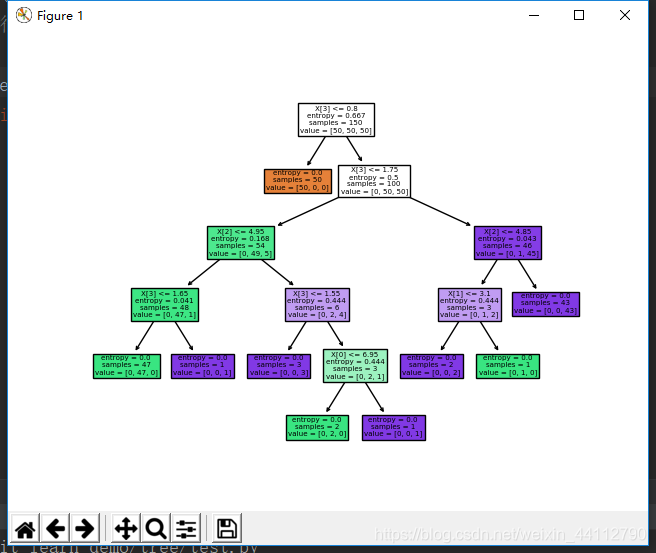
plt.figure()
clf = DecisionTreeClassifier().fit(iris.data, iris.target)
plot_tree(clf, filled=True) # 0.21之前没有,需要升级sklearn.tree
plt.show()
比之前直接打印信息更清晰
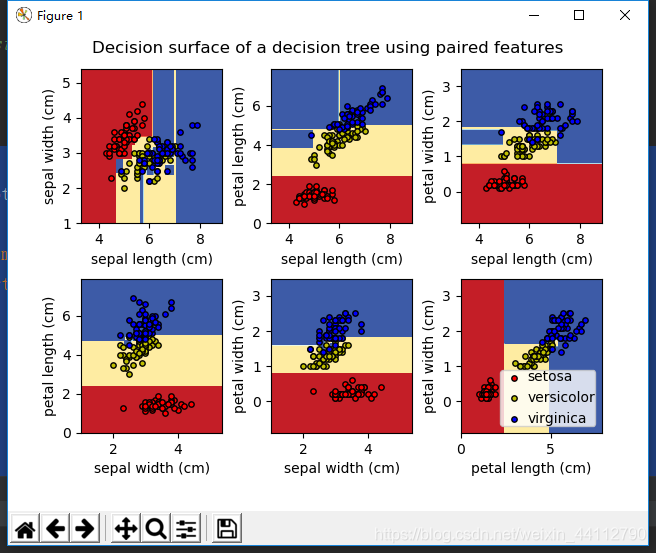
选取部分特征进行预测
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
# Parameters
n_classes = 3
plot_colors = "ryb"
plot_step = 0.02
# Load data
iris = load_iris()
# 4个特征选取2个共6种组合
for pairidx, pair in enumerate([[0, 1], [0, 2], [0, 3],
[1, 2], [1, 3], [2, 3]]):
# We only take the two corresponding features
X = iris.data[:, pair]
y = iris.target
# Train
clf = DecisionTreeClassifier().fit(X, y)
# Plot the decision boundary
# 子图序号
plt.subplot(2, 3, pairidx + 1)
# 构造测设数据的边际
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# 测设数据的网格点坐标
xx, yy = np.meshgrid(np.arange(x_min, x_max, plot_step),
np.arange(y_min, y_max, plot_step))
# 设置边距
plt.tight_layout(h_pad=0.5, w_pad=0.5, pad=2.5)
# 预测np.c_是按行连接两个矩阵,ravel()将矩阵扁平化
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# 将扁平的预测结果展开
Z = Z.reshape(xx.shape)
# 等高线绘制并且填充内部区域
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.RdYlBu)
# 标注用到的特征名字
plt.xlabel(iris.feature_names[pair[0]])
plt.ylabel(iris.feature_names[pair[1]])
# Plot the training points
for i, color in zip(range(n_classes), plot_colors):
# 取出第i类所在位置
idx = np.where(y == i)
# 绘制散点图
plt.scatter(X[idx, 0], X[idx, 1], c=color, label=iris.target_names[i],
cmap=plt.cm.RdYlBu, edgecolor='black', s=15)
# 标注子图信息
plt.suptitle("Decision surface of a decision tree using paired features")
plt.legend(loc='lower right', borderpad=0, handletextpad=0)
plt.axis("tight")
plt.show()