版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
一元线性回归
这里就只取了一个特征的数据直接进行最小二乘法
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
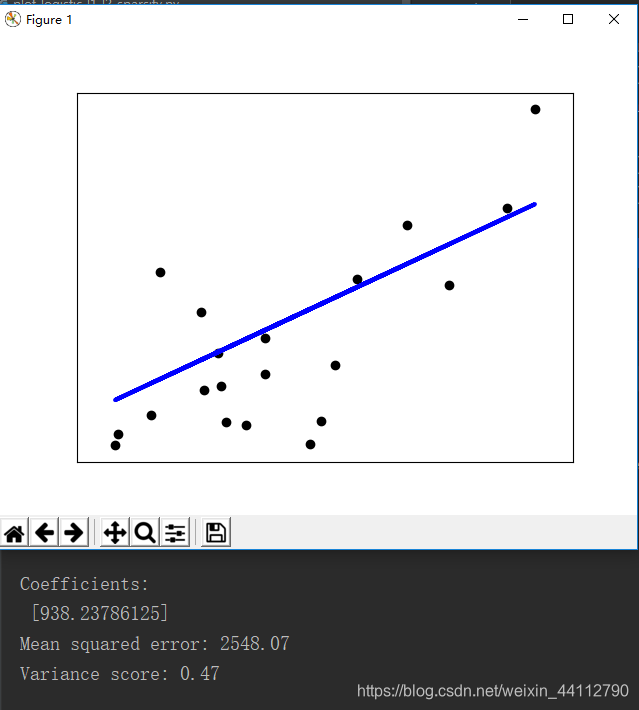
print('Coefficients: \n', regr.coef_)
# The mean squared error
print("Mean squared error: %.2f"
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
最后绘制的回归直线
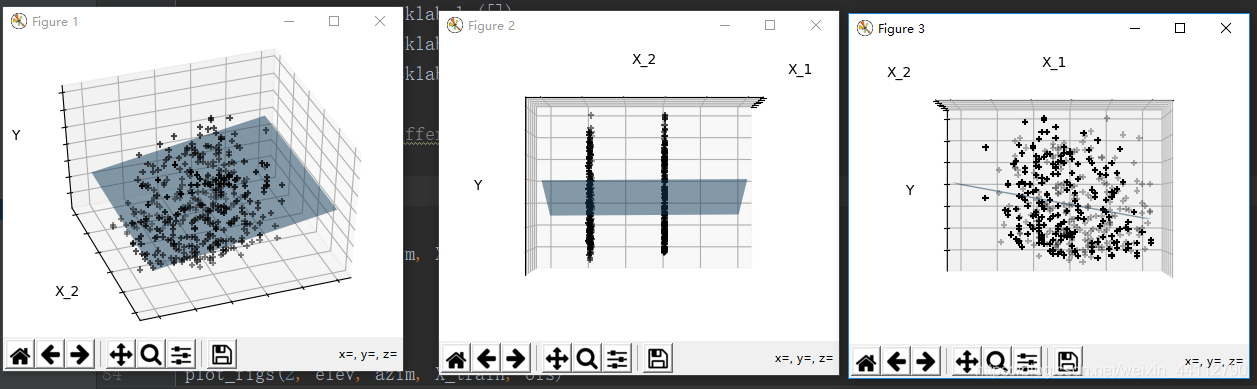
二元线性回归
这个案例演示了如何绘制二元线性回归结果的图像,
diabetes = datasets.load_diabetes()
# 特征的索引,只用了两个特征
indices = (0, 1)
# 前面作为训练集,最后20个作为测试集
X_train = diabetes.data[:-20, indices]
X_test = diabetes.data[-20:, indices]
y_train = diabetes.target[:-20]
y_test = diabetes.target[-20:]
# 构造线性回归对象
ols = linear_model.LinearRegression()
# 训练
ols.fit(X_train, y_train)
# #############################################################################
# Plot the figure
def plot_figs(fig_num, elev, azim, X_train, clf):
'''
:param fig_num: 绘图编号
:param elev: float,方位角视角
:param azim: float,高程视角
:param X_train: 训练集
:param clf: 回归器对象
:return:
'''
# 采取独立的绘图窗格,而不是子图
fig = plt.figure(fig_num, figsize=(4, 3))
# 清空绘图窗格
plt.clf()
# 构造3D坐标对象 azim : float,方位角视角,默认为-60。lev : float,高程视角,默认为30。
ax = Axes3D(fig, elev=elev, azim=azim)
# 绘制离散点
ax.scatter(X_train[:, 0], X_train[:, 1], y_train, c='k', marker='+')
# 预测数据绘制平面
ax.plot_surface(np.array([[-.1, -.1], [.15, .15]]),
np.array([[-.1, .15], [-.1, .15]]),
clf.predict(np.array([[-.1, -.1, .15, .15],
[-.1, .15, -.1, .15]]).T
).reshape((2, 2)),
alpha=.5)
# 标注横纵轴信息
ax.set_xlabel('X_1')
ax.set_ylabel('X_2')
ax.set_zlabel('Y')
ax.w_xaxis.set_ticklabels([])
ax.w_yaxis.set_ticklabels([])
ax.w_zaxis.set_ticklabels([])
#Generate the three different figures from different views
# 以不同的视角进行绘图
elev = 43.5
azim = -110
plot_figs(1, elev, azim, X_train, ols)
elev = -.5
azim = 0
plot_figs(2, elev, azim, X_train, ols)
elev = -.5
azim = 90
plot_figs(3, elev, azim, X_train, ols)
plt.show()
从不同的视角绘制出了最小二乘拟合的平面和数据集
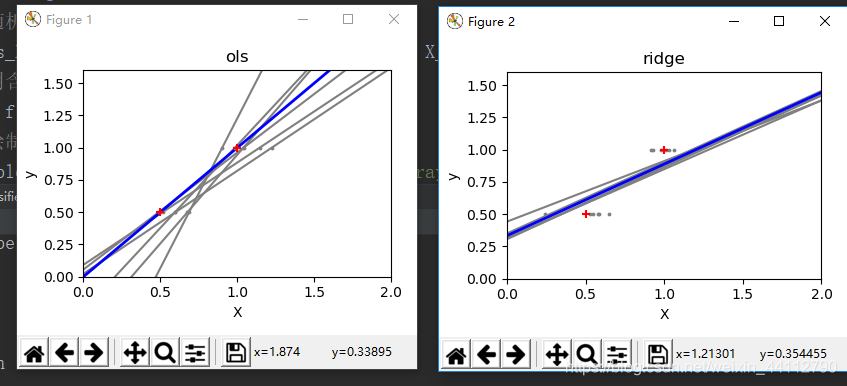
与岭回归对比
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# 构造数据,这里就是取了(0.5, 0.5) (1, 1)这两个点做线性回归
X_train = np.c_[.5, 1].T
y_train = [.5, 1]
X_test = np.c_[0, 2].T
# 随机数种子
np.random.seed(0)
# 构造模型字典用于循环,从而减少代码量
classifiers = dict(ols=linear_model.LinearRegression(),
ridge=linear_model.Ridge(alpha=.1))
# 遍历字典,训练、预测并绘图
for name, clf in classifiers.items():
# 获得绘图画布、坐标轴
fig, ax = plt.subplots(figsize=(4, 3))
for _ in range(6):
# 随机噪声扰动
this_X = .1 * np.random.normal(size=(2, 1)) + X_train
# 用含噪声的数据集训练
clf.fit(this_X, y_train)
# 绘制预测结果直线
ax.plot(X_test, clf.predict(X_test), color='gray')
# 绘制含噪声的训练集离散点
ax.scatter(this_X, y_train, s=3, c='gray', marker='o', zorder=10)
# 用原数据集训练
clf.fit(X_train, y_train)
# 绘制预测结果直线
ax.plot(X_test, clf.predict(X_test), linewidth=2, color='blue')
# 绘制训练集离散点
ax.scatter(X_train, y_train, s=30, c='red', marker='+', zorder=10)
# 标注绘图信息
ax.set_title(name)
ax.set_xlim(0, 2)
ax.set_ylim((0, 1.6))
ax.set_xlabel('X')
ax.set_ylabel('y')
fig.tight_layout()
plt.show()
面对噪声岭回归并没那么敏感,斜率较为稳定(右图);而普通的最小二乘法求解的线性回归斜率却不稳定,