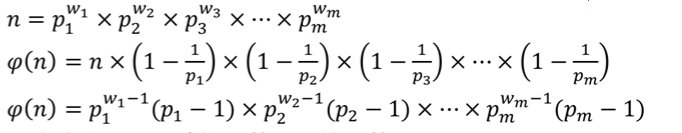1.计数
题目描述
给定n,m,k都是小于10001的正整数,输出给定的n个数中,其m次幂能被k整除的数的个数。
输出满足条件的数的个数。
输入
两行组成,第一行是n,m,k。
第二行是n个正整数,不超过10001.
输出
输出满足条件的数的个数。
样例输入
3 2 50
9 10 11
样例输出
1
解题思路
还是比较水了,我们算一下时间复杂度,发现只要n方再优化一下就没有问题了,于是,快速幂就可以过了。说不定数据水还可以暴力
2.弹药科技
题目描述
经过精灵族全力抵挡,精灵终于坚持到了联络系统的重建,于是精灵向人类求助,
大魔法师伊扎洛决定弓}用博士的最新科技来抗敌。
伊扎洛:“博士,还没好吗?”
博士:“只差一步了!只需要在正确的位置装上弹药就可以了!”
博士的最新科技是全新的炸弹,但是现在还需要一步装弹药的操作。博士的炸弹有
N!个位置可以装弹药(>.<),但是只有在正确的位置装上弹药才能启动,博士将
装弹药的位置编号为1到N!,一个位置i需要装弹药,当且仅当gcd(i, N!) ≠ 1且
N! mod i ≠ 0,现在博士不要求你求出所有装弹药位置,只需要你求出满足要求
的位置的数量就可以了。
输入
一个数N
输出
表示满足要求的位置数量,答案对mod1000000007输出
样例输入
4样例输出
9解题思路
首先,确定我们就是在1到n!之中统计数,所以呢,答案就是这其中总数减去不符合条件的数。
有哪些数不符合条件呢?
1.n!的约数
2.与n!互质的数。
那么思路就很明显了,答案就是n!-n!的约数个数-1到n中与n互质的数。
但我们会发现1被算了两次,于是加上1.
那么这道题就比较水了。
1.求n!的约数个数
当然,是有公式的。
则
于是我们就求出来的。
2.求1到n中与n互质的数
就是n欧拉函数的值
我们需要对n!进行质因数分解。于是就运用以上两个公式就可以求了。至于用哪种全凭个人喜好。
值得注意的是,如用第一种,除数取模要用到逆元。
其实我们会发现欧拉函数是一个积性函数,那么
于是我们可以求出所有的欧拉函数的值,一直乘即可。
但这一种方法是错的。我们再回顾一下积性函数的定义
由于保证不了互质,因此就不能这样做。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<queue>
#include<vector>
#include<algorithm>
#define mod 1000000007
using namespace std;
int n,phi[1000005],pri[500000],cnt;
bool vis[1000005];
long long tmpphi[1000005],tmp,sum[1000005];
long long qkpow(long long x,long long y){
long long ans = 1;
while (y){
if (y & 1)
ans = ans * x % mod;
x = x * x % mod;
y /= 2;
}
return ans;
}
int main(){
phi[1] = 1;
for (int i = 2;i <= 1000000;i ++){
if (!vis[i]){
phi[i] = i - 1;
pri[++ cnt] = i;
}
for (int j = 1;j <= cnt && 1ll * i * pri[j] <= 1000000;j ++){
vis[i * pri[j]] = 1;
if (i % pri[j] == 0){
phi[i * pri[j]] = phi[i] * pri[j];
break;
}
else
phi[i * pri[j]] = phi[i] * (pri[j] - 1);
}
}
scanf ("%d",&n);
long long phis = 1;
long long tmp = 1;
for (int i = 1;i <= n ;i ++)
tmp = tmp * i % mod;
for (int i = 1;i <= cnt && pri[i] <= n;i ++)
for (long long j = pri[i];j <= n;j *= pri[i])
sum[i] += n / j;
for (int i = 1;i <= cnt ;i ++){
if (!sum[i])
continue;
phis = phis * qkpow(pri[i],sum[i] - 1) % mod * (pri[i] - 1) % mod;
}
long long y = 1;
for (int i = 1;i <= cnt;i ++)
y = y * (sum[i] + 1) % mod;
long long ans = (tmp + mod - phis + mod - y + 1) % mod;
printf("%lld",ans);
}3.数列
题目描述
有一个数列,满足两个性质:
1. 数列中任意两端相邻且长度相等的部分不完全相同,比如3 6 3 6 是不合法的。
2. 该数列是左右满足条件1的数列中字典序最小的。给出一个整数N,求数列的第N项。
3. 数列为正整数(震惊!)
输入
一个整数N
N<=
输出
一个数,表示数列的第N项。
样例输入
20样例输出
3
解题思路
恩...题目都不懂,数据还这么大,那怎么做?
题目意思其实大家都理解,但怎么做到呢。对于此类题目,我们姑且尝试推一推,至少推一下说不定就找到规律了。
1| 2| 1 3| 1 2 1 4 |1 2 1 3 1 2 1 5 |1 2 1 3 1 2 1 4 1 2 1 3 1 2 1 6
于是不难发现,这是有规律的,
第一次是1,那么第二个就是 2 为 1 + 1;
第二次构造 已有数列1 2
构造数列 1 3 为 1 2 + 1.
第三次构造 已有数列 1 2 1 3
构造数列 1 2 1 4 为 1 2 1 3 + 1.
第四次构造 已有数列 1 2 1 3 1 2 1 4
构造数列 1 2 1 3 1 2 1 5 为 1 2 1 3 1 2 1 4 + 1
于是就是将已有数列复制过来加一个1就可以了。
那么不也就是位就是x。
但如果n不是2的x幂就需要新处理了。
由于是copy的,我们会发现,这是否有些像分治,一直二分下去能求到解。
并且,我们一下余数的关系。
1所在的是(n%2=1)
2所在的是(n%2%2=1)
3所在的是(n%2%2%2=1)
那么x 所在的就是 (n%2%2...%2(x次)=1)
于是我们可以一直取模,一直到1那么就到了头,中间模的就相当于是所累加的,于是可以得到答案。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#include<map>
#include<cstdlib>
using namespace std;
char s[10005];
int a[10005],ans,b[1005];
int main(){
scanf ("%s",s + 1);
int lens = strlen(s + 1);
for (int i = 1;i <= lens;i ++)
a[i] = s[i] - '0';
while (1){
ans ++;
if (a[lens] % 2 == 1){
printf("%d",ans);
return 0;
}
memset(b,0,sizeof(b));
int xx = 0;
for (int i = 1;i <= lens;i ++){
b[i] = (xx * 10 + a[i]) / 2;
xx = (xx * 10 + a[i]) % 2;
}
for (int i = 0;i <= lens;i ++)
a[i] = b[i];
}
}4.gcd
题目描述
给定整数N,求1<=x,y<=N且Gcd(x,y)为素数的数对(x,y)有多少对?
输入
一个整数
1<=N<=10000000
输出
一个整数
样例输入
4样例输出
4解题思路
我做过,但好像没啥印象,不得不说很久以前的题还是记不住。
但考场居然还是差不多推出来了,就一个前缀和优化没打。主要就是我看那数据估计不会超时,谁知数据多了一个0.(粗鄙的借口)
首先一个简明扼要的思路肯定是要通过区间内的所有素数来进行操作。
但每一个素数所做的贡献如何统计呢。
合数与合数有些也符合条件例如(9,24).
我们看一下,9 = 3 * 3 ,24 = 3 * 8
因为3 8 互质,因此可以这样搞。
所以说...
枚举素数3,到了3 * 8的时候,就应该累加phi(8).
那么你想一下,岂不是就暴力了...
考场当场刚了出来
for (int i = 1;pri[i] <= n && i <= cnt;i ++){
sum ++;
for (long long j = 1ll * pri[i] * 2;j <= n;j += pri[i]){
sum = sum + (phi[j / pri[i]] * 2);
}
}结果数据多了一个0,超时了。
于是我们又发现,从1到n/pri[i]我们都累加了phi。肯定,中间有重复的,于是我们用前缀和优化即可。
于是又比较水了。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#include<map>
#include<cstdlib>
using namespace std;
int n,pri[670000],cnt,phi[10000005];
bool vis[10000005];
long long sumphi[10000005];
int main(){
//freopen("gcd.in","r",stdin);
//freopen("gcd.out","w",stdout);
scanf ("%d",&n);
phi[1] = 1;
for (int i = 2;i <= 10000000;i ++){
if (!vis[i]){
pri[++ cnt] = i;
phi[i] = i - 1;
}
for (int j = 1;j <= cnt && 1ll * i * pri[j] <= 10000000;j ++){
vis[i * pri[j]] = 1;
if (i % pri[j] == 0){
phi[i * pri[j]] = phi[i] * pri[j];
break;
}
else
phi[i * pri[j]] = phi[i] * (pri[j] - 1);
}
}
for (int i = 1;i <= n ;i ++)
sumphi[i] = sumphi[i - 1] + phi[i];
long long sum = 0;
for (int i = 1;pri[i] <= n && i <= cnt;i ++){
sum += sumphi[n / pri[i]] * 2 - 1;
}
printf("%lld\n",sum);
}总结
总体来看代码好像并不复杂...但确实是难想到正解。考试暴力都打不出来,可以说很可怕了....
但其实看到了题解,我就可以很轻松地做出来,不得不说考试的时候真的难上加难。