旅行商问题(TSP) --- 蛮力法(深度优先遍历算法DFS),贪心算法,动态规划
问题描述
TSP问题(Traveling Salesman Problem,旅行商问题),由威廉哈密顿爵士和英国数学家克克曼T.P.Kirkman于19世纪初提出。问题描述如下:
有若干个城市,任何两个城市之间的距离都是确定的,现要求一旅行商从某城市出发必须经过每一个城市且只在一个城市逗留一次,最后回到出发的城市,问如何事先确定一条最短的线路已保证其旅行的费用最少?
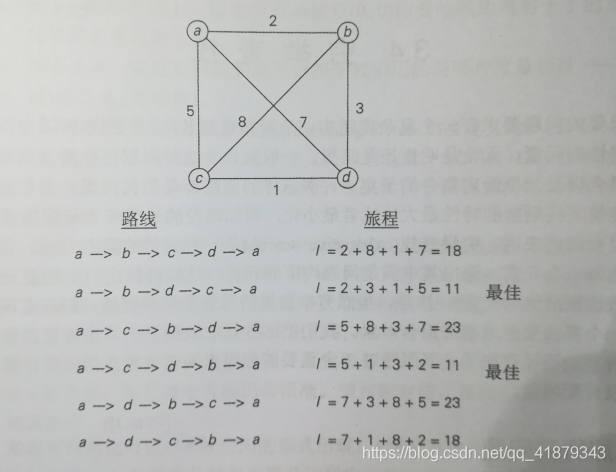
蛮力法(深度优先遍历算法DFS)
通过遍历出所有满足条件的路径情况,并保持更新最优解,直到所有情况都遍历完,得到全局最优解。但是,使用蛮力法需要遍历的城市个数高达n的阶乘,当n=12的时候,需遍历479001600种情况,程序所需时间以小时为单位。
代码演示:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
#define maxx 9999
int l[maxx][maxx];//存储两个城市之间的距离
int n;//城市数量
int min_l = maxx;//最短路径
int sum[maxx];//标记每条路线的路程总长度
int go_city;//标记从第go_city个城市出发
int visited[maxx]; //第i个城市已经去过:visited[i]=1;反之则为visited[i]=0;
int path_index = 1; //已经去过的城市数目。
int path[maxx][maxx];//存储经过城市的路线
int route = 0;//存储第几条路线
int recursion(int index)
{
if(path_index != n)
{
for(int i=1;i <= n;i++)
{
if(visited[i] == 0)
{
visited[i] = 1;
path[route][path_index] = index;
path_index++;
recursion(i);
//回溯
path_index--;
visited[i] = 0;
}
}
}
else
{
//路线中加上最后一个城市和第一个城市(需要返回到最初的城市)
path[route][path_index] = index;
path[route][path_index + 1] = go_city;
//计算每条路线的路程总长度,并输出路线
printf("路线%d为:\n",route+1);
sum[route] = 0;
for(int i=1;i<=n;i++)
{
sum[route] += l[ path[route][i] ][ path[route][i+1] ];
cout << path[route][i] << " --> ";
//当route+1后,path[route][i]的前面需要保持,后面变化。
path[route+1][i] = path[route][i];
}
if(min_l > sum[route])
{
min_l = sum[route];
}
cout << path[route][n+1] << endl;
cout << "该路线总长度为: " << sum[route] << endl;
route++;
}
return 0;
}
int main()
{
memset(visited,0,sizeof(visited));
cout << "请输入城市数量:";
cin >> n;
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
printf("请输入%d号城市到%d号城市之间的距离:",i,j);
cin >> l[i][j];
l[j][i] = l[i][j];
}
}
cout << "请输入您出发的城市是第几个城市:";
cin >> go_city;
visited[go_city] = 1;
recursion(go_city);
cout << "最短路程长度为: ";
cout << min_l << endl;
return 0;
}
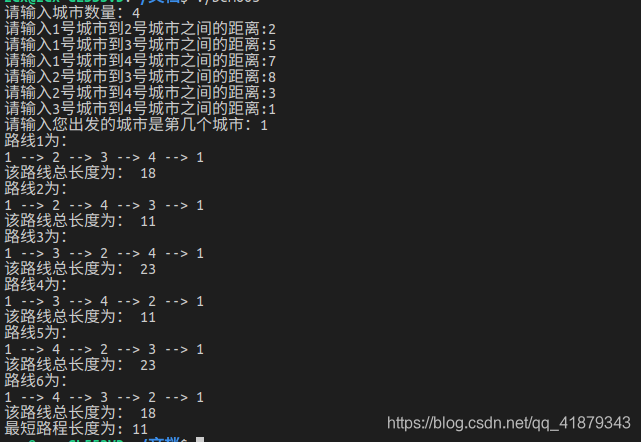
代码运行结果如下:
贪心算法
贪心算法:又称贪婪算法(greedy algorithm),该算法是指:在对问题求解时,总是做出当前情况下的最好选择,否则将来可能会后悔,故名“贪心”。这是一种算法策略,每次选择得到的都是局部最优解。选择的策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
针对TSP问题,使用贪心算法的求解的过程为:
- 从某一个城市开始,每次选择一个城市,直到所有的城市被走完。
- 每次在选择下一个城市的时候,只考虑当前情况,保证迄今为止经过的路径总距离最小。
#include <iostream>
#include <cstdio>
#include <cstring>
#define maxx 9999
using namespace std;
int n;//城市总数量
int l[maxx][maxx];//标记两两城市之间的距离
int go_city;//初始出发的城市
int visited[maxx];//标记是否已经走过,visited[i]=1为走过,=0为未走过
int min_l = 0;//最小总路程
int greedy(int index)
{
cout << "路线为:" << endl;
cout << index << " --> ";
//已经确定从第go_city号城市出发,所以只需要在确定n-1个城市
for(int i=1;i<n;i++)
{
int len = maxx;
int j_j;
for(int j=1;j<=n;j++)
{
if(visited[j] != 0)
{
continue;
}
//筛选与当前城市距离最短的城市,并标记
if(len > l[index][j])
{
len = l[index][j];
j_j = j;
}
}
index = j_j;
cout << index << " --> ";
//标记j_j号城市已走过。
visited[j_j] = 1;
min_l += len;
}
//加上最后一个城市到go_city城市的距离
min_l += l[index][go_city];
cout << go_city << endl;
return 0;
}
int main()
{
memset(visited,0,sizeof(visited));
cout << "请输入城市数量:";
cin >> n;
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
printf("请输入%d号城市到%d号城市之间的距离:",i,j);
cin >> l[i][j];
l[j][i] = l[i][j];
}
}
cout << "请输入您出发的城市是第几个城市:";
cin >> go_city;
visited[go_city] = 1;
greedy(go_city);
cout << "最短路程长度为: ";
cout << min_l << endl;
return 0;
}
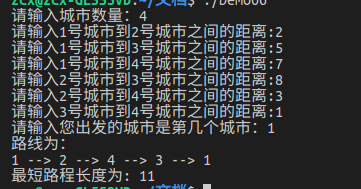
运行结果如下:
动态规划
保存的数都是不重复的比较小的整数,所以这里用二进制串表示集合。比如集合{1,3,5,6,7}表示成二进制串用1110101,其中集合里面有的数对应的位数写成1,没有的写成0。要判断第3位是不是1,就把 1110101右移(3-1)位,得到11101,然后结果和00001进行 & 运算,如果结果是1说明第3位是1,否则说明第3位是0。
- 推广一下,对于数字x,要看它的第i位是不是1,那么可以通过判断布尔表达式 (((x >> (i - 1) ) & 1) == 1的真值来实现。
对于下面这个测试用例,图和邻接矩阵如下,不能走的话用0表示,实际存储的时候用一个比较大的数字,比如0x7ffff:
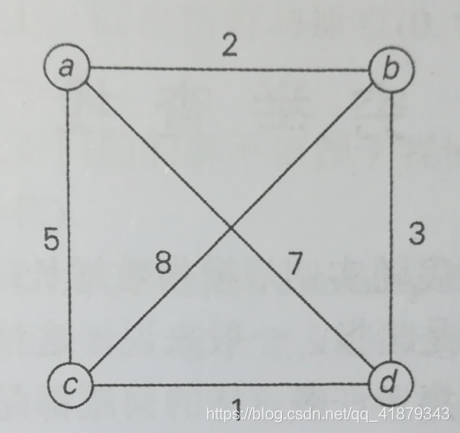
要使用动态规划,需要问题本身有最优子结构,我们需要找到要解决的问题的子问题。
题目要求,从0(a)出发,经过[1(b),2©,3(d)]这几个城市,然后回到0,使得花费最少。要实现这个要求,需要从下面三个实现方案中选择花费最少的方案。
- 从0出发,到1,然后再从1出发,经过[2,3]这几个城市,然后回到0,使得花费最少。
- 从0出发,到2,然后再从2出发,经过[1,3]这几个城市,然后回到0,使得花费最少。
- 从0出发,到3,然后再从3出发,经过[1,2]这几个城市,然后回到0,使得花费最少。
可以发现,三个小的解决方案的最优解,构成了大的解决方案,所以这个问题具有最优子结构,可以用动态规划来实现。
设置一个二维的动态规划表dp,定义符号{1,2,3}表示经过[1,2,3]这几个城市,然后回到0。
设置一个二维数组l保存两个城市之间的距离。
那么题目就是求dp[0][{1,2,3}]。将{1,2,3}表示成二进制,就是111,对应10进制的7,所以题目是在求dp[0][7];
要求三个方案的最小值意味:
- dp[0][{1,2,3}] = min{l[0][1]+dp[1][{2,3}] ,l[0][2]+dp[2][{1,3}] ,l[0][3]+dp[3][{1,2}]}
- dp[1][{2,3}] = min{ l[1][2]+dp[2][{3}] ,l[1][3]+dp[3][{2}]}
- dp[2][{3}] = l[2][3]+dp[3][{}]
- dp[3][{}]就是从3出发,不经过任何城市,回到0的花费,所以dp[3][{}] = l[3][0]
先确定一下dp表的大小,有n个城市,从0开始编号,那么dp表的行数就是n,列数就是2^(n-1),即1 << (n – 1),集合{1,2,3}的子集个数。在求解的时候,第一列的值对应这从邻接矩阵可以导出,后面的列可以有前面的列和邻接矩阵导出。所以求出的动态规划表就是:
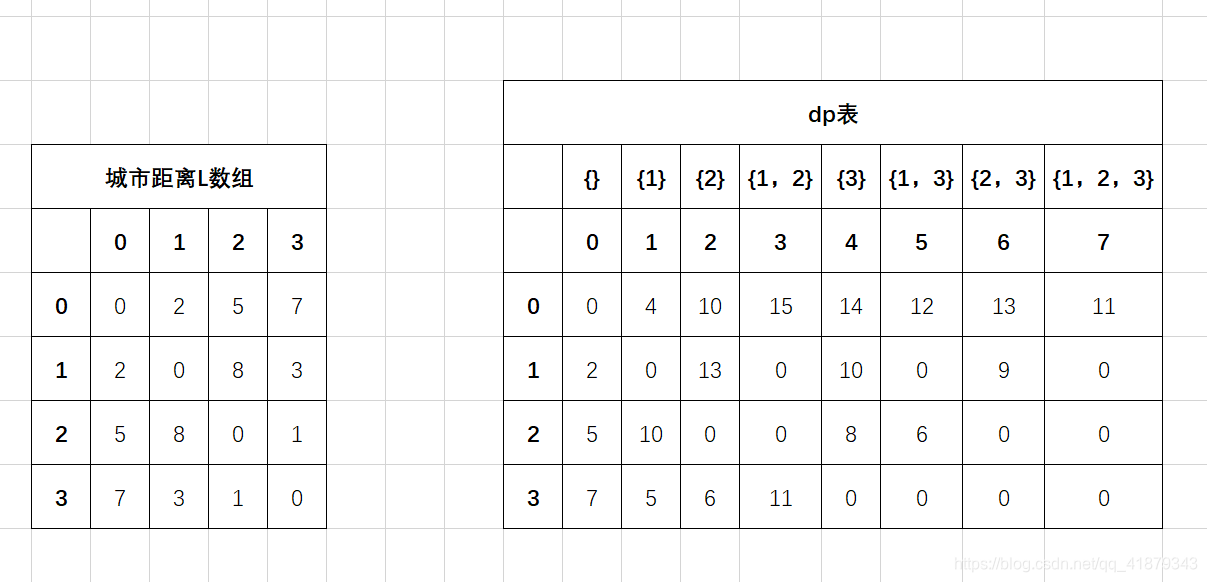
当J=0时,第一轮循环只需:
for(int i =0;i <n;i++)
{
dp[i][0] = l[i][0];
}
第二轮就需要带入l和dp了:
j = 1;
for(int i = 0;i < n;i++)
{
dp[i][j] = l[i][1]+dp[1][0];
}
后面的规律比较麻烦的一点在于要集合和二进制转换,观察发现:
- dp[2][5] 表示从2出发,通过{1,3},最后回到起点。那么:
- dp[2][5] = min{l21 + dp[1][{3}],l23 + dp[3][{1}]} = min{l21 + dp[1][4],l23 + dp[3][1]} ;
- 从2出发,要去{1,3}。
- 先看去1的路,去了1集合{1,3}中只剩下{3} ,{3}对应4,所以要求的dp表就是dp[1][4],这个4可以通过(101) ^ (1)得到,(1) = 1<<(1-1)
- 再看去2的路,5 = 101的第二位是0,所以不能去2。判断第二位为1,用(5>>(2-1)) &1==1。而且也由于从2出发,就更不能去了。
- 最后看去3的路,去了3集合{1,3}中只剩下{1},{1}对应这1,所以要求的dp表就是dp[3][1],1通过(101) ^ (100)得到。(100) = 1<<(3-1)
- 同样求dp[0][7] = min{l[0][1] + dp[1][6], l[0][2]+ dp[2][5],l[0][3] + dp[3][3]}
- 从0出发,要去{1,2,3}
- 先看去1的路,去1然后去6 = {2,3},6通过(111) ^ (1)得到,(1) = 1<<(1-1)
- 再看去2的路,去2然后去5 = {1,3},5通过(111) ^ (10)得到。(10) = 1<<(2-1)
- 最后看去3的路,去3然后去3 = {1,2},3通过(111) ^ (100)得到。(100) = 1<<(3-1)
- 还要注意,求dp[2][3]的时候。就是求从2出发,经过{1,2},显然不合理,在dp表中应为0。对于这种情况,只用判断数字3的二进制位的第2位是不是1,是1就表示不合理。
根据以上的推导,最后求TSP问题的完整解法就是:
//旅行商问题:动态规划
#include <iostream>
#include <cstdio>
#include <cstring>
#define maxx 10000
using namespace std;
int n;//城市数量
int l[maxx][maxx];//城市之间的距离
int dp[maxx][maxx];//dp表
int menthod()
{
//给第一列赋值
for (int i = 0; i < n; i++)
{
dp[i][0] = l[i][0];
}
//给其他列赋值
for (int j = 1; j < 1 << (n - 1); j++)
{
for (int i = 0; i < n; i++)
{
dp[i][j] = 0x7ffff; //表示无穷大
//判断是否走过该城市j,如果走过了,就continue
if (j >> (i - 1) & 1)
{
continue;
}
for (int k = 1; k < n; k++)
{
//通过位运算判断是否需要经过k城市,不能经过k城市就continue
if ((j >> (k - 1) & 1) == 0)
{
continue;
}
//获取dp[i][j]的最小值,(l[i][k] + dp[k][j ^ (1 << (k - 1))这个在思路上有解释
if (dp[i][j] > (l[i][k] + dp[k][j ^ (1 << (k - 1))]))
{
dp[i][j] = l[i][k] + dp[k][j ^ (1 << (k - 1))];
}
}
}
}
return 0;
}
int main()
{
memset(dp, 0, sizeof(dp));
cout << "请输入城市数目:";
cin >> n;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
printf("请输入第 %d 号城市到第 %d 号城市之间的距离:", i, j);
cin >> l[i][j];
l[j][i] = l[i][j];
}
}
menthod();
cout << "最短路径为: " << dp[0][(1 << (n - 1))-1] << endl;
return 0;
}
