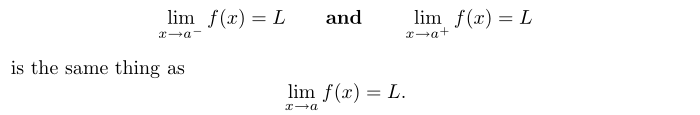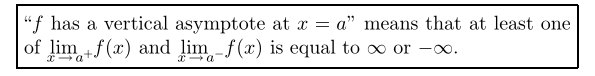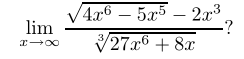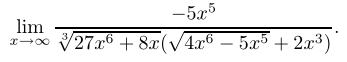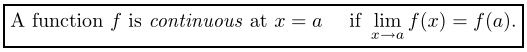普林斯顿微积分读本小记（未完待续）

本文所有图片均引用自班纳教授普林斯顿微积分读本
中文内容则是博主自己的一些见解和抄录

第一章 函数图像和直线

1.1.4 垂线检验

函数是一一映射的，如果一个 $f(x)$对应两个值，那么就不是函数
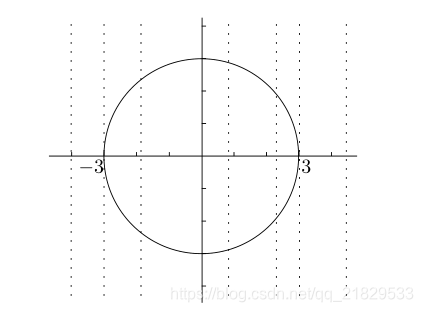
垂线检验便是如此，如果一个图形与同一条垂直于 $x$轴的直线有两交点，那么就没有通过垂线检验，不是函数。
如上图，一条与 $x$轴垂直的直线 $x=1$与曲线 $x^2+y^2=9$有两个交点
所以 $x^2+y^2=9$不通过垂线检验，即 $x^2+y^2=9$不是函数

1.2.1 水平线检验

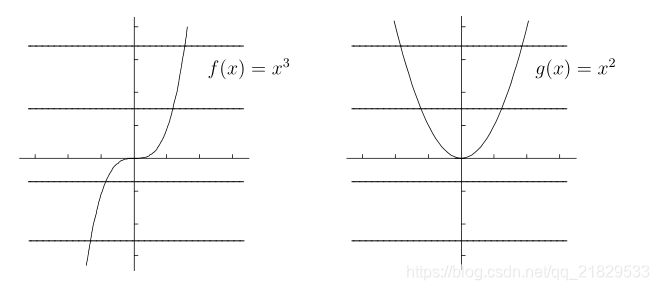
一个函数存在反函数当且仅当存在每一个 $y=f(x)$仅与一个 $x$对应。
由此引入水平线检验
即每条水平线仅与函数图像有一个交点的时候， 该函数才存在反函数
如上图的左图

1.3 复合函数

$f(x)=g(h(x))$ 记为 $f=g○h$
$f(x)=g(x)h(x)$ 记为 $f=gh$
$g(x)=x^2,h(x)=sin(x)$
$g○h=(sin(x))^2$
$gh=x^2sin(x)$

1.4 奇函数和偶函数

偶函数沿 $y$轴对称

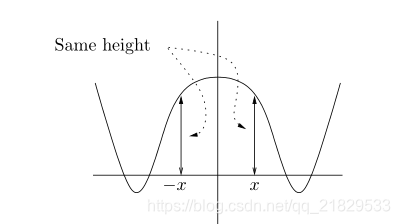
奇函数沿原点中心对称

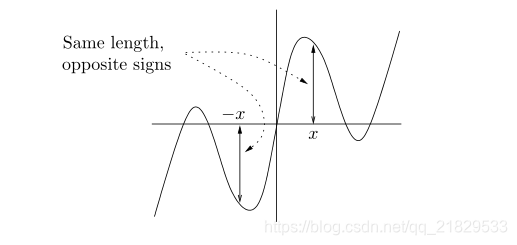
检验是奇函数还是偶函数的方法：
$f(-x)=-f(x)$ 奇函数
$f(x)=f(-x)$ 偶函数

1.6 常见函数

(1)多项式

$f(x)=ax^n+bx^{n-1}...$

(2)有理函数

$f(x)=\frac{g(x)}{h(x)}$ 其中 $g(x)、h(x)均为多项式$

(3)指数函数和对数函数

$f(x)=b^x$ 指数函数
$f(x)=log_{b}(a)$ 对数函数

(4)三角函数

$f(x)=sin(x)/cos(x)/tan(x)...$

(5)带有绝对值的函数

$f(x)=|x|$

第二章 三角学回顾

2.4 三角恒等式

$sin^2(x)+cos^2(x)=1$
$1+tan^2(x)=sec^2(x) \rightarrow sec^2(x)-tan^2(x)=1$
$1+cot^2(x)=csc^2(x)\rightarrow csc^2(x)-cot^2(x)=1$

和差角公式
$sin(a+b)=sin(a)cos(b)+sin(b)cos(a)$
$cos(a+b)=cos(a)cos(b)-sin(a)sin(b)$
$sin(a-b)=sin(a)cos(b)-sin(b)cos(a)$
$cos(a-b)=cos(a)cos(b)+sin(a)sin(b)$

倍角公式
$sin(2x)=2sin(x)cos(x)$
$cos(2x)=cos^2(x)-sin^2(x)=2cos^2(x)-1=1-2sin^2(x)$

第三章 极限导论

3.2 左极限和右极限

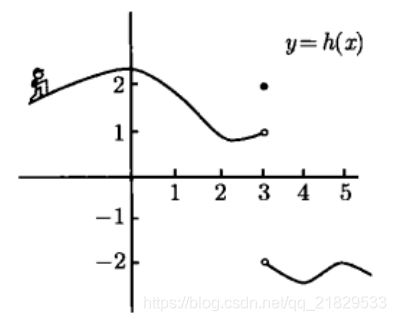
左极限： $\lim_{x \to3^-}h(x)=1$
右极限： $\lim_{x \to3^+}h(x)=-2$
双侧极限： $\lim_{x \to3}h(x)=DNE$
左极限与右极限相等时存在双侧极限

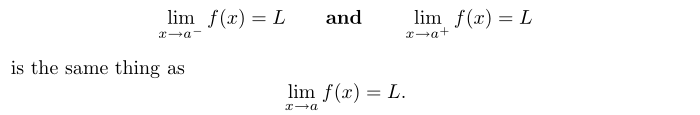
3.3&3.4 垂直渐近线和水平渐近线

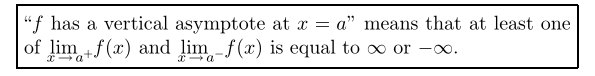
3.6 三明治定理

众所周知，这个定理还有这另一个神奇的名字。
$-1\leq sin(x)\leq-1$
两边同乘一个 $x$可得
$-x\leq xsin(x) \leq x$

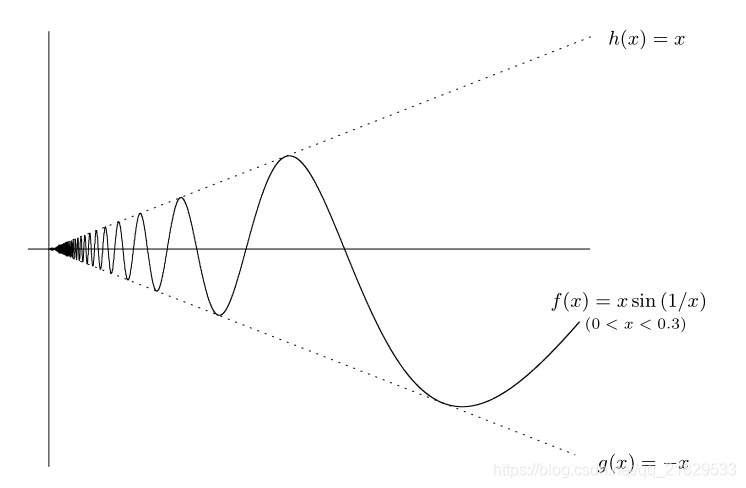
$x=0,f(x)=x,f(x)=0$
$x=0,f(x)=-x,f(x)=0$
因此可以求出 $xsin(x)$在 $0$处的极限
$\lim_{x \to 0}xsin(x)=0$

第四章 求解多项式的极限问题

比较有意思的一道题

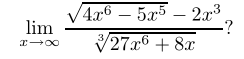
主要的问题是只看最大项的话上面会消掉
做法是上下同乘以上方的共轭表达式 $\sqrt{4x^6-5x^5}+2x^3$
整理后得到

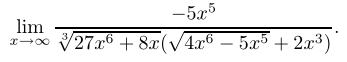
这个时候就可以只看最大项了
$\lim_{x\to \infty} 原式=\lim_{x \to \infty} \frac{-5x^5}{3x^2*(2x^3+2x^3)}=\lim_{x \to \infty} \frac{-5x^5}{12x^5}=\frac{-5}{12}$

第五章 连续性和可导性

5.1 连续性

5.1.1一点处的连续

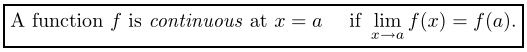
一个函数在某一个点连续，要满足一下几点
1.双侧函数 $\lim_{x\to a}f(x)$存在，a有限
2.f(a)存在，a有限
3.以上两个量相等

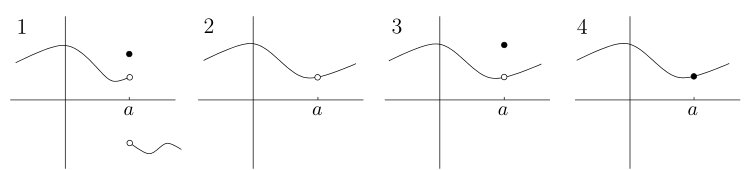
上图第一个不存在双侧极限
第二个 $f(a)$不存在
第三个双侧极限与 $f(a)$不相等
上三张图的 $a$点均被称为不连续点

5.1.2 区间连续

一个函数在 $[a,b]$上连续
1. $(a,b)$处处连续
2. $a$处右极限等于 $f(a)$，也称在 $x=a$处右连续
3. $b$处左极限等于 $f(b)$，也称在 $x=b$处左连续

5.1.4 介值定理

这玩意应该就是高中里的零点存在定理
如果连续区间 $[a,b]$满足 $f(a)*f(b)<0$则 $[a,b]$中至少存在一个零点。

比如说可以证明 $f(x)=cos(x)$与 $f(x)=x$有交点

这只需要证明 $f(x)=cos(x)-x$有零点就行了

5.1.6 最大值和最小值定理

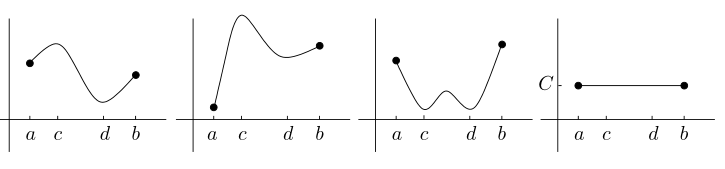
连续函数至少有一个最大值和一个最小值

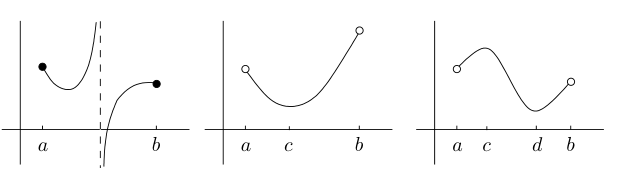
第三张需要特别注意
尽管这不是一个连续函数，但它仍然有最大值和最小值。