机器学习小白第一周自我总结

自己的总结

机器学习第一周：线性回归

监督学习和非监督学习，自己的理解是

• 监督学习
  监督学习就像被人带着学习，给你很多的样本，用大量的样本建成一个模型，从而可以通过自己的数据用已经训练好的模型去预测接下来要发生的事。
• 非监督学习
  非监督学习自然就是，没有之前通过很多数据建成的模型，只能自己去搞，然后将数据集合分成由类似的对象组成的多个类 。比如将同类型的新闻，聚在一起，然后很多种新闻被分成一类一类的。

单变量线性回归

监督学习肯定需要一个样本集合，单变量就是指其只有一个变化特征，此时需要一个假设函数hypothesis （其实就是我们通过特征估出来的值）
$h(x) = θ_0+θ_1X$
其中θ就是对于这个假设函数最合适的参数，X是指特征的指。

要选择出最适合的参数θ，就需要用到代价函数 ----- $J(θ_0,θ_1)$

$J(θ_0,θ_1) = \frac{1}{2m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})^2$

代价函数的作用就是选择出最适合的参数，即使得J最小时的 $θ_0,θ_1$
(就是说为了算出我们想要的目标函数的值，需要知道目标函数的参数θ，怎么知道θ呢，用代价函数，当代价函数最小的时候，θ值最合适)

如何找到代价函数J的最小值？

此时就需要用到下一种算法 梯度下降

梯度下降的作用便是，通过一步一步的走，最终找出代价函数 $J(θ_0,θ_1)$的最小值。前面说了找出代价函数的最小值之后就知道，最适合的θ值，然后就能求出目标函数值。

梯度下降的公式： $θ_j :=θ_j - α\frac{\phi}{\phi\theta_j}J(θ_0,θ_1)$对于单变量线性回归 $h(x) = θ_0+θ_1x$ 此时 j = 0 and j = 1. 其中α是学习率,相当于一步一步走的时候,步子迈多大,梯度下降时,需要同步的更新 $θ_0,θ_1$的值,
因此: $temp0 =θ_0 - α\frac{\phi}{\phi\theta_0}J(θ_0)$ $temp1 =θ_1 - α\frac{\phi}{\phi\theta_1}J(θ_1)$ $θ_0 := temp0$ $θ_1 := temp1$
如果学习率α太大,就会导致一次步子迈太大性错过最低点,从而不能收敛,甚至发散

接下来就是将梯度下降算法带入代价函数
$\frac{\phi}{\phi\theta_j}J(θ_0,θ_1) = \frac{1}{2m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})^2$
当j = 0时: $θ_0 := θ_0 - α\frac{1}{m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})*x^{(0)}$ 此时暂且令x^(0) 为1 因为这样不会对目标函数起到改变(x0*θ0).
当j = 1时: $θ_ 1:= θ_1 - α\frac{1}{m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})*x^{(1)}$

多变量线形回归

多变量线形回归就是指,我们的目标函数拥有多个特征.我们可以把一个训练集的特征看做一个矩阵
比如一间房子的房价Y ,由面积,房间数量,楼层决定.假设售价10000元,面积1平米,两间房,3层楼.X[1,2,3] (大概这意思)
上文提到令x^(0) 为1 所以此时的假设函数 $h(x) = θ_0X_0+θ_1X_1+θ_3X_3+θ_4X_4........+θ_nX_n$

其中x表示不同的特征,而theta就表示不同特征的不同参数

此时假设函数相当于一个一行n列的θ矩阵和一列n行的x矩阵相乘,可记为 $h(x) = θ^TX$

同样的

单变量梯度下降是为了找出使得代价函数最小值的那 一个 参数 多变量梯度下降是为了找出使得代价函数最小的 一系列 参数θ0,θ1, θ2, θ3…

$θ_j :=θ_j - α\frac{\phi}{\phi\theta_j}J(θ_0,θ_1,θ_2.....θ_n)$
带入多变量的代价函数,求导之后可得 $θ_0 := θ_0 - α\frac{1}{m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})*x^{(0)}$
$θ_1 := θ_1 - α\frac{1}{m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})*x^{(1)}$
$θ_2 := θ_2 - α\frac{1}{m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})*x^{(2)}$
$θ_n := θ_n - α\frac{1}{m}\sum_{i=1}^{m}(h(X^{(i)}) - y^{(i)})*x^{(n)}$

总结: 单变量梯度下降是为了找出使得代价函数最小值的那一个参数 多变量梯度下降是为了找出使得代价函数最小的一系列参θ0,θ1,θ2,θ3…

但是一步一步的走,若样本特征数量很多,就会走很久.

此时采用特征缩放的方法使得特征相对减少,运行速度变快.
特征缩放就是令 $x_n = \frac{x_n-\mu_n}{s_n}$
其中 $\mu_n代表$训练样本集该特征的平均值, $s_n$表示该特征的标准差,也可以直接用最大值减去最小值

如: 一间房子的面积特征为 0~~2000 此时该特征缩放为 $x=\frac{x-平均值}{2000-0}$

学习率

学习率不能大,一般α采用 0.01 0.03 0.1 0.3 1 3 10

代价函数的值 与迭代次数和学习有关 可以构造图像 看代价函数迭代多少次趋于平稳 看迭代次数的多少判断学习率大或小

特征可以自己定义,带入不同的特征和参数,得出多变量回归方程(参数用多变量梯度下降和代价函数共同找到)

正规方程

正规方程可直接得出使得代价函数最小的参数
$θ =(X^TX)^{-1}X^TY$
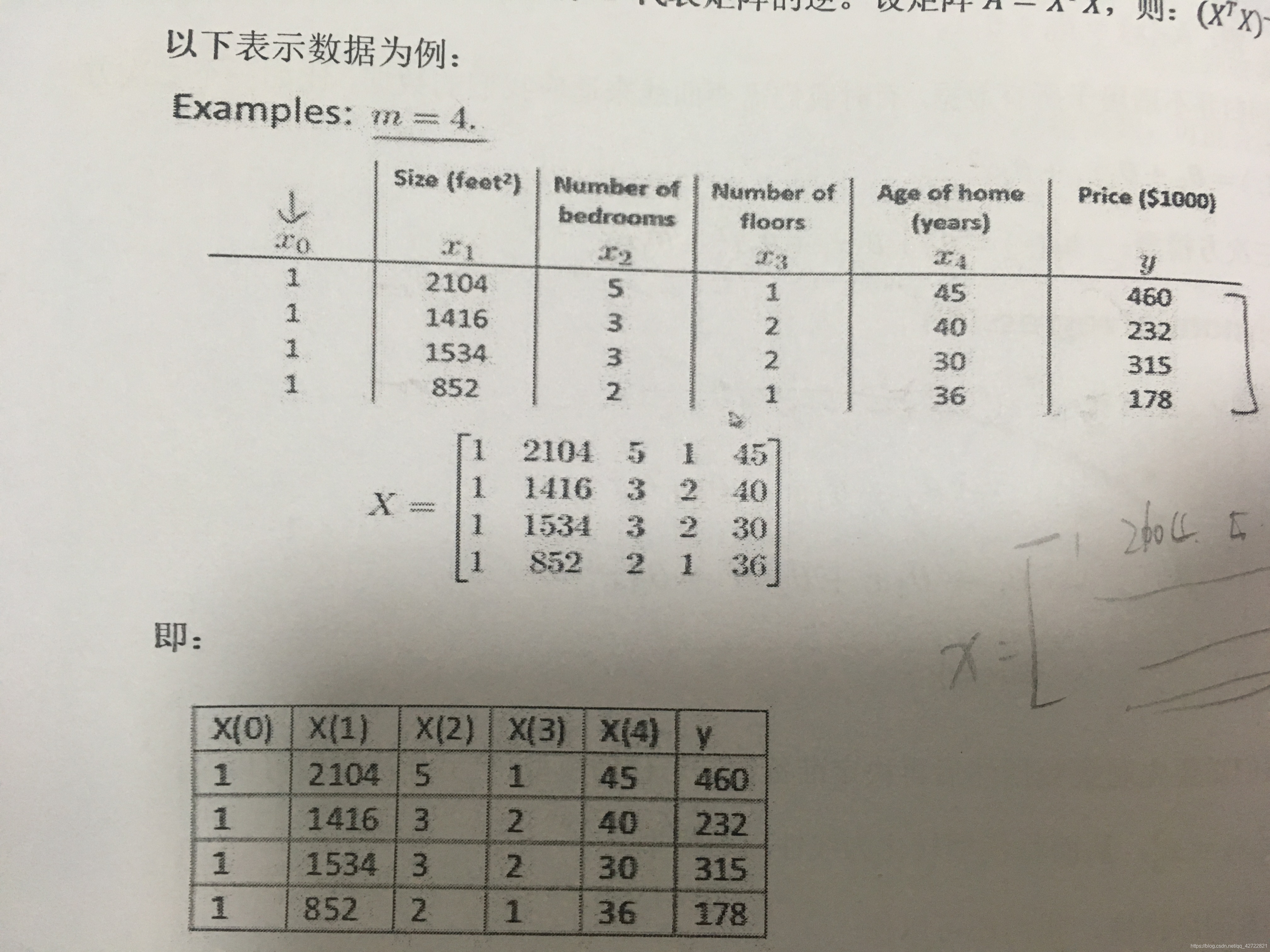
其中X表示将所有特征集和的一个矩阵

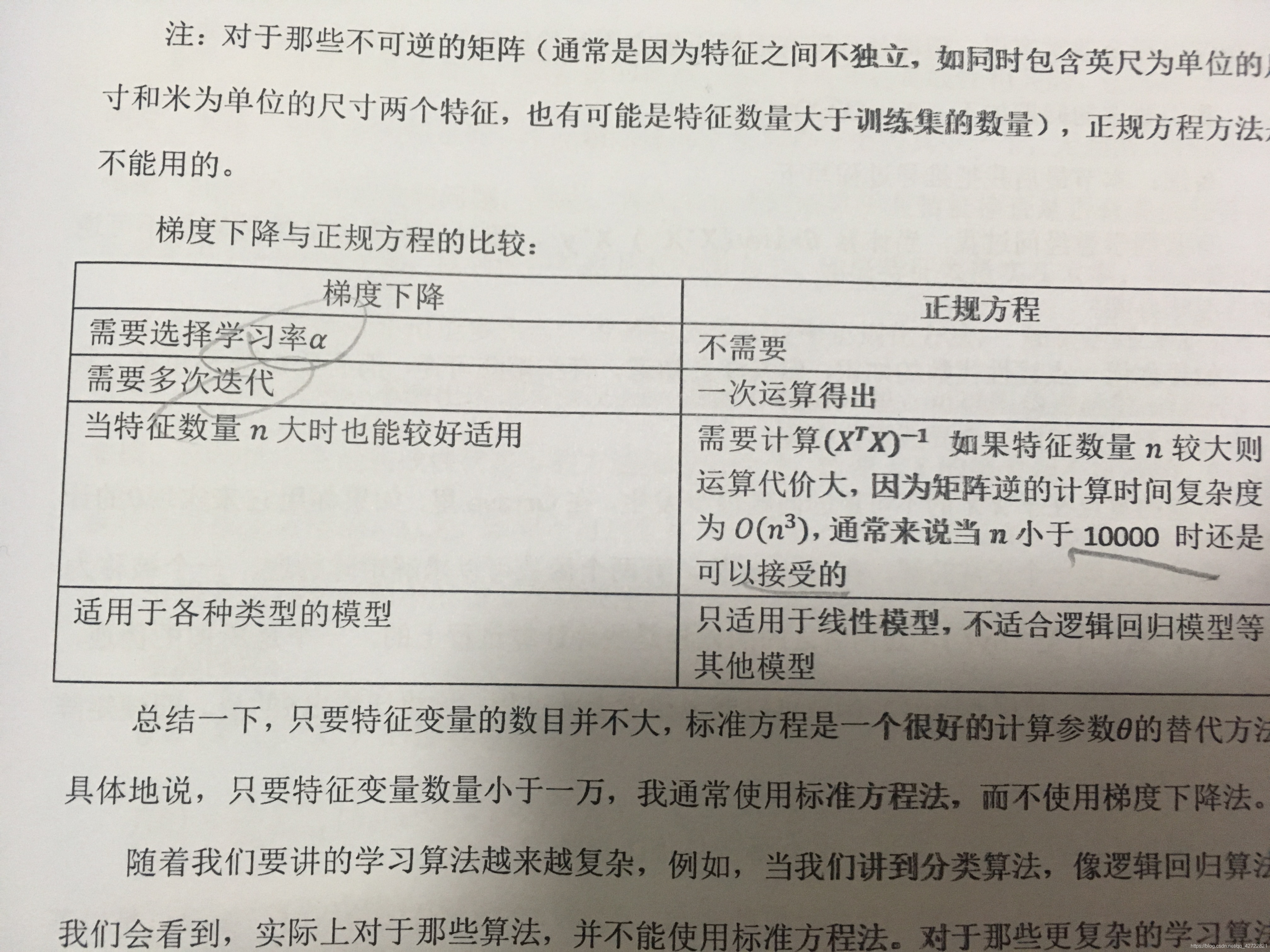
梯度下降和正规方程的比较