2-8、蒙特卡洛模拟

一、背景

蒙特卡罗模拟方法 (Monte Carlo simulation) 诞生于上个世纪40年代美国的”曼哈顿计划”，名字来源于赌城蒙特卡罗。蒙特卡罗算法从某种意义上而言，就是一种赌博算法。
它是一种基于随机试验和统计计算的数值方法，也称计算机随机模拟方法或统计模拟方法。蒙特卡罗方法的数学基础是概率论中的大数定律和中心极限定理。

二、算法引入

最早接触到这类算法应该是在高中或者初中阶段，而且是一道送分题。即在一个正方形中有一个内接圆。现在在这个正方形内抛洒豆子。已知正方形面积为S，落在正方形内的豆子总数为 $M$ ，其中落在内接圆内的豆子总数为 $N$ 。请估算内接圆的面积。

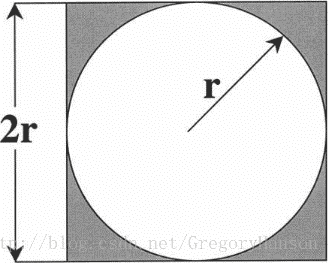
根据概率论中的大数定律可知，当随机事件发生的次数足够多的时候（趋向于正无穷），其发生频率就可作为此事件发生的概率。对于本题，当抛洒的豆子足够多的时候，落在圆中的豆子比值即可视为圆与正方形面积的比值。那么计算结果 $S× N/M$ 即为圆形面积。
这种算法需要承担一定的风险，但是比起这种算法带给我们的收益，风险其实不足为惧，同时我们也可以运用合理恰当的方式来最小化这种风险。
在建模和仿真中，应用蒙特卡罗方法主要有两部分工作：用蒙特卡罗方法模拟某一过程时，产生所需要的各种概率分布的随机变量；用统计方法把模型的数字特征估计出来，从而得到问题的数值解，即仿真结果。

解题步骤如下：
1、根据提出的问题构造一个简单、适用的概率模型或随机模型，使问题的解对应于该模型中随机变量的某些特征（如概率、均值和方差等），所构造的模型在主要特征参量方面要与实际问题或系统相一致。
2、根据模型中各个随机变量的分布，在计算机上产生随机数，实现一次模拟过程所需的足够数量的随机数。通常先产生均匀分布的随机数，然后生成服从某一分布的随机数，方可进行随机模拟试验。
3、根据概率模型的特点和随机变量的分布特性，设计和选取合适的抽样方法，并对每个随机变量进行抽样（包括直接抽样、分层抽样、相关抽样、重要抽样等）。
4、按照所建立的模型进行仿真试验、计算，求出问题的随机解。
5、统计分析模拟试验结果，给出问题的概率解以及解的精度估计。

三、算法应用

蒙特卡罗算法的应用领域很多，这个算法在金融学、经济学、工程学等领域得到了广泛应用。适用于 $Monte-Carlo$ 算法的问题，比较常见的有两类。一类是问题的解等价于某事件的概率，如算法引入中提到的求解圆的面积问题。另一类是判定问题，即判定某个命题是否为真，例如主元素存在性判定和素数的测试问题。
对于第一类算法所涉及到的问题，最多的就是定积分的求解。通常情况下我们有公式来求解各种图形的面积，当然也可以求解定积分。但是当我们遇到不规则图形以及极为复杂难以求解的定积分时，由于定积分的直观意义就是函数曲线与 $x$ 轴围成的图形中， $y>0$ 的面积减去 $y<0$ 的面积。同样是对于不规则面积的求解，最终我们都可以回到蒙特卡罗算法中来求解面积。

对于蒙特卡罗算法，其优缺点也是比较明显的:
优点：
1、能够比较逼真的描述具有随机性质的事物的特点及物理实验过程
2、受几何条件限制小
3、收敛速度与问题的维数无关
4、误差容易确定
5、程序结构简单，易于实现
缺点：
1、收敛速度慢
2、误差具有概率性
3、进行模拟的前提是各输入变量是相互独立的

四、算法实例

例1:

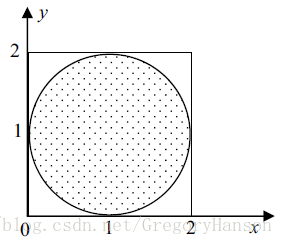
在不知道求解圆面积的公式的情况下，试用蒙特卡罗法求出圆面积。

解答：
由上文介绍可知，可在matlab中生成大量在 $[0;2]$ 上服从均匀分布的随机数，从而模拟上文中的抛撒豆子。通过计算落在圆中的点与总点数，就可算出圆与正方形面积之比。

%Monte-Carlo
sita = 0:0.01:2*pi;
x = sin(sita);
y = cos(sita);%计算半径为1的圆周上的点,以便做出观察
m = 0;%计数器
x1 = 2*rand(1000,1) - 1;
y1 = 2*rand(1000,1) - 1;
N = 1000;%设置实验次数
for n = 1:N
    p1 = x1(1:n);
    q1 = y1(1:n);
    if (x1(n) * x1(n) + y1(n) * y1(n)) < 1
        m = m + 1;
    end
    plot(p1,q1,'.',x,y,'-k',[-1 -1 1 1 -1],[-1 1 1 -1 -1],'-k');
    axis equal;
    axis([-2 2 -2 2]);
    text(-1,-1.2,['实验总次数 n=',num2str(n)]); %显示实验结果
    text(-1,-1.4,['落入圆中数 m=',num2str(m)]);
    text(-1,-1.6,['近似圆面积 S_c=',num2str(m/n*4)]);
    set(gcf,'DoubleBuffer','on'); %双缓冲避免作图闪烁
    drawnow; %显示结果
end

为了提升程序效率，可以取消仿真过程中间的可视化显示，并且利用 $Matlab$ 的矩阵运算来改造程序。
修改后代码如下：


ti                          % 计时器启动
n=10000;                    % 每次随机落点10000个
for k=1:1000                % 重复试验1000次
    x1=2*rand(n,1)-1;
    y1=2*rand(n,1)-1;       % 随机落点产生
    m(k)=sum((x1.*x1+y1.*y1)<1);% 求落入圆中的点数和
end
S_c=mean(m).*4./n           % 计算并显示结果
time=toc                    % 显示耗时

此例题方法可扩展到求解不规则图形面积等问题上。求解所得结果会有很小的偏差，当生成的随机点数足够多时，此误差可忽略不计。

例2:
用蒙特卡洛法求解积分 $\int_0^6 \frac 1 3xdx$ 。

求解：

clear
clc
n=10000;
tol=[];
for i=1:10000
    x1=6*rand(n,1);
    y1=2*rand(n,1);
    tol(i)=sum(x1.*(1/3)>y1);
end
S=mean(tol).*12./n;

口算该积分值可得答案为6。如果用蒙特卡罗算法计算，撒10000个点可得到值为6.0007，误差仅为0.0007，相对于6这个结果已经可以忽略不计。
该代码中每次计算撒了10000个点。蒙特卡罗算法得到的解的准确率会随着撒点次数的增大而提升，这是蒙特卡罗算法的优点同时也是它的弊端。当仿真情形过于复杂时，若要得到一个比较精确的结果，大量的模拟次数会使程序运行时间过长。所以何时使用蒙特卡罗算法要从多方面考虑，蒙特卡罗算法在硬件配置的约束下，并不是一种万能解法。

当然数学建模比赛中并不大可能直接要你求解某个不规则图形的面积。很多的算法理解起来或者运用起来并不难，多数难点在于，队员能否发现某个问题与某种算法是契合的。也就是能否让人发出“我X，这个算法还能这样用啊！”的感叹。蒙特卡罗算法也是一样。

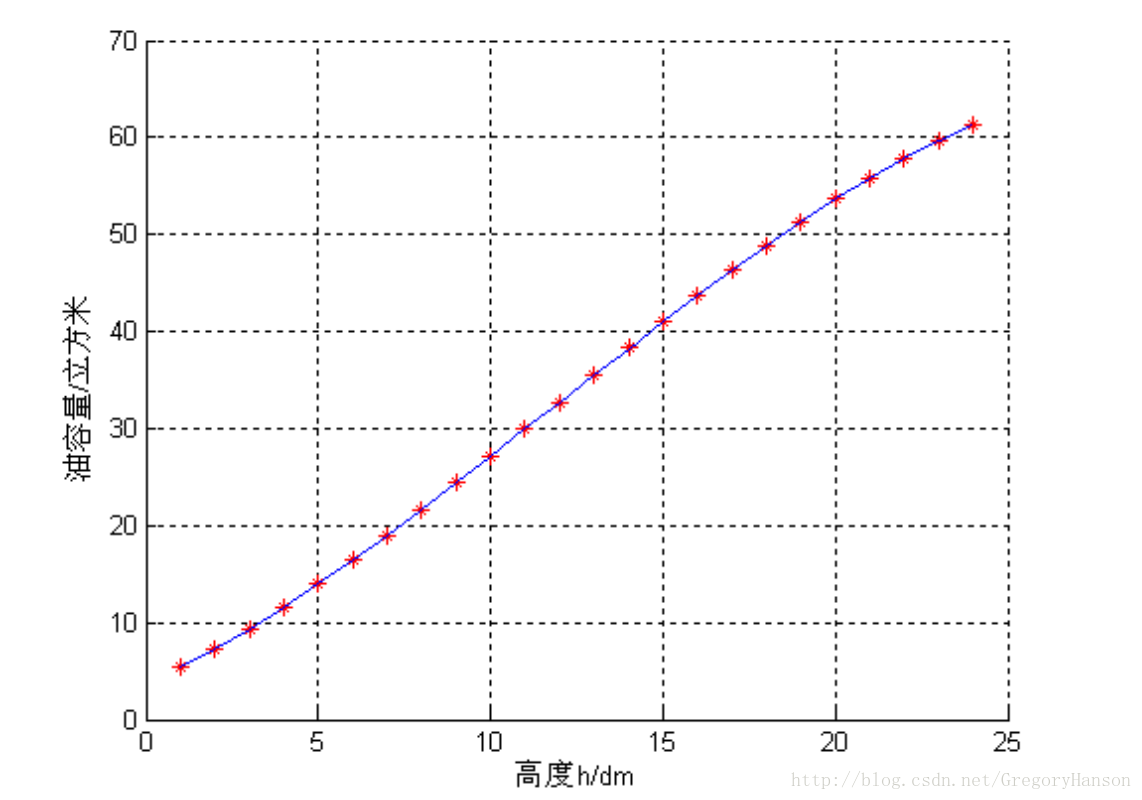
灵活运用蒙特卡罗算法的一个比较经典的例子就是2010年国赛A题的储油罐问题了。有兴趣的朋友可以自行查找原题，这里不对题目再做赘述。
以下是网上一篇优秀论文在该题中利用蒙特卡罗法解题的方式。

六模型的检验与评价
6.1 模型的检验（蒙特卡洛模拟方法）
在实际储油罐罐容表模型的建立和求解过程中，我们对球冠体内倾斜的部分燃油的体积进行了近似计算，忽略了一小部分球冠体体积。鉴于此，我们考虑通过用计算机模拟对该部分的体积进行模拟计算，观察近似计算值与精确模拟数值的吻合情况，同时也对我们建立的模型进行验证。
模拟过程中的主要步骤：

Step1: 划分空间，确定被忽略区域 $Q$ 的空间限制范围，建立空间限制函数表达式。并寻求一包含该区域 $Q$ 的最小长方体。建立坐标系，确定 $Q$ 所在的区域范围；
Step2: 均匀做点，在长方体内分别从 $x,y,z$ 三个坐标轴依次等间距的产点 $p_i (x_i, y_i, z_i)$ ，记录落入该区域的点以及生成的点的总数 $M$ ，计算该长方体区域的总体积 $V$ ；
Step3: 统计落在该区域的点的个数，求该部分体积 $V_Q$ ，计算公式为：
$V_{Q} = \frac{m}{M} * V$ $V_Q =\frac m M* V$

在模拟中对不同区域分别进行求解所忽略部分的体积 $V_Q$ ,再与所得到的理论值相加可得实际测量的精确值。根据蒙特卡洛模拟得到的被省略部分的体积，我们可以画出实际体积和近似体积的差别图。

该论文非常巧妙的将蒙特卡罗算法用于模型的检验而不是用于模型的求解，灵活的利用了蒙特卡罗算法的特性，得到了较优的结果。

五、算法扩展——拉斯维加斯算法

蒙特卡罗是一类随机方法的统称。这类方法的特点是，可以在随机采样上计算得到近似结果，随着采样的增多，得到的结果是正确结果的概率逐渐加大，但在（放弃随机采样，而采用类似全采样这样的确定性方法）获得真正的结果之前，无法知道目前得到的结果是不是真正的结果。
拉斯维加斯方法是另一类随机方法的统称。这类方法的特点是，随着采样次数的增多，得到的正确结果的概率逐渐加大，如果随机采样过程中已经找到了正确结果，该方法可以判别并报告，但在但在放弃随机采样，而采用类似全采样这样的确定性方法之前，不保证能找到任何结果（包括近似结果）。
有兴趣的同学可以查找资料进行深入了解。

本文参考了以下链接的文章：
http://blog.sina.com.cn/s/blog_5396207a0102wgkc.html
蒙特卡罗算法关联的拉斯维加斯算法引用
http://www.ruanyifeng.com/blog/2015/07/monte-carlo-method.html
关于蒙特卡罗算法的部分实例
http://www.360doc.com/content/11/0518/19/991597_117736089.shtml
关于蒙特卡罗算法更多应用实践参考