一、解析VAR
当在分析方法中计算风险价值(VAR)时,我们需要假设金融工具的返回遵循一定的概率分布。最常用的是正态分布,这也是为什么我们通常称它为delta normal方法。要计算VAR,我们需要找到一个阈值(T),来确定显著性(如95%、99%、99.9%)。使用函数F的标准正态累计分布:

将逆累积分布函数应用到1-α:
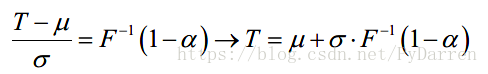
虽然我们不知道非正态分布的累积函数和它的逆的数学公式,但我们可以用计算机来解决这个问题。用R来计算苹果股票的95%,1天的VaR,使用的是delta normal方法,基于两年的数据集。据估计,苹果收益率的平均值和标准差分别为0.13%和1.36%。代码如下:
Apple <- read.table("Apple.csv", header = T, sep = ";")
r <- log(head(Apple$Price,-1)/tail(Apple$Price,-1))
m <- mean(r)
s <- sd(r)
VaR1 <- -qnorm(0.05, m, s)
print(VaR1)
[1] 0.02110003
阈值T,也就是VAR,可以通过下式求出,注意要取绝对值,因为VAR被解释为一个正数:

VAR(95%,1天)为2.11%,这意味着,苹果股价在一天内不会下跌超过2.11%的可能性为95%。从相反的角度来说,苹果的股票在一天损失超过2.11%的概率为5%。
下表显示了苹果公司历史VAR值的实际分布情况:
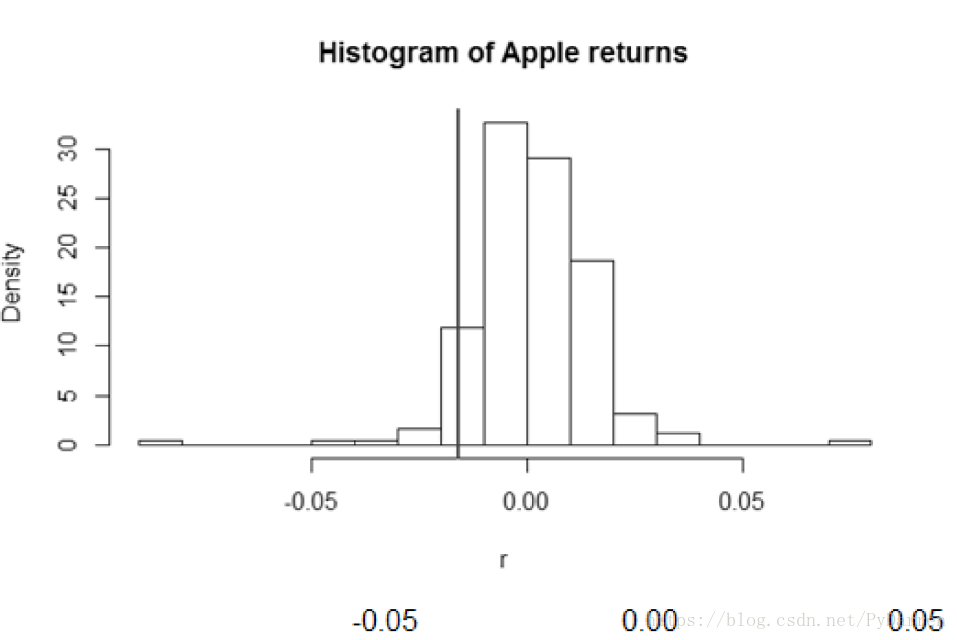
二、历史模拟法
计算风险价值最简单的方法是历史模拟法。这里需要假设金融工具的历史回报率等于期望回报率。因此,我们需要找到α值部分的阈值。在统计中,这被称为百分数。例如,如果我们使用95%显著水平的VAR,那么它意味着数据集中较低第五百分位数。代码如下:
VaR2 <- -quantile(r, 0.05)
print(VaR2)
5%
0.01574694
将此应用于Apple股票,我们得到1.57%的较低第五百分位数。风险值是此百分位数的绝对值。因此,我们可以说苹果股票在一天内损失超过1.57%的可能性为5%,或者股票损失率低于1.57%,可能性为95%。
三、蒙特卡洛模拟
蒙特卡洛模拟法是计算VAR最复杂的方法,一般在其他方法不能使用的情况下才值得使用,原因有问题的复杂性或难以假设其概率分布。
蒙特卡洛模拟可用于金融及其他学科的许多不同领域。基本方法是建立一个模型并假设外生变量的分布。接着根据假定的分布随机生成模型的输入数据,然后收集结果并得出结论。当得出模拟输出的数据后,我们可以按照与历史模拟法相同的步骤进行操作。
使用10000次蒙特卡洛模拟来计算苹果的风险价值看起来似乎有些矫枉过正,这里仅作为示范。代码如下:
sim_norm_return <- rnorm(10000, m, s)
VaR3 <- -quantile(sim_norm_return, 0.05)
print(VaR3)
5%
0.02128257
我们得到的风险价值为2.13%,这与deltar normal方法得出的结论2.11%非常接近,这并不是巧合。两者都遵循收益率符合正态分布的假设,因此,差异来自于模拟的随机性,模拟采取的步骤越多,结果越接近deltar normal方法,蒙特卡洛模拟方法的修正是假设分布基于金融工具的历史数据的历史模拟。这里数据的生成并不是基于数学函数,而是基于历史数据随机选择的,最好是基于独立同分布方法。
对苹果股票使用10000次模拟,为了随机选择过去的值,我们给它们分配了数字。接着是模拟1-251的随机整数(历史数据的数量),然后使用函数来查找关联的收益率。代码如下:
sim_return <- r[ceiling(runif(10000)*251)]
VaR4 <- -quantile(sim_return, 0.05)
print(VaR4)
5%
0.01578806
这里得出的VAR是1.58%,与历史模拟法得出结果十分接近,意料之中。
如今,风险价值是很多金融领域风险的衡量标准。然而,总的来说,由于它不符合次相加性的标准,它仍然不符合相关风险度量的标准。换句话说,这可能会阻碍某些情况下的多样化。但是,如果我们假设收益率为一个椭圆分布函数,则VAR被证明是一个连贯的风险度量。这基本意味着正态分布很适合估计VAR。唯一的问题是,与高斯曲线相比,现实中的股票回报率相当的尖峰(厚尾)。
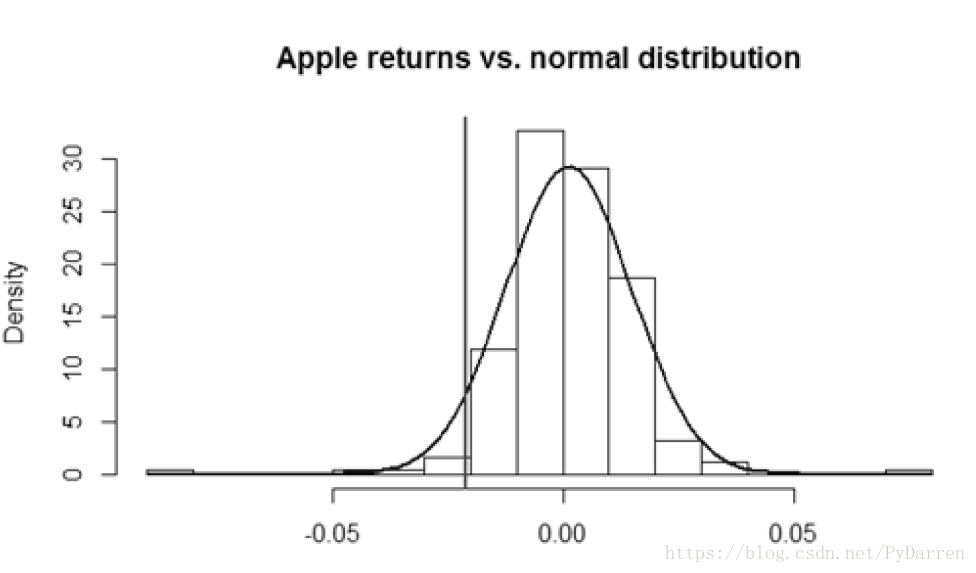
换句话说,现实生活中的股票倾向于表现出比正态分布所解释的更为极端的损失和收益。因此,前沿的风险分析通过假设更复杂的分布来处理厚尾股票收益,异方差和其他现实收益率的不完整性。
预期缺口的使用也包含在已开发的风险分析中,它是一个连贯的风险度量,不论我们假设的分布如何。预期缺口集中在分布的尾部,测量出超出风险价值的分布的预期值。换句话来说,在一个显著水平上的预期缺口是最差α个百分比的期望值。即:
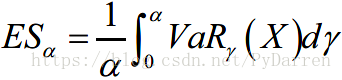
这里的VaRγ是收益率分布的风险价值。
有时,预期缺口被称为条件风险价值(CVAR)。但这两个术语并不是指同一件事情;如果风险分析中用到了连续分布函数的话,两者可为同义词。这些R语言都可以处理。更多内容参考(
Acerbi, C.; Tasche, D. ,2002)。