二分查找
定义
这篇博文主要介绍二分答案和尺取法,不过二分查找是二分答案的基础,所以还要讲一下的。
比如有人跟你玩一个游戏,就是别人想一个\(1000\)以内的数,然后你开始猜答案,对方可以告诉你你猜的大了还是小了,那么你如果尽快的猜出来?
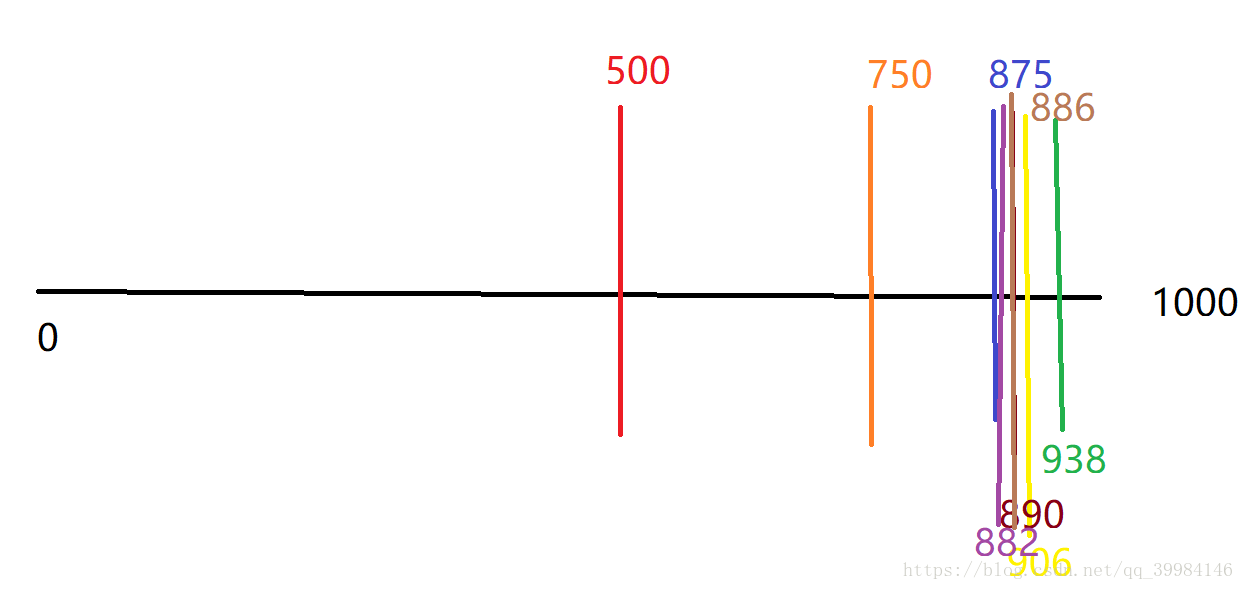
相信有许多人知道,假设对方猜的是\(886\),然后我们开始猜:
我:\(500\)
朋友:小了
我:\(750\)
朋友:小了
我:\(875\)
朋友:小了
我:\(938\)
朋友:大了
我:\(906\)
朋友:大了
我:\(890\)
朋友:大了
我:\(882\)
朋友:小了
我:\(886\)
朋友:对了
这里我们找了\(8\)次,实际上最差情况也就是查找\(10\)次吧。
你可以发现,我们的每一次猜想都可以把问题的规模缩小一半,这就是折半查找,过程图如下(丑):
下面是代码:
#include<iostream>
using namespace std;
int main()
{
int n;
cin>>n;
int l=0,r=1001;
while(l<r)
{
int m=(l+r)>>1;//>>1相当/2
if(m<n) l=m;//二分要注意边界的问题
else r=m;
cout<<m<<endl;
if(m==n) return 0;
}
return 0;
}不过要注意的一点是,我们查找的\(1000\)以内的数,当你输入的\(n\)在\(1000\)以外了那么就会查找不到,可以通过扩大右端点的范围来解决。
你可能想:既然知道了数,为什么要那么费时费力的去找?实际上很多时候你都是布吉岛这个数的,你需要找到这个数,通过二分查找可以将复杂度变为\(log\)级的。
例子还是算了吧\(QAQ\)。
二分答案
定义
顾名思义,下面是一个帮助理解的图片
二分答案可以在已知数据范围并且有单调性的情况下可以使用,最常见的是: “最大值最小化” 或者 “最小值最大化”。
模板给大家一下,来自:Link
求最小值
int binary()
{
int l = 0, r = ll, mid;
while(l < r)
{
mid = (l + r) >> 1;
if(check(mid)) r = mid; //大多数题只要改改check()即可
else l = mid + 1;
}
return l;
}求最大值
int binary()
{
int l = 0, r = ll, mid;
while(l < r)
{
mid = (l + r + 1) >> 1;
if(check(mid)) r = mid - 1;
else l = mid;
}
return l;
}例题
然后我们一起做一道经典的题目:
中文就不给翻译了。
思路
看到这道的数据范围题我们可以考虑用可持久化线段树维护一些啥的。
正解之一是两个二分,复杂度几乎是\(O(nlogn)\)。
这题按照套路先考虑求这些数里多少个数大于\(x\),很简单的,直接枚举会很慢,于是采用二分(复杂度主要在这里,可以通过下面讲的尺取法来降低复杂度)。
那么我们的目的是找到一个\(x\),大于\(x\)的数\(==k\),按照模板套二分即可,我没有写二分答案的\(check\),下面的代码来自一个和我的代码风格比较像的人的博客:Link。
Code
#include<cstdio>
#include<cstring>
#include<algorithm>
using std::sort;
const int N=50010;
#define ll long long
ll a[N],b[N];
int n,k;
inline ll check(ll x)
{
int sum=0;
for(int i=1;i<=n;i++)
{
int l=1,r=n;
ll ans,mid;
while(l<r)
{
mid=(l+r)>>1;
ans=a[i]*b[mid];
if(ans>x) r=mid;
else l=mid+1;
}
ans=a[i]*b[l];
if(ans>x) sum+=(n-l+1);
else
{
ans=a[i]*b[r];
if(ans>x) sum+=(n-r+1);
}
}
return sum;
}
int main()
{
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++) scanf("%lld %lld",&a[i],&b[i]);
sort(a+1,a+1+n),sort(b+1,b+1+n);
ll l=a[1]*b[1],r=a[n]*b[n];
ll ans=0,mid;
while(r>l)
{
mid=(l+r)>>1;
ans=check(mid);
if(ans>k-1) l=mid+1;
else r=mid;
}
if(check(l)>k-1) printf("%lld\n",l);
else printf("%lld\n",r);
return 0;
}尺取法
定义
尺取法,我更愿意叫它为两个指针,应用于有这么一类问题,需要在给的一组具有单调性的数据中找到不大于某一个上限的最优连续子序列。
尺取法:顾名思义,像尺子一样取一段,借用挑战书上面的话说,尺取法通常是对数组保存一对下标,即所选取的区间的左右端点,然后根据实际情况不断地推进区间左右端点以得出答案。之所以需要掌握这个技巧,是因为尺取法比直接暴力枚举区间效率高很多,尤其是数据量大的.
例题
还是刚才那一道题。。
思路
当数据范围是\(2 \leq N \leq 50000\),上面的做法是可以的,不过当数据达到了\(1000000\)或者更大的话,上面的做法就不是很可取了(别忘了二分答案还有复杂度)。这个时候就需要减少有多少个数大于\(x\)了,这里复杂度是\(O(n)\)(由于排序,所以总体复杂的)。
那么让我们找一下这道题的单调性,别忘了你把这些数排序了,也就是说,假如你\(a_n*b_{1......c} \leq x\),那么在\(a_{n-k}*b_{1......d} \leq x\)的情况下,一定满足\(d \leq c\)的。
于是用尺取法来做这道题效率更高。
Code
//复杂度几乎是O(n)
#include <cstdio>
#include <iostream>
using namespace std;
const int maxx=5e4+6;
ll a[maxx],b[maxx];
int n,k;
bool check(long long x)//尺取法
{
int j=n-1,sum=0;
long long temp;
for(int i=0;i<n;i++)
{
while(a[i]*b[j]>x) bj--;
sum+=n-j-1;
}
return sum<k;
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=0;i<n;i++)
scanf("%d%d",&a[i],&b[i])
sort(a,a+n);
sort(b,b+n);
long long left=a[0]*b[0],right=a[n-1]*b[n-1],mid;
while(left<right)//二分答案
{
mid=(left+right)>>1;
if(judge(mid)) right=mid;
else left=mid+1;
}
cout<<left<<endl;
return 0;
}