红黑树是AVL树的另一变种,他也能在动态变化的过程中保持某种意义的平衡,对红黑树的操作最坏情况下也只有$O\left( \log n \right)$的复杂度,而且下面我们会看到,对于插入而言我们有另外一种比AVL树更容易的实现方法,非递归的。在具体谈到技术细节之前,我们或许会有疑问:已经有AVL这种渐进复杂度很低的结构了,也能保持平衡,不至于让树高突破天际,那为什么还要研发新的变种呢?动力何在,红黑树在整个平衡树体系里又处于什么地位呢?先看下今天主角的基本信息。
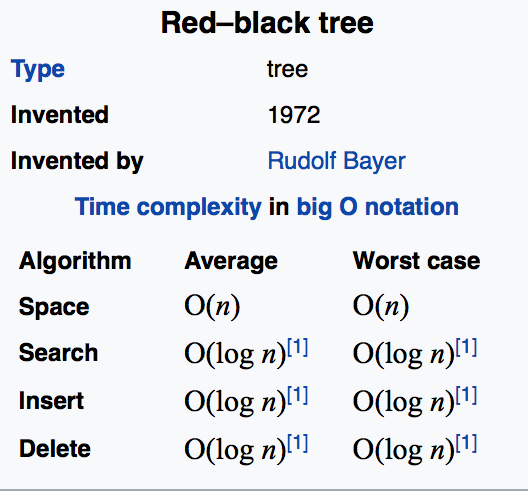
回顾此前的各个结构,不论是线性的向量、列表、栈or队列,也无论半线性的树结构和非线性的图。它们大多呈现这种特征:每经一次动态的操作,逻辑结构变化,然后转入新的状态,此前的状态完全丢失,这类结构也因此称作ephemeral data structure。每一个固定时刻的状态都是稍纵即逝的。但是实际场景中这并不够用,很多时候我们可能希望查阅它的历史版本并加以修改之类的。那此前所学就不足以解决问题了,因此要设计新的结构,这是它的动力所在。因此无论静态还是动态操作,除了元素的值,还需要同时指定一个版本号。如果一个数据结构能够支持这种类型的需求,就称作是persistent structures,也就是所谓的一致性结构,或者叫可持久化结构(这里给个拓展阅读,陈立杰写过一篇论文叫《可持久化数据结构研究》,对这方面有兴趣的可以研读一番)。乍看之下很好实现这个思想:每做一次动态操作就复制一份副本就行了,每个版本独立保存。但这种朴素(如同村中老汉一般)的想法行得通么?以下就是针对一棵具体的平衡二叉树记录了它整个生命期内的5个版本:

如此一来,一旦指定了版本号就可以转入对应的状态,从单次访问效率而言,这个结构还可以接受。如果我们将不同版本的数目记作h,就需要$O\left( \log h \right)$时间确定状态,然后用$O\left( \log n \right)$时间执行操作,总体来说单次操作$O\left( \log h\; +\; \log n \right)$,时间复杂度海星。但是空间复杂度就爆炸了,每一个元素都可能会被保存多份,渐近的来说n个元素中的每一个,都有可能在这组档案中被保存多达h份。这就意味着空间复杂度将伴随着h成线性的速度增长,而空间复杂度也构成了时间复杂度的一个下限。刚才单次的渐进时间是log级别的,现在累计花费的时间会达到$O\left( h\; +\; n \right)$的规模,这肯定不行。那能不能做点改进呢?控制在$O\left( n\; +\; h\; \cdot \; \log n \right)$内:除了所有元素各自占用的空间,能够将每一个版本所消耗的均摊空间量控制在$\log n$的范围内呢?
答案是可以
为此我们需要利用同一数据结构相邻版本之间的关联性。对于每一组相邻的版本,新版本都是在老版本上做些许修改得到的:

两个版本绝大部分元素是相同的,二者差异不大。利用这个特点我们很自然的想到一个办法:大量共享,少量更新(就类似前缀和的区间加,大部分不变,做少量修改)。只要实现得当,就能把动态操作的复杂度控制在$O\left( h\; +\; n \right)$。比如对于具体的一棵树,下面是一种可行的实现方法。

在这幅图中每一条红线都对应于一个共享,比如1-2这条红线,表示节点1同时出现在版本0和1中。其中还有一些蓝色的虚线,它们表示在相邻版本之间的更新量,也是我们必须花费空间存储的量。好消息是:这个量不会太大。比如左边第一条8-8'的蓝线就表示:尽管8和8'对应于同一个数据对象,但是在前和后两个版本中它们的父节点已经发生了变化,因此在新的版本中我们必须为它另存一个副本。听起来有点绕,的确,这种高级结构已经牵扯到计算几何的范畴了。另外$\log n$其实还有改进空间,如果能将前后版本的空间差异控制在$O\left( 1 \right)\; $的范围,那么整体的空间复杂度将进一步优化至$n\; +\; h$ 而不是$h\; \cdot \; \log n$。这也是可以做到的。
具体细节先不说,但是为此所应具备的一项必要条件是非常好理解的:对BBST的树形拓扑结构而言,相邻版本之间的差异不能超过常数。令人遗憾,绝大多数的BBST,包括此前学过的AVL树都不能保证这一点。拓扑结构差异是由自调整过程中的旋转操作导致的,每一次局部的旋转 ,都意味着在结构上引入差异。反过来说,如果需要保证前后版本在拓扑结构上的差异不超过常数,就必须保证:2个版本之间的旋转操作不得超过一个固定数值,这个数不能因输入量而变。
满足这个优化条件的结构在已学的知识里有么?来找一找,AVL树的两个动态操作中插入是满足的。每次插入之后,一次旋转,全树复原。但是删除就不满足这个了,从AVL树中删除一个节点之后,有可能自底而上逐层引发多达$\log n$次的旋转,从而导致树形拓扑结构的剧烈变化。因此为了使得上述的构思能够兑现,我们就需要这样一种BBST,它的任何动态操作对树形拓扑结构的影响,都能控制在常数的范围之内。发明这个变种之后,根据特征我们将其命名为“红黑树”。
阶段性总结一下:红黑树相比于AVL树的特点在于,每次插入/删除后拓扑结构的变化不超过$O\left( 1 \right)\; $。
现在来分析一下RBTree的结构。
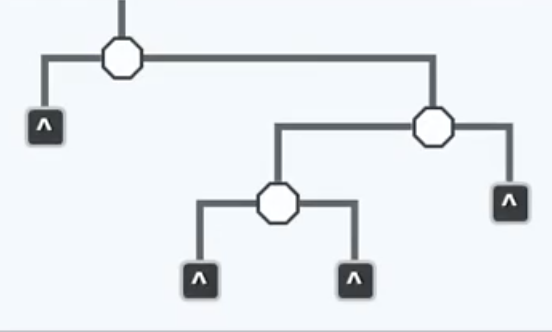
增设外部节点nULL,方便考虑,就相当于left=right=nULL的初始情况,这时候这些外部节点就是叶子了。对于这种树有如下四条定义统一约束:
- 树根是黑色的,叶子(即使是nULL)也是黑色的
- 除了root和leaf,每一个节点或红或黑
- 如果一个节点是红色的,那子节点必须是黑色
- 从某个节点到叶子的路径上必须包含相同数目的黑色节点
挑几个说明一下,第3条虽然简明,但实际上蕴含了很多人生的经验性质,比如这要求了不可能出现同时为红的父子两代,换一个有可操作性的表述就是:对于红节点来说,无论是它的孩子还是父亲都必须是黑的,就是可以红黑相间or全黑(它只约束了红色嘛),不准全红。待会我们就会看到,这条规则对于控制红黑树的深度是极其重要的。第4条,可以认为是旨在控制红黑树的平衡性。因为这里要求了,在从任何一个外部节点通往树根的唯一的路径上,黑节点的数目必然相等,那肯定是平衡的,不会一边长一边短。
那这一堆规则到底对应一棵什么样的树?而这些规则背后又有着什么原理呢?我们来看一个例子:

根是黑色的,叶子貌似不是,但实际上我们之前增加了外部节点,这时候令外部节点统一为黑即可。增设这些是为了方便分析和实现,在例子中我们可以忽略掉。第三条也是满足的,每一个红色节点的父与子都是黑色的。第四点也是满足的,找两条路径数一下就好了。现在有了一些直观感受,但是,回过头去看那四条规则仍感觉艰深晦涩(e.g 凭啥两个红色节点不能挨着、我两条路径上黑色节点数量不一样能咋地?)。那还能不能再直接一点呢?
他山之石,可以攻玉,我们要用另外一个结构帮助理解。我们来看下面这个案例,为了更好地理解这组规则,我们要做一个等价变换:提升。先看下图:
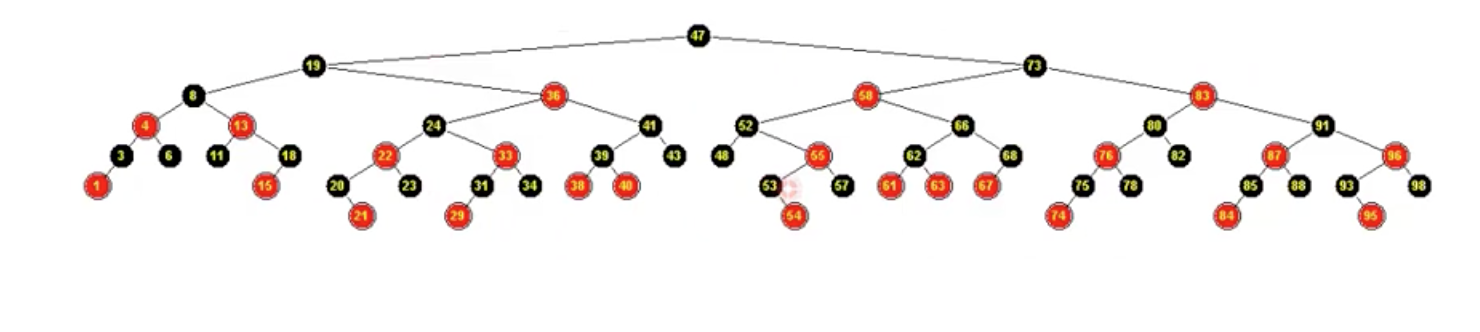
我们把每一个红色节点都往上提一层,让他和黑色的父亲同高(注意,部分黑色节点可能会接纳两个红节点)。可以证明的是,绝对不可能出现两个红色节点相邻的情况,不可能。就算在一行上,他们之间必然夹着一个黑色节点。现在开始吧——超级变换形态

变成这样了。再来看一个更大的例子,方便我们从宏观上把握红黑树的性质。

这是一颗100个节点的树,底层节点都是red,而且凹凸不平(这对控制树高十分不利)。变换之后呢?来玩个找不同游戏:所有底层节点都同高了,对吧!那这一现象是巧合么?

尽管红黑树的规则艰深晦涩,玄之又玄,但是从提升变换的角度来看,就会变得豁然开朗,宛如一幅长卷铺开。实际上从这个角度来看,红黑树就是4阶的B树,(2,4)树。实际的确如此,为了理解这点,只需要将每一个黑节点,与经过提升之后与它高度一致的红节点,整体地视作为一个B树的内部节点。这样一来,归纳下来不过四种组合,每一种黑父与红子的组合都对应4阶B树的某类内部节点:
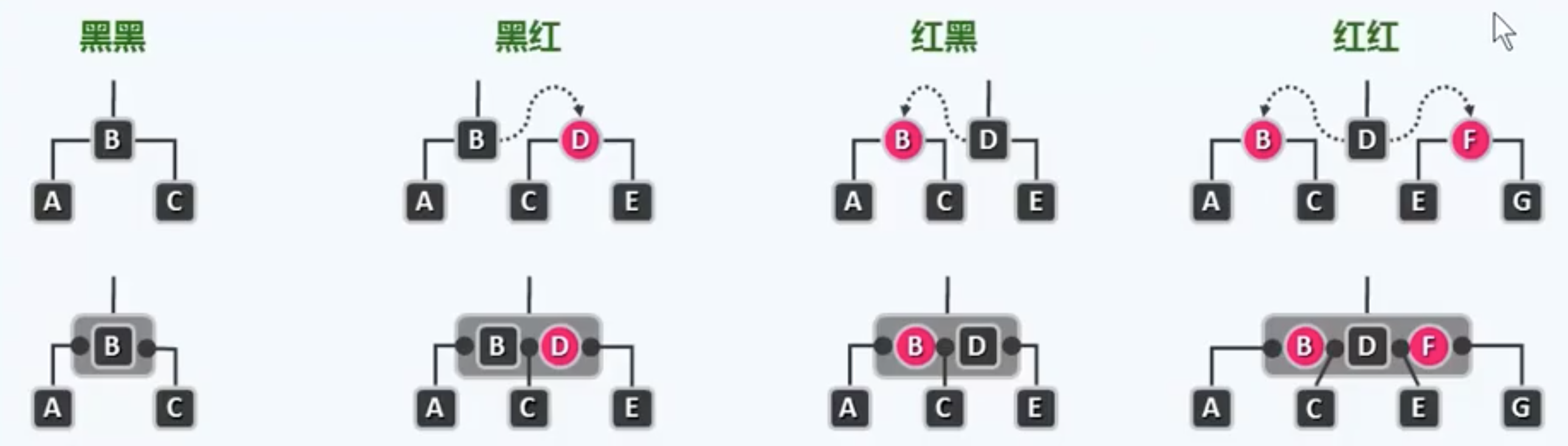
每一个内部节点都至少拥有2个分支,至多拥有4个分支,正是4阶B树的特征。
那他既然也是B树,自然也是平衡树,我们来个证明吧,这是十分有必要的,因为这会加深对他的理解。我们需要证明的是:由n个内部节点所构成的任何一棵红黑树,其高度在渐近意义下都不超过logn,当然与所有的BST一样——拥有n个内部节点的红黑树,也必然同时拥有n+1个外部节点。简单点说就是证明$\log _{2}\left( n\; +\; 1 \right)\; \leq \; h\; \leq \; 2\; \cdot \; \log _{2}\left( n\; +\; 1 \right)$这个不等式成立。左边的在B-树篇已经证明了,而且任何BST都是满足的,所以现在只证右边的的就好了。
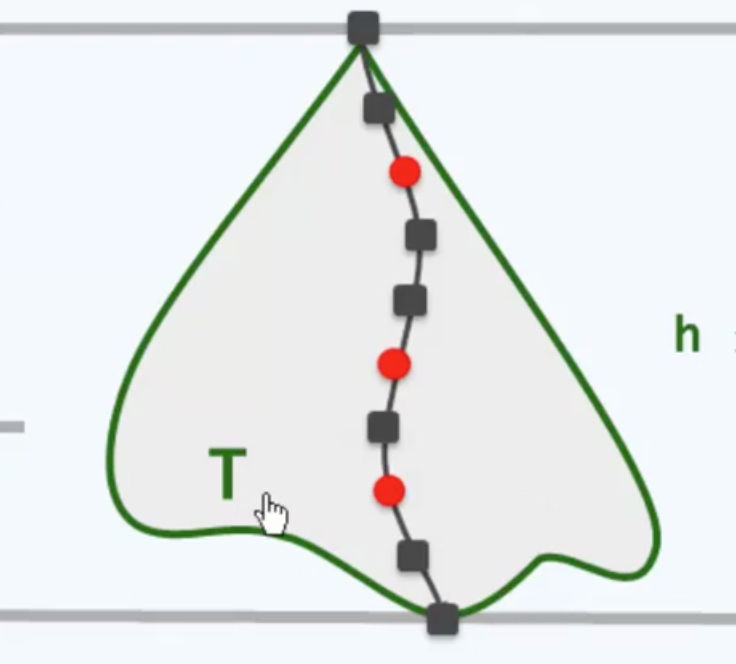
比如就在这棵红黑树中,如果忽略掉人为引入的外部节点,那么每一条这样的路径上所含黑节点是6个。根据规则任何一条路径上所含黑节点的总数都应该是6,此时我们就称这棵红黑树的黑高度为6。尽管加上3个红色节点,高度可以到9。所谓树高就是全树中最深节点所对应那条通路的长度,而在红黑树中任何一条通路上,可能出现相邻的黑节点,却不允许出现相邻的红色节点。这就意味着在每一条这样的通路上,红色节点$\leq \; \frac{1}{2}$,而黑色节点$\geq \; \frac{1}{2}$。因此红黑树的高度必然不会超过其黑高度的2倍。
那么这里的黑高度又如何计算呢?正是提升变换。我们知道经过提升变换之后,红黑树对应于4阶的B树
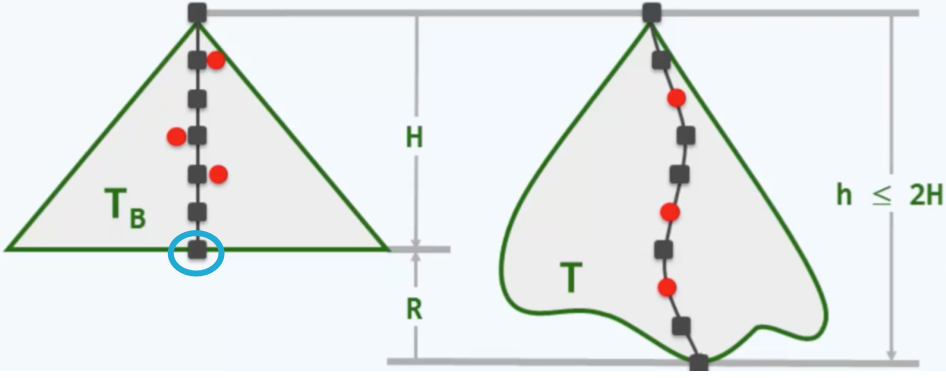
在这样一棵B树中所有的外部节点都像蓝圈中的一样,整齐的分布于底层。而其中的每一个内部节点都是由此前的某个黑父以及他的红子构成的,因此此前红黑树中的每一条路径
也会在B树中对应于一条路径。原先这条路径上有多少个黑节点,在B树中对应的那条路径就有多长——这就意味着,这棵B树的高度应该正好是此前那棵红黑树的黑高度。也就是:B树的高度就是其对应的红黑树的黑高度。而为了计算一棵红黑树的黑高度,只需去计算对应的B树高度即可。也就是$h\; \leq \; \log _{2}\frac{n+1}{2}\; +\; 1\; \leq \; \log _{2}\left( n\; +\; 1 \right)$
下篇写实现