矩形区域处理
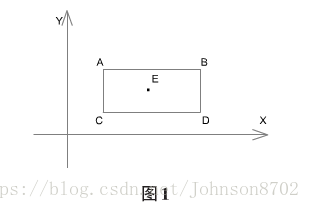
针对矩形区域处理,复杂度较低。设矩形ABCD的四个顶点分别为A、B、C、D,坐标分别为A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),设点E(x5,y5)是需要判断的点。那么判断点E是否在矩形区域的方法是:x5>x3且x5<x2,同时满足y5>y3且y5<y2,当然我们也可以把A、D两个点作为参照
/**
* 判断是否在矩形范围内
* @param lat 测试点纬度
* @param lng 测试点经度
* @param minLat 纬度范围限制1
* @param maxLat 纬度范围限制2
* @param minLng 经度范围限制1
* @param maxLng 经度范围限制2
* @return
*/
public static boolean isInRectangleArea(double lat, double lng, double minLat, double maxLat, double minLng, double maxLng){
if(isInRange(lat, minLat, maxLat)){//如果在维度范围内
if(minLng*maxLng>0){
if(isInRange(lng, minLng, maxLng)){
return true;
}else{
return false;
}
}else{
if(Math.abs(minLng)+Math.abs(maxLng)<180){
if(isInRange(lng, minLng, maxLng)){
return true;
}else{
return false;
}
}else{
double left = Math.max(minLng, maxLng);
double right = Math.min(minLng, maxLng);
if(isInRange(lng, left, 180) || isInRange(lng, right, -180)){
return true;
}else{
return false;
}
}
}
}else{
return false;
}
}
圆形区域处理
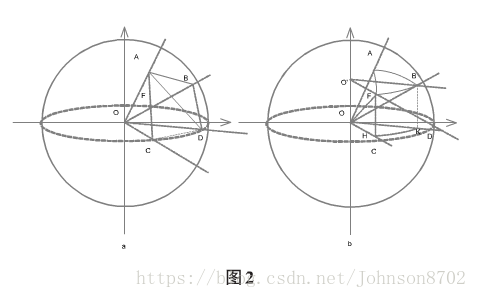
对于圆形区域,我们假设地球是正圆的,同时假设圆心为B(Xb,Yb),A(Xa,Ya)为判断的点,Xb,Yb为B点经纬度,Xa,Ya为A点经纬度,A,B是地球表面的两个点,如图2中的a所示,已知A、B两点的经度后,我们可以计算CD的地面长度为:
,R地球半径 (1)
将CD向上平移至FB,F、G、B、A在球面上,沿着O'O的方向投影,如图2中的b,FB在面OCD的投影为HK,HK的长度和FB长度相等,即
(2)
由式(1)和式(2)知:
(3)
AF的长度为:
(4)
AF是垂直于FB,不考虑地表曲面,满足
(5)
因为B为圆心,A在圆内的条件是AB长度小于圆的半径r,根据式(1)、式(3)、式(4)、式(5)知:
(6)
CD不但可以平移至B点,也可以 平移至A点,当然算出的结果不一样,这里将式(6)中的Yb取值为(Ya+Yb)/2,即去平均值,效果较佳。
/**
* 地球半径
*/
private static double EARTH_RADIUS = 6378138.0;
private static double rad(double d){
return d * Math.PI / 180.0;
}
/**
* 计算是否在圆上(单位/千米)
* @param radius 半径
* @param lat1 维度
* @param lng1 经度
* @return
*/
public static boolean isInCircle(double radius, double lat1, double lng1, double lat2, double lng2){
double radLat1 = rad(lat1);
double radLat2 = rad(lat2);
double a = radLat1 - radLat2;
double b = rad(lng1) - rad(lng2);
double s = 2 * Math.asin(Math.sqrt(Math.pow(
Math.sin(a/2), 2) +
Math.cos(radLat1)*Math.cos(radLat2)*Math.pow(Math.sin(b/2), 2)));
s = s * EARTH_RADIUS;
s = Math.round(s * 10000) / 10000;
if(s > radius){//不在圆上
return false;
}else{
return true;
}
}多边形区域处理
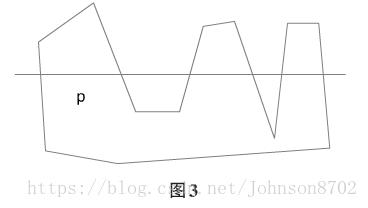
如图3,判断点p在多边形内的方法是:用点p的水平坐标去和多边形相交,得到若干个交点,如果点p两侧的交点数量都是奇数个时,说明p点在多边形内,即铅垂线内点法。使用这种方法,适合任意多边形,包括凸多边形和凹多边形,同时适用于有孔的多边形。下面给出这种算法的Java实现
/**
* 判断点是否在多边形内
* @param polygon 多边形
* @param point 检测点
* @return 点在多边形内返回true,否则返回false
*/
public static boolean IsPtInPoly(List<Point2D.Double> polygon, Point2D.Double point){
int N = polygon.size();
boolean boundOrVertex = true;//如果点位于多边形的顶点或边上,也算做点在多边形内,直接返回true
int intersectCount = 0;//cross points count of x--交叉点计数X
double precision = 2e-10;//浮点类型计算时候与0比较时候的容差
Point2D.Double p1, p2;//neighbour bound vertices--临近绑定顶点
Point2D.Double p = point;//当前点
p1 = polygon.get(0);//left vertex--左顶点
for (int i = 1; i <= N; ++i) {//check all rays--检查所有射线
if(p.equals(p1))
return boundOrVertex;//p is an vertex--p是一个顶点
p2 = polygon.get(i % N);//right vertex--右顶点
if(p.x < Math.min(p1.x, p2.x) || p.x > Math.max(p1.x, p2.x)){//ray is outside of our interests--射线不在我们的兴趣范围之内
p1 = p2;
continue;//next ray left point--下一条射线的左边点
}
if(p.x > Math.min(p1.x, p2.x) && p.x < Math.max(p1.x, p2.x)){//ray is crossing over by the algorithm(common part of)--射线被算法穿越(常见的一部分)
if(p.y <= Math.max(p1.y, p2.y)){//x is before of ray--x在射线之前
if(p1.x == p2.x && p.y >= Math.min(p1.y, p2.y)){//overlies on a horizontal ray--在一条水平射线上
return boundOrVertex;
}
if(p1.y == p2.y){//ray is vertical--射线是垂直的
if(p1.y == p.y){//overlies on a vertical ray--覆盖在垂直光线上
return boundOrVertex;
}else{//before ray--射线之前
++intersectCount;
}
}else{//cross point on the left side--左边的交叉点
double xinters = (p.x - p1.x) * (p2.y - p1.y) / (p2.x - p1.x) + p1.y;//cross point of y--y的交叉点
if(Math.abs(p.y - xinters) < precision){//overlies on a ray--覆盖在射线
return boundOrVertex;
}
if(p.y < xinters){//before ray--射线之前
++intersectCount;
}
}
}
}else{//special case when ray is crossing through the vertex--特殊情况下,当射线穿过顶点
if(p.x == p2.x && p.y <= p2.y){//p crossing over p2--p交叉p2
Point2D.Double p3 = polygon.get((i+1) % N);//next vertex--下一个顶点
if(p.x >= Math.min(p1.x, p3.x) && p.x <=Math.max(p1.x, p3.x)){//p.x lies between p1.x & p3.x--p.x在p1.x和p3.x之间
++intersectCount;
}else{
intersectCount += 2;
}
}
}
p1 = p2;//next ray left point--下一条射线的左边点
}
if(intersectCount % 2 == 0){//偶数在多边形外
return false;
}else{//奇数在多边形内
return true;
}
}