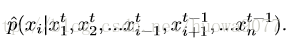问题来源:
论文 Shape and Material from Sound NIPS 2017
4.Inference 中 4.1 Models
Unsupervised Given an audio clip S, we would like to recover the latent variables x to make the reproduced sound g(x) most similar to S. Let L(·,·) be a likelihood function that measures the perceptual distance between two sounds, then our goal is to maximize L(g(x),S). We denote L(g(x),S) as p(x) for brevity. In order to find x that maximizes p(x), p(x) can be treated as an distribution pˆ(x) scaled by an unknown partition function Z. Since we do not have an exact form for p(·), nor pˆ(x), we apply Gibbs sampling to draw samples from p(x). Specifically, at sweep round t, we update each variable xi by drawing samples from
Such conditional probabilities are straightforward to approximate. For example, to sample Young's modulus conditioned on other variables, we can use the spectrogram as a feature and measure the l2 distance between the spectrograms of two sounds, because Young's modulus will only affect the frequency at each collision. Indeed, we can use the spectrogram as features for all variables except height. Since the height can be inferred from the time of the first collision, a simple likelihood function can be designed as measuring the time difference between the first impact in two sounds. Note that this is only an approximate measure: object's shape and orientation also affect, although only slightly, the time of first impact.
贝叶斯网络(Baysian Network)是统计推断中的重要工具。简单地说,贝叶斯网就是对于由一系列待估计量作为自变量的联合分布的一种描述。即贝叶斯网描述了如下的后验分布,其中代表一个待估计变量构成的向量,为一系列的已知测量量。原则上讲,如果我们能够写出的具体表达式,我们就能给出关于的统计特征的描述,从而直接求解这一统计推断问题。如果必要,在贝叶斯的框架下,我们可以将这一后验概率进一步展开为
即先验概率和似然函数的乘积。如果我们有后验概率的具体表达式,原则上我们可以对待估计变量的统计特征进行直接估计。然而现实并不那么美好,如果的维度很高,而且后验概率形式特别复杂,往往导致在对的某个分量求解边缘分布时的积分无法简单直接求得。例如,求某个分量的期望就必然涉及对后验概率的积分。蒙特卡罗积分法对于高维度的积分问题而言是一种可行的解决方案,基于这一原理,我们就能用基于抽样的方法来解决这一问题(这里的抽样是指按照给定的联合分布产生一个符合该分布的样本,而不是指从一个总体中抽取出一个样本)。
如果我们能够对后验概率进行采样,即根据后验概率获得一系列 的实现样本,我们就能够对这个样本进行直接的统计,从而获得对的估计。那么如何完成对的采样呢?这时候我们便要请出吉布斯(Gibbs)采样算法了。吉布斯采样算法是一种对多元分布进行采样的算法。吉布斯采样算法的基本思想很直接,就是依次对的各个分量进行采样,在采样某一个分量的时候,认为其他分量固定。这就将多维采样问题转换为了对一维分布进行采样,而这能够用拒绝算法(或者自适应拒绝算法)、切片法等等解决。本来故事到这里已经可以结束,从而没有贝叶斯网什么事情了,但是实践中,我发现(当然不可能是我首先发现的),直接对后验概率进行吉布斯采样,虽然能凑合着用,但是效率有时候堪忧,贝叶斯网的出现可以显著改善采样的效率。如果我们能够把后验概率进行分解, 把各个参量之间的关系捋顺,在对某一具体分量进行采集的时候,只需要计算和它相关的量,就能大大降低计算复杂性,从而提高效率。
算法(机器学习:p334):
假定x={x1,x2......xn},目标分布为p(x),在初始化x的初值后,通过循环执行以下步骤来完成采样:
(1)随机或以某个次序选取变量xi
(2)根据x中除xi外的变量的现有取值,计算条件概率p(xi|xi-),其中xi-={x1,x2,x3.....xi-1,xi,xi+1,....xn}
(3)根据p(xi|xi-)对变量xi采样,用采样值代替原值
算法(机器学习:p161)
令Q={Q1,Q2....Qn},表示待查询变量E={E1,E2,...Ek}为证据变量,已知其取值为e={e1,e2,...ek},目标是计算后验概率P(Q=q|E=e),其中q={q1,q2,....qn}是待查询变量的一组取值,以西瓜问题为例,待查询变量为Q={好瓜,甜度},证据变量为E={色泽,敲声,根蒂},且已知其取值为e={青绿,浊响,蜷缩},查询的目标值是q={是,高},即这是好瓜且甜度高的概率有多大。
吉布斯采样算法先随机产生一个与证据E=e一致的样本q0作为初始点,然后每步从当前样本出发,产生下一个样本,具体来说,在第t次采样中,算法先假设qt=qt-1,然后对非证据变量逐个采样改变其取值,采样概率根据贝叶斯网B和其他变量的当前取值(即Z=z)计算获得,假设经过T次采样得到的与q一致的样本共有nq个,则可近似估算出后验概率
P(Q=q|E=e)~—nq/T
参考:<机器学习> 周志华
https://zhuanlan.zhihu.com/p/20753438