https://www.nowcoder.com/acm/contest/81/F
循环卷积的裸题,太久没做FFT了,这么裸的循环卷积都看不出来
注意一下的mod 都是指表示幂的模数,而不是NTT用到的模数
- 首先我们先不管m,考虑多项式
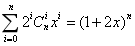
可以发现这个是一个多项式的n次幂,正常求一个多项式的n次幂,可以用快速幂套NTT,复杂度n*log(n)*log(n), 最多只能做n在1e4左右的题。
- 现在在来考虑m,则原式为。
 显然这就是循环卷积的常见形式
显然这就是循环卷积的常见形式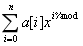
如果先用快速幂套NTT 把多项式系数算出来a[i], 再对i%mod同余的系数进行累加,时间和空间都是会爆炸的。
不过在多项式快速幂实现的时候可以发现,可以每做一次多项式乘法,就对幂取余一次,合并幂的余数相同的项。这样空间可以降到2*mod, 时间复杂度 mod*log(mod)*log(n) 但是这样还是会超时的
- 最后重点来了,上面是一般的情况的下循环卷积的做法,循环卷积还有一种特殊情况,就是指数的mod=2^m 时,这时循环卷积可以直接变成频域上的2^m-1 次多项式的点乘(注意要系数等于2^m-1 的点乘, 不需要先以前一样开两倍大小,以防止多项式系数溢出,这里就是要溢出才能保证正确性),这时可以发现,NTT 前可NTT后都是mod-1次多项,没有系数合并的那一步,所以干脆中间乘的时候,就不要NTT回来, 直接在点成的时候做快速幂。 这样只需做一次NTT和逆NTT.时间复杂度 mod*(log(n)+log(mod))

#include<stdio.h> #include<string.h> #include<algorithm> using namespace std; typedef long long ll; #define N 2000005 ll a[N],b[N]; const ll PMOD=998244353; const ll PR=3; static ll qp[30]; ll res[N]; struct NTT__container { NTT__container() { int t,i; for( i=0; i<21; i++)///注意循环上界与2n次幂上界相同 { t=1<<i; qp[i]=quick_pow(PR,(PMOD-1)/t); } } ll quick_pow(ll x,ll n) { ll ans=1; while(n) { if(n&1) ans=ans*x%PMOD; x=x*x%PMOD; n>>=1; } return ans; } int get_len(int n)///计算刚好比n大的2的N次幂 { int i,len; for(i=(1<<30); i; i>>=1) { if(n&i) { len=(i<<2); break; } } return len; } inline void NTT(ll F[],int len,int type) { int id=0,h,j,k,t,i; ll E,u,v; for(i=0,t=0; i<len; i++)///逆位置换 { if(i>t) swap(F[i],F[t]); for(j=(len>>1); (t^=j)<j; j>>=1); } for( h=2; h<=len; h<<=1)///层数 { id++; for( j=0; j<len; j+=h)///遍历这层上的结点 { E=1;///旋转因子 for(int k=j; k<j+h/2; k++)///遍历结点上的前半序列 { u=F[k];///A[0] v=(E*F[k+h/2])%PMOD;///w*A[1] ///对偶计算 F[k]=(u+v)%PMOD; F[k+h/2]=((u-v)%PMOD+PMOD)%PMOD; ///迭代旋转因子 E=(E*qp[id])%PMOD;///qp[id]是2^i等分因子 } } } if(type==-1) { int i; ll inv; for(i=1; i<len/2; i++)///转置,因为逆变换时大家互乘了对立点的因子 swap(F[i],F[len-i]); inv=quick_pow(len,PMOD-2);///乘逆元还原 for( i=0; i<len; i++) F[i]=(F[i]%PMOD*inv)%PMOD; } } inline void inv(ll *a,int len)///答案存在res中 { if(len==1) { res[0]=quick_pow(a[0],PMOD-2); return ; } inv(a,len>>1);///递归 static ll temp[N]; memcpy(temp,a,sizeof(ll)*(len>>1)); NTT(temp,len,1); NTT(res,len,1); int i; for(i=0; i<len; i++) res[i]=res[i]*(2-temp[i]*res[i]%PMOD+PMOD)%PMOD;///多项式逆元迭代公式 NTT(res,len,-1); memset(res+(len>>1),0,sizeof(ll)*(len>>1)); } void mul(ll x[],ll y[],int len)///答案存在x中 { int i; NTT(x,len,1);///先变换到点值式 NTT(y,len,1);///先变换到点值式上 for(i=0; i<len; i++) x[i]=(x[i]*y[i])%PMOD;///在点值上点积 NTT(x,len,-1);///再逆变换回系数式 } } cal; void print(ll a[],int len) { int high=0,i; for(i=len-1; i>=0; i--) { if(a[i]) { high=i; break; } } for(i=high; i>=0; i--)putchar(a[i]+'0'); puts(""); } int main() { int m,i,j,k,len; long long n; // printf("%lld\n",PMOD); scanf("%lld%d",&n,&m); len=1<<m; a[0]=1; a[1]=2; cal.NTT(a,len,1); for(i=0;i<len;i++) { a[i]=cal.quick_pow(a[i],n); } cal.NTT(a,len,-1); long long temp=1,ans=0; for(i=0;i<len;i++) { ans+=temp*a[i]%PMOD; temp=temp*2222303%PMOD; } printf("%lld\n",ans%PMOD); return 0; }
