目录
1.关于均匀分布
在概率论和统计学中,均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义,它们是数轴上的最小值和最大值,通常缩写为U(a,b)。
举个栗子,掷骰子就是一个均匀分布,概率论中一个很常用分布。
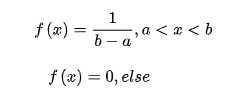
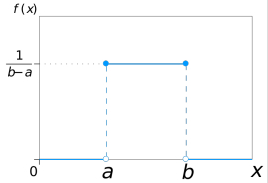
%% 利用rand函数产生服从(a-b)均匀分布的随机序列。
clear
close all
a=2; % (a-b)均匀分布下限
b=3; % (a-b)均匀分布上限
fs=1e7; % 采样率,单位:Hz
t=1e-3; % 随机序列长度,单位:s
n=t*fs;
rand('state',0) ;% 把均匀分布伪随机发生器置为0状态
u=rand(1,n); % 产生(0-1)单位均匀信号
x=(b-a)*u+a; % 广义均匀分布与单位均匀分布之间的关系
subplot(211);plot(x); % 输出信号图
title('均匀分布信号');
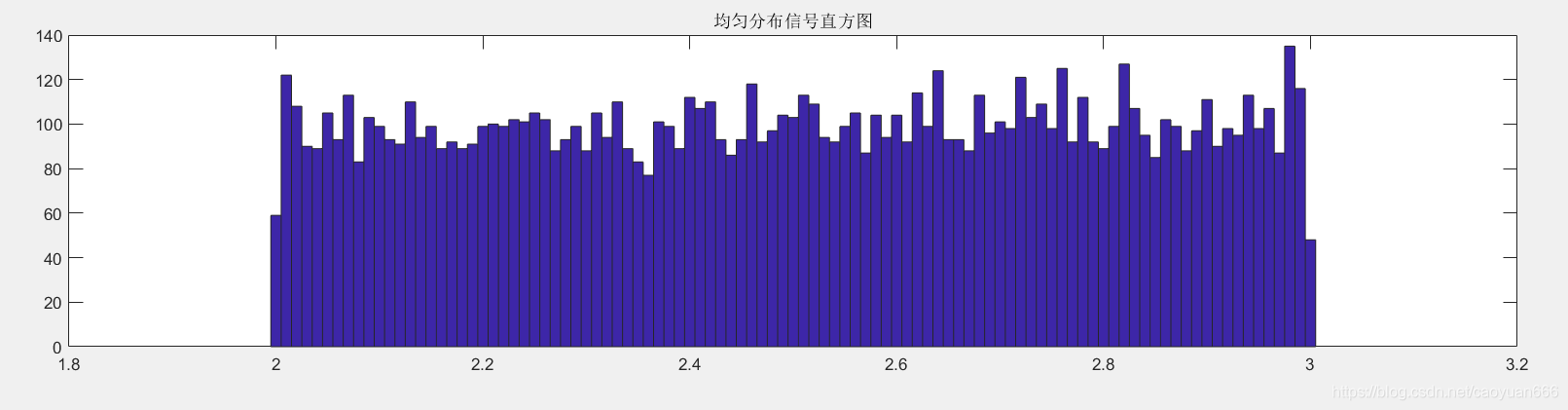
subplot(212);hist(x,2:0.01:3); % 输出信号的直方图
title('均匀分布信号直方图');
2、高斯分布(正态分布)
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
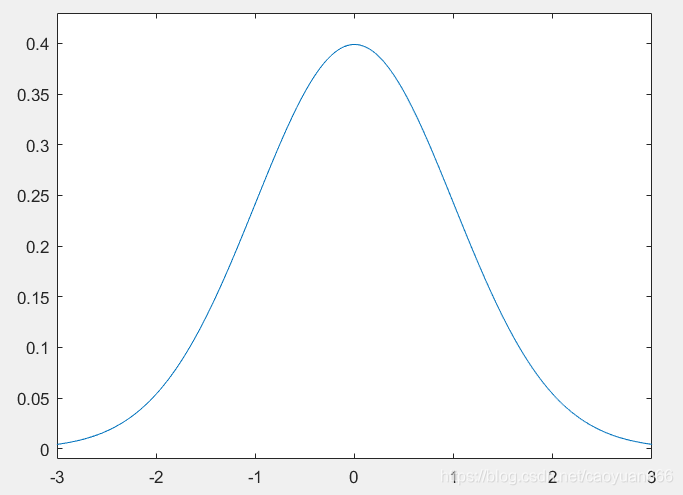
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
生活中很多现象均近似符合整体分布,如整个班级同学的身高、体重情况。
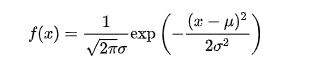
%%正态分布
x=-10:0.01:10;
y=normpdf(x,0,1);%正态分布函数。
figure;
axes1=axes('Pos',[0.1 0.1 0.85 0.85]);
plot(x,y);
set(axes1,'YLim',[-0.01 0.43],'XLim',[-3 3]);
3、瑞利分布
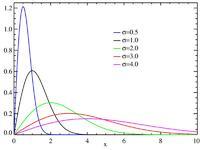
当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时,这个向量的模呈瑞利分布。瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型。两个正交高斯噪声信号之和的包络服从瑞利分布。
是不是感觉好抽象,有人问,为什么会产生瑞利分布?这是因为瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型,通信中很多信道的噪声满足这种分布,因此经常会用到。
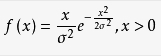
clear all;close all;
sigma=2; % 瑞利分布参数sigma
fs=1e7; % 采样率,单位:Hz
t=1e-3; % 随机序列长度,单位:s
t1=0:1/fs:t-1/fs;
n=length(t1);
rand('state',0); % 把均匀分布伪随机发生器置为0状态
u=rand(1,n); % 产生(0-1)单位均匀信号
x=sqrt(2*log2(1./u))*sigma; % 广义均匀分布与单位均匀分布之间的关系
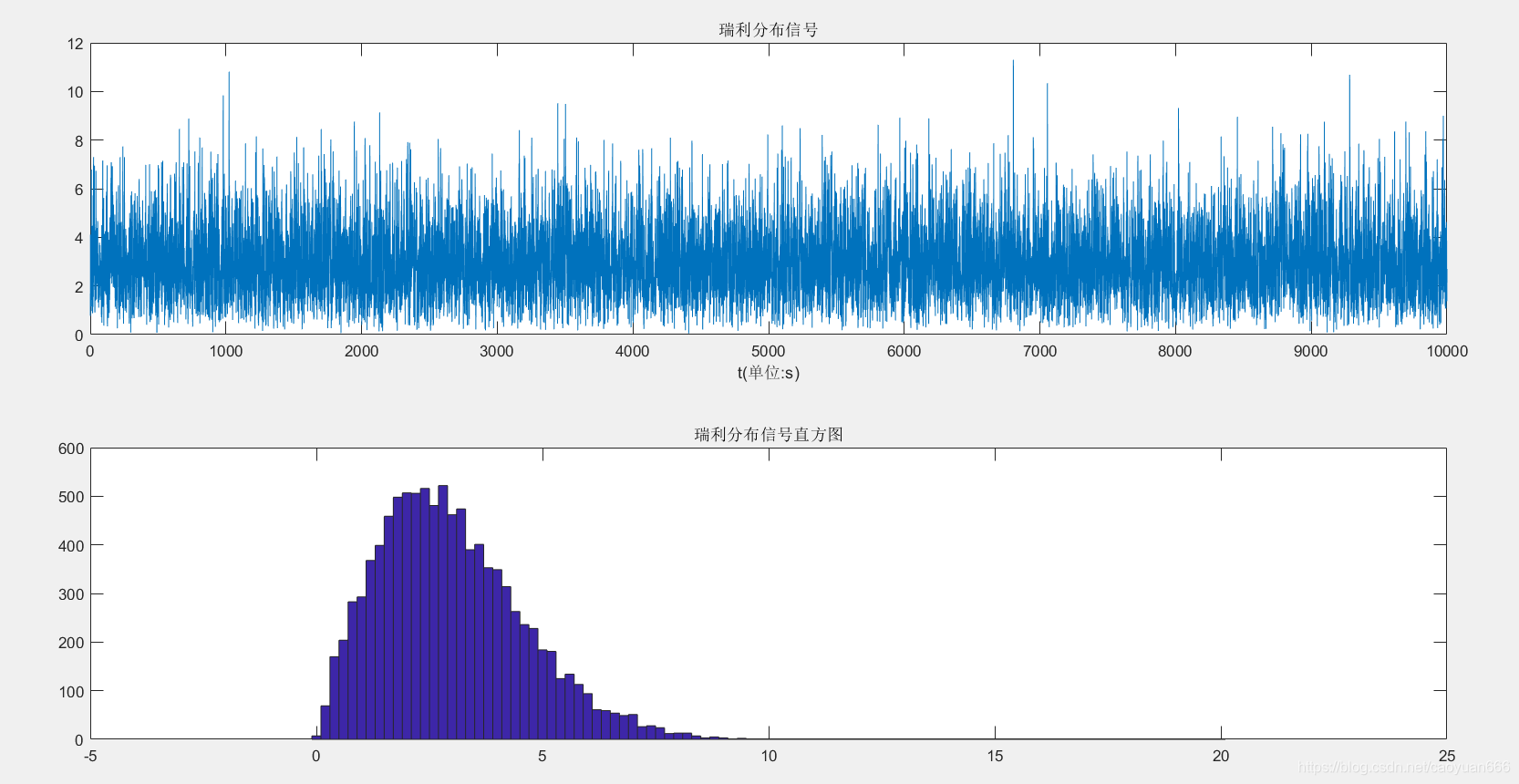
subplot(211);plot(x); % 输出信号图
xlabel('t(单位:s)');
title('瑞利分布信号'); % 输出信号的直方图
subplot(212);hist(x,0:0.2:20);
title('瑞利分布信号直方图');
4、莱斯分布
莱斯分布实际上可以理解为主信号与服从瑞利分布的多径信号分量的和。概率密度函数公式中,R即为正弦(余弦)信号加窄带高斯随机信号的包络,参数A是主信号幅度的峰值,σ^2是多径信号分量的功率,I0()是修正的0阶第一类贝塞尔函数。
是不是感觉这个更抽象了,那有什么用呢,在通信中,有一个信号占主要成分的噪声中,信道噪声一般呈现莱斯分布。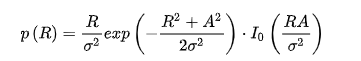
N = 100000;
K = 0.5;
const=1/(2*(K+1));
x1=randn(1,N);
x2=randn(1,N);
x=sqrt(const*((x1+sqrt(2*K)).^2+x2.^2));
[y,xi] = ksdensity(x);
plot(xi,y, 'bo')
% 验证
hold on
sig = 1;
v = 1;
yn = zeros(size(xi));
k=find(b > 0 & xi >= 0);
if any(k),
xk = xi(k);
% Rician分布的概率密度函数
yp(k) = (xk ./ sig^2) .* exp((-xk.^2 + v.^2) ./ (2*sig^2)) .* besselj(0, (xk .*v ./ sig^2));
end
plot(xi,yp,'b')
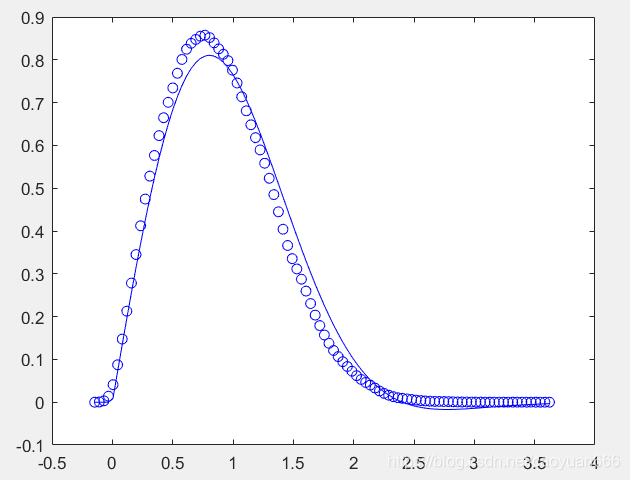
至此,均匀分布、高斯分布、瑞利分布、莱斯分布就大体介绍完毕!