Laplacian Eigenmaps

作者：xu kaihe
链接：https://zhuanlan.zhihu.com/p/25096844
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

接着写数据降维算法。上一篇文章介绍了 PCA, Factor Analysis, LLE 等三个算法, 按照顺序这篇文章就该讲到 Laplacian Eigenmaps 了,但是作者认为直接讲 LaplicanEigenmaps 好像有点太干了, 不太容易理解, 请允许我夹带点私货, 先从 Graph Laplacian 开始讲起 (graph Laplacian 是 graph theory 中的一系列算法的总称,因大量使用 Laplacianmatrix 而得名), 然后找个恰当的时机讲 Laplacian EM, 毕竟它们之间有千丝万缕的联系。

在作者读书生涯中的很长一段时间里, Graph Laplacian 一直像是黑魔法一样的存在。相信很多同学都听说 "number of zero eigenvalues" 跟 "second smallest eigenvalue" 这俩概念, 这俩个参数炸一看根本不 make sense, 好像是一些不讲道理的参数, 0 的个数? 第二小? 不过下面我们会仔细分析 3 个问题, 通过这些问题来阐述 Graph Laplacian 背后的数学之美, 同时也解开黑魔法的秘密。这三个问题分别是:

connected components: 比如说下面这个图里面有 5 个 connected component, 如何分分钟知道 5 这个数字,并且找出每个 component 对应的顶点们
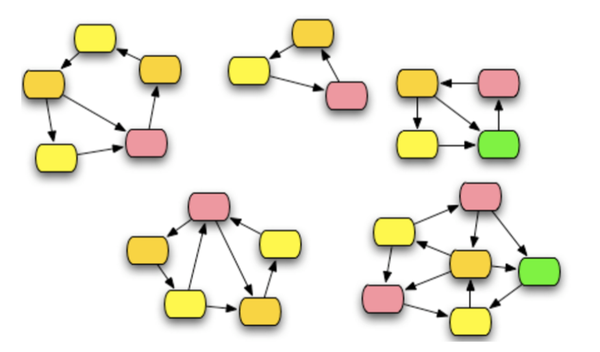
graph cut 问题:如何把一副图切成 k 个部分,令他们相互之间最为独立
graph spectral: 就是我们喜欢的降维问题

那就先从最简单的 connected component 开始。社交网络天然地就是一个无向图，假设每一个用户都是一个点，好友关系是两点之间的边，那么在整个社交网络中天然地存在很多独立的小圈子，这些小圈子里的用户只跟圈子内部的人来往，不跟外部来往，那么我们要如何找到这所有的这些独立的小圈子呢? 喊着眼泪写深度优先搜索吗? 这个典型的connected component问题可以用Graph Laplacian来解决，先构建它的邻接矩阵 (adjacency matrix), 构建方法如下图所示:

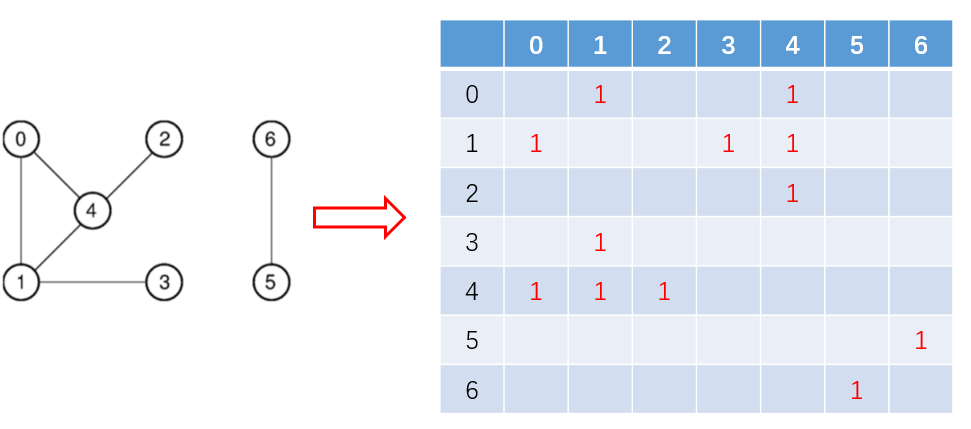
假设有 N 个顶点,邻接矩阵 W 的维度就是 N*N, 定义顶点的度(degree of a vertex): 与它相连的邻居个数。计算一个每个顶点的度然后可以得到一个相应的对角矩阵 D, 上面这副图相对应的 D 矩阵是这样的

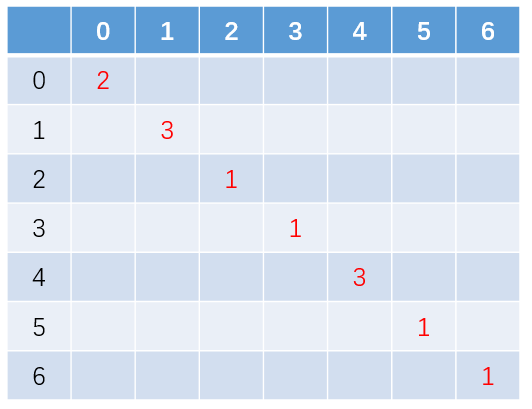
拿到了这俩矩阵,终于可以引出 Graph Laplacian 的定义: $L=D-W$ 先不谈为什么要这样定义,我们直接来看看矩阵 L 的性质: L 是个半正定矩阵 (positive semidefinatematrix) , 即对于任何向量 f, L 都能满足 $f'Lf\geq0$ 。下面让我们来尝试证明一下这个定理(原谅我的啰嗦,因为这个性质对理解黑魔法真的真的非常重要!)

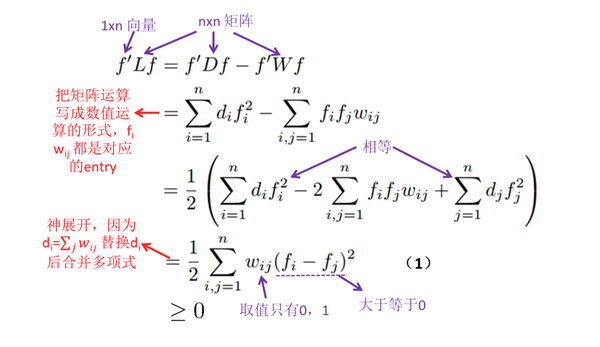
那么在什么情况下 $f'Lf$ 也就是 L 的特征值等于 0 呢? 根据式(1) 我们可以发现让它为 0 的条件是: 当且仅当 $w_{ij}=0$ 跟 $f_i=f_j$ 这俩条件至少满足一个。由于 graph 本身已经给定, $w_{ij}$ 我们是爱莫能助了,所以对于边不为 0 的两个顶点 (i, j) 只好让它们对应的 $f_i=f_j$ 了。

怎么样,读到这里是不是有种很微妙的感觉。没错,特征值 0 对应的特征向量一定是有类似这样的形式 (1,1,1,1,1,2,2): 连在一起的点取值必定一样! 于是我们就能分分钟找出所有的 connected component, 对着 eigenvector 按图索骥就行了。那么值为 0的 eigenvalue 的个数为什么就是 connected component 的个数呢? 这是因为如果有 M 个connected component, 那 eigenvector 有且仅有 M 种不同的取值。eigenvectors 当中模为 1的,并且互相之间线性独立的有且只有 M 种, 对应的就一定有 M 个为 0 的特征值。

理解了黑魔法 1,就可以很容易地理解黑魔法 2 了。黑魔法 2 想解决的是 graph cut 问题,也就是:给定一个图, 把它的顶点们分成 A,B 两个部分, 令这两部分之间的联系最小。也就是这样一个优化问题:

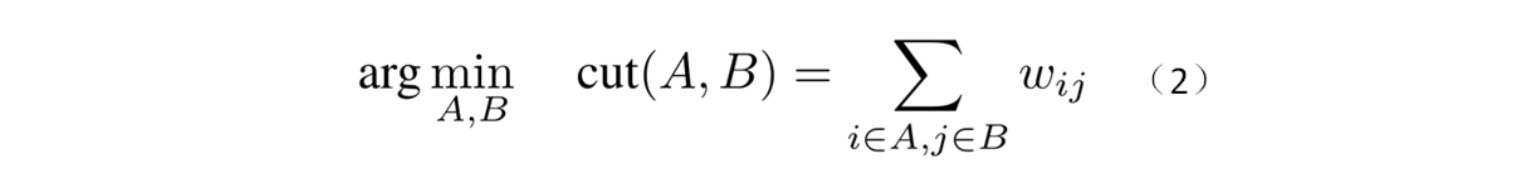
问题(2)一点都不好解,因为优化变量是 “把顶点们分成两部分”,根本没法求导。于是天才们把这个问题做了一个变形:

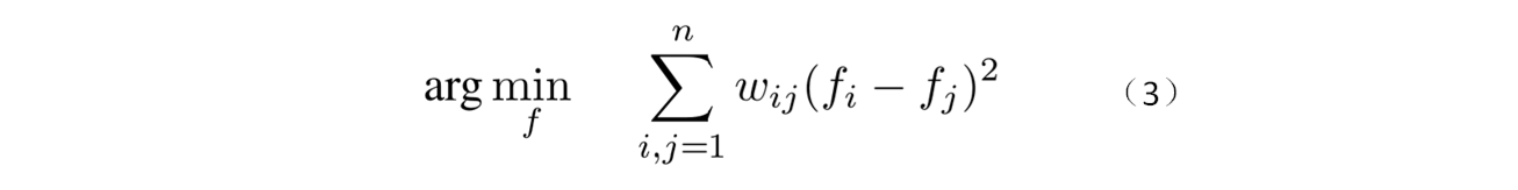
这样就利索多了,变量成了一个向量 f。为什么可以这样变形呢?请看问题(3),假设边 (i,j)的权重非常大,我们就只好尽量地让 $f_i\approx f_j$ 来减少 $w_{ij}$ 造成的损失。如果可以令 f 的每一个 entry 都只能从 0 或 1 之间取值, 那么问题(3)就完全地等同于问题(2)。但不幸的是这样以来问题(3)就成了 NPhard 问题。黑魔法 2 其实只是问题(3)的一个近似解:对 L 做SVD 分解,找出 second smallest eigenvalue,设定一个 threshold, 比它大的 entries 分到 A类,比它小的 entries 分到 B 类。举栗说明:

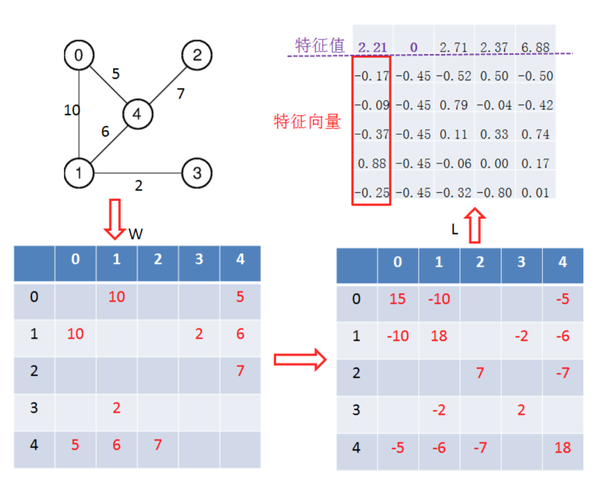
大家通过这个栗子就知道为什么黑魔法 2 执着于 second smallest eigenvalue, 因为 thesmallest eignevalue 是 0 啊! 表示这副图是全连通图。有了特征向量就可以设个 threashold就能把图分成两部分, 以此类推, 想分三部分的话就设俩 shreashold 喽。是不是很神奇呀,不过这种单纯的方法很容易就会把图给 cut 成一个很大的部分跟一个孤立的点,就像上面这个栗子里面的顶点 3。为了解决这个问题天才们又提出了 balancedcut 的思想, 例如 ratiocut。有兴趣的同学可以自行 google。

绕了这么大一个圈,终于把私货都放出来了。下面开始进入今天的主题,LaplacianEigenmaps。面对 N 个维度为 m 的样本,希望可以把它们降到 k 维(k<m)。不过首先我们要把样本们转化成一张图。一般来说有两种思路可以完成这一步: 1. 对于每个顶点,找到距离它最近的 k 个邻居, 每个邻居用下面这个高斯函数计算边的权重; 2. 以每个顶点为中心画一个半径为 R 的球, 所有在这个球里面的点都是邻居,用下面这个高斯函数计算一下权重。

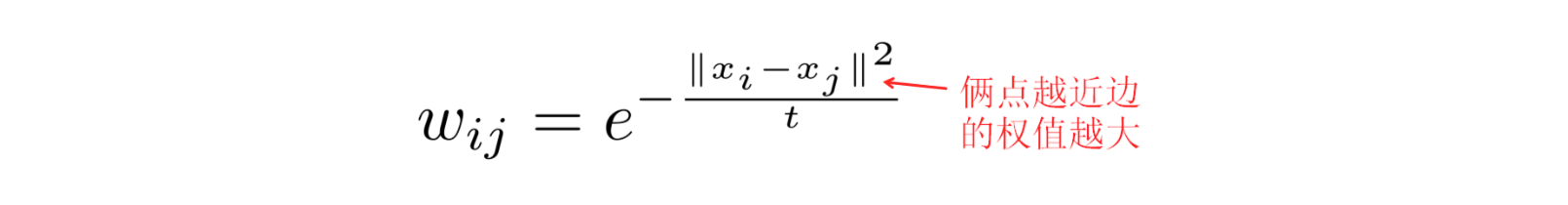
于是就有了一个 graph,然后就可以用 Laplacian 三板斧了: 1. 计算 L; 2. 把 L 做SVD分解; 3. 找出 top k+1 最小的 eigenvalue, 去掉为 0 的那个, 就能得到对应的 k 个维度为 1*N 的向量, 变成 N 个 k*1 的向量就是降维之后的点。

我们不禁要问, 这样做有什么道理呢? 原理其实就来自黑魔法, 黑魔法 2 可以把一个图给cut 成高内聚,低耦合的一个个块, 所以如果数据在原空间里团在一起, 他们所对应的eigenvector entry 的取值也会很类似, 所以到了低维空间里面他们还是团在一起的。这就是我们想要保留的聚类特性。蛋卷图:

结论:Laplacian EM 的性能看上去跟 LLE 有点类似,都能把蛋卷给展开,从而让数据点在低维度上线性可分。到这里我们就讲完了着重于局部的降维算法,下面的四个算法再下回分解把。

编辑于 2017-02-09

猜你喜欢