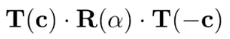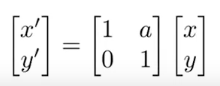图形学笔记（三）变换——缩放、镜像、切变

图形学笔记（二）图形学中的线性代数——向量、矩阵（转置、逆）、叉乘、点乘
图形学笔记（四）变换——三维变换（三维旋转与欧拉角）、MVP变换、视图变换、投影变换（正交投影与透视投影）

1. 缩放(Scale)变换

1.1 均匀缩放

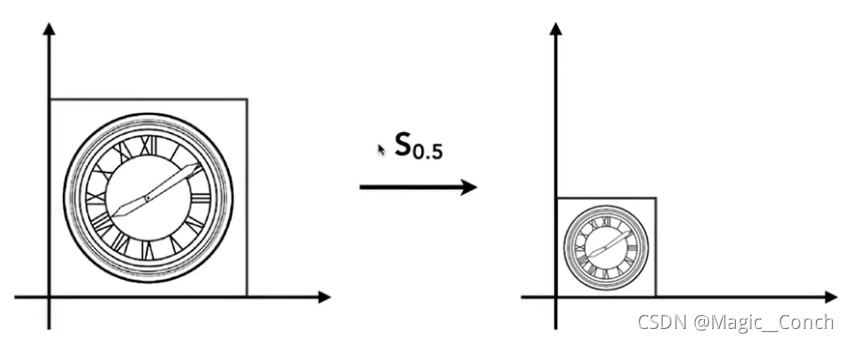
1. 代数形式：
   $$\begin{gathered} x^{{}^{\prime }}=sx \\ {y}^{{}^{\prime }}=sy \end{gathered}$$
2. 矩阵形式：
   
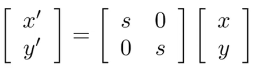
   其中，缩放矩阵：
   $$\left(\begin{array}{cc}s& 0\\ 0& s\end{array}\right)$$

1.2 不均匀缩放

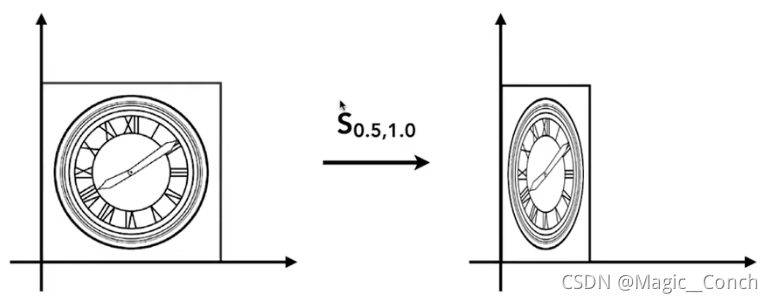
对应的缩放矩阵：

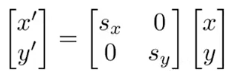
2. 镜像(Reflection)变换

水平镜像：

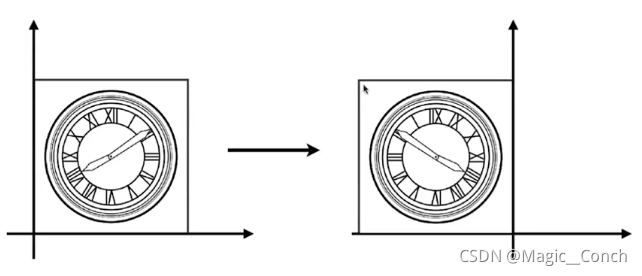
1. 代数形式：
   
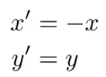
2. 矩阵形式：
   

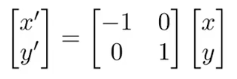
3. 切变Shear

切变：两个距离很近、大小相等、方向相反的平行力作用于同一物体上所引起的形变。
Tips：
y=0时，水平方向的变化是0；
y=1时，水平方向的变化是a；
整张图竖直方向的变化总是0。
矩阵变换：

4. 旋转

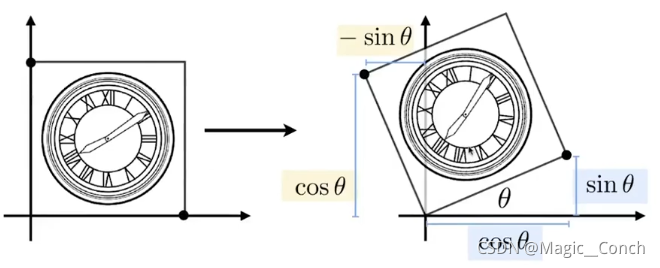
Tips：旋转默认是以(0,0)为中心，默认是逆时针方向。

4.1 旋转矩阵及性质

旋转Rotation矩阵：
$$R_{\theta }=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$$
当角度为负数时（将$-\theta$代入），说明旋转矩阵是正交矩阵：
$$R_{\theta }=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)=R_{\theta }^T$$
可以得到旋转矩阵的以下性质：
$$R_{-\theta }=R_{\theta }^{-1}$$

4.2 推导

选两个原位置为(1,0)和(0,1)的特殊点，使二维矩阵待定系数，使用三角函数求解。

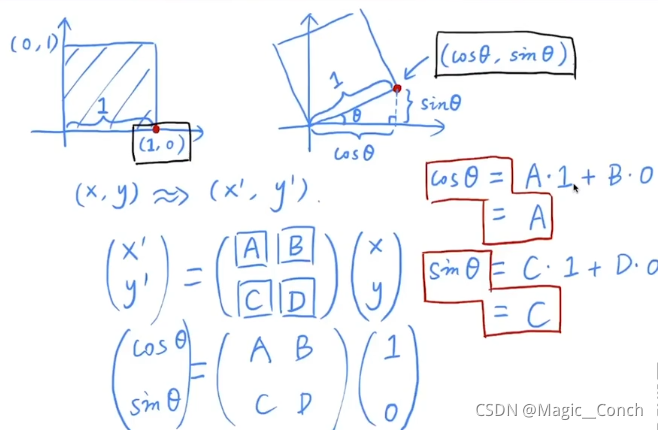
5. 线性变换(Linear Transforms)

线性映射（ linear mapping）是从一个向量空间V到另一个向量空间W的映射且保持加法运算和数量乘法运算，而线性变换（linear transformation）是线性空间V到其自身的线性映射。

线性变换（Linear Transforms） = 矩阵(Matrices)。
线性变换都可以写成矩阵相乘的形式，如下所示：

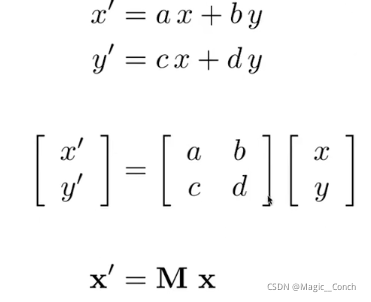
6. 齐次坐标(Homogenous Coordinates)：

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。

6.1 引入

平移变换：

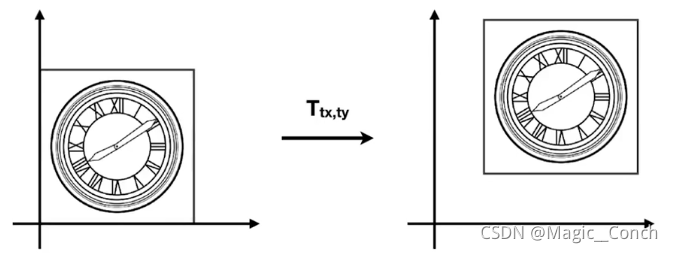
1. 平移变换的表示形式：
   

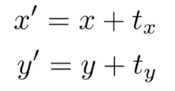
2. 存在的问题：以上的写法不能写成矩阵形式。
   只能写成以下形式：
   

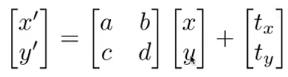
这里平移不再是线性变换，所以有没有办把包括平移在内的所有变换表示出来的统一方法呢？
解决办法：齐次坐标。

6.2 齐次坐标

6.2.1 齐次坐标的二维表示

对于二维坐标，增加第三个维度：
$$二维的点=(x,y,1{)}^T$$
$$二维的向量=(x,y,0{)}^T(0是使得平移变换之后方向不变）$$

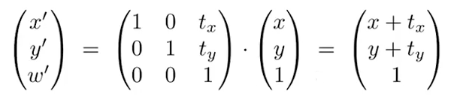
6.2.2 点和向量第三维为0和1的验证：

如果点的第三维为0，那么点和向量运算保持了平移不变性（点+向量第三维不会超过1）。

6.2.3 点齐次坐标的意义

在齐次坐标下，点+点是这两个点的中点，如下所示（相加w变成2，然后横纵坐标全除以2）。

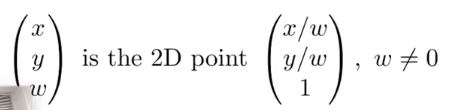
7. 仿射(Affine)变换

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。

7.1仿射变换的两种表示形式

1. 线性映射+平移
   

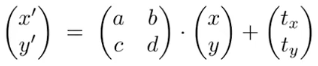
2. 齐次坐标的形式
   

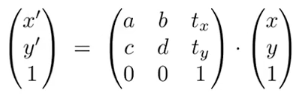
7.2 齐次坐标表示各种变换

1. 缩放
   
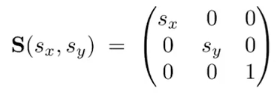
   2.平移
   
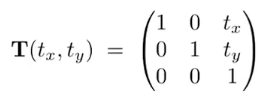
   3.旋转
   

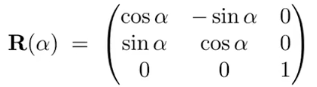
8. 逆(Inverse)变换

表示为：$M^{-1}$
$M^{-1}$在矩阵和几何意义上都是是变换M的逆。
简单的理解：把变换的操作反过来，如下图所示。

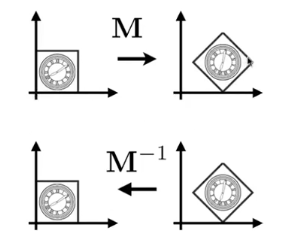
9. 变换组合(composite)：

如何得到以下变换？

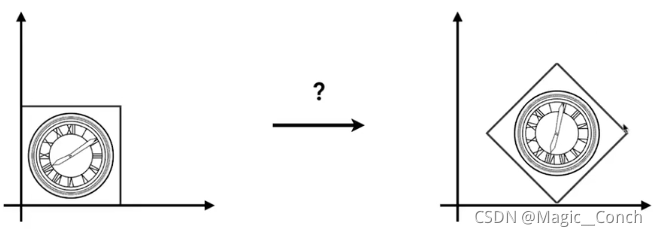
先平移再旋转，得到的结果是不对的：

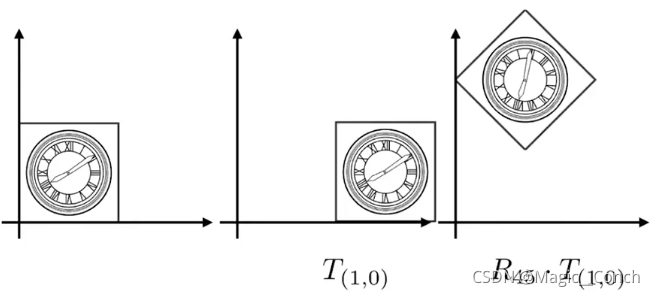
先旋转再平移，得到正确的结果：

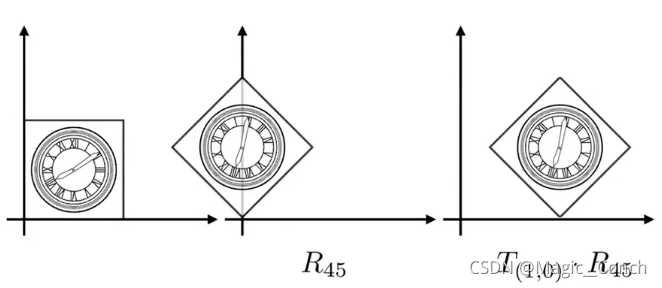
可以知道：

1. 复杂的的变换可以通过简单的变换得到。
2. 变换的顺序非常重要（矩阵乘法不满足交换律）。
3. 矩阵是从右到左应用的。如下所示，先旋转再平移。
   

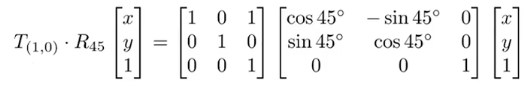
结论的推广（矩阵乘法满足结合律）：

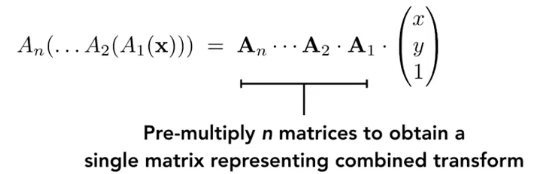
将不同的变换矩阵进行合成：对于很多变换，可以先把变换做乘积，得到一个3*3的矩阵来表示十分复杂的矩阵。

10. 变换的分解：

例子：让矩阵按照某一点进行旋转（如下所示，先将旋转点平移到原点，然后再平移回去）。

变换矩阵的表示形式：