川川数模-D5-图的最短路径和距离

问题：
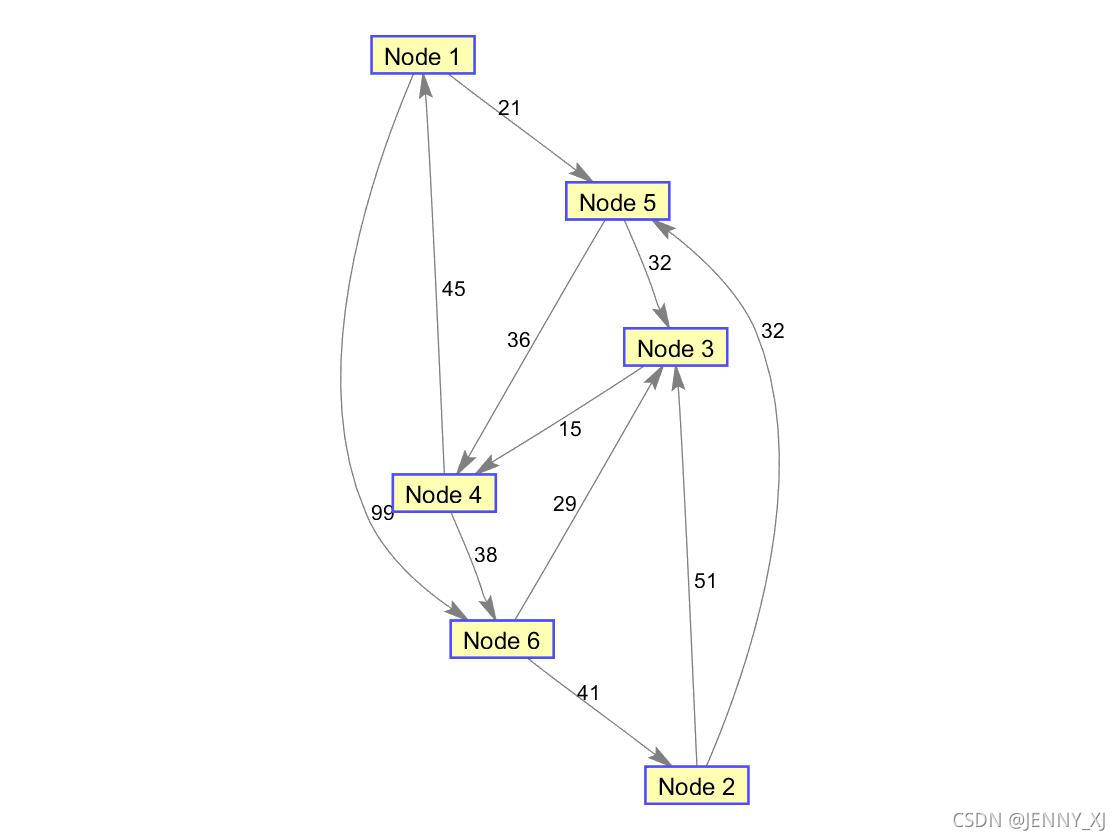
有向图：

无向图：

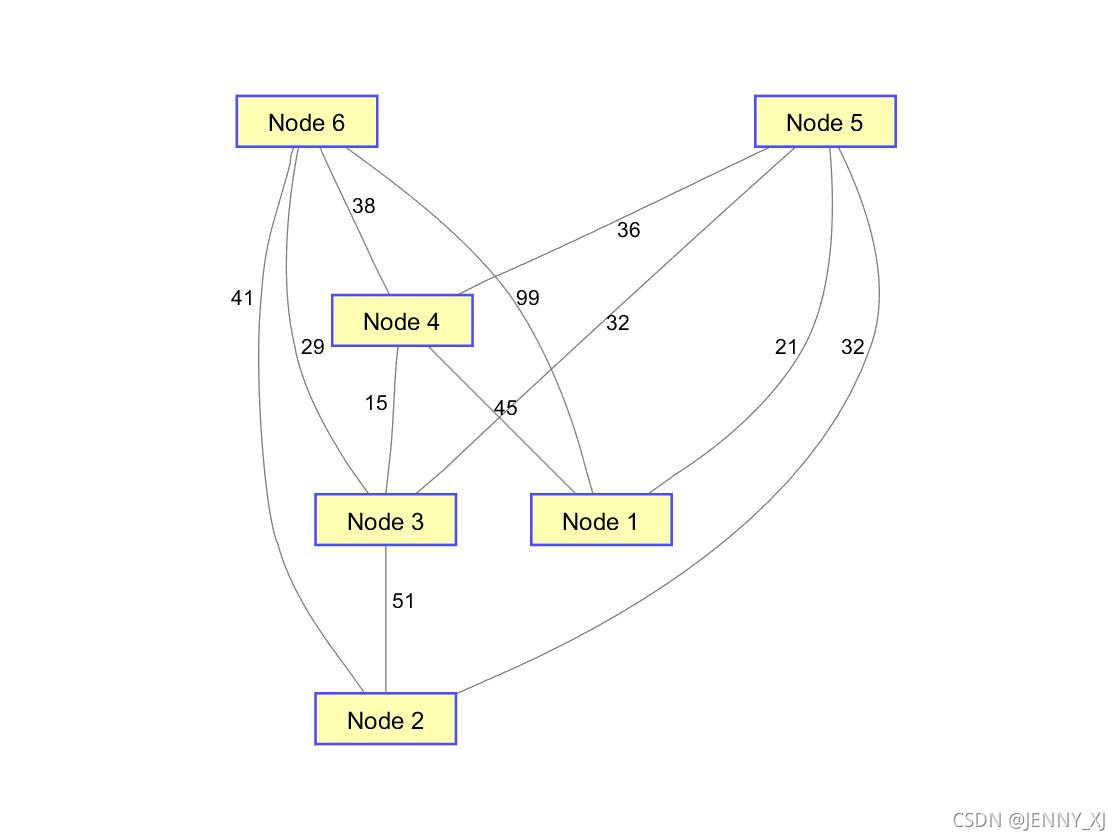
创建稀疏矩阵sparse

方法一

%w(起点,终点)=权重值
clear all
clc
w=zeros(4);
w(1,2)=2;w(1,3)=3;w(1,4)=8; 
w(2,3)=6;w(2,4)=6;
G=sparse(w)

方法二

clear all
clc
%sparse([起点集合],[对应终点集合],[对应权重集合])
G = sparse([1 1 1 2 2],[2 3 4 3 4],[2 3 8 6 6]);
s=sparse(G)

有向图的最短路径

方法一
graphallshortestpaths

其中G为稀疏矩阵； 0/false:无向图； 1/true:有向图;

clear all
clc
G = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 29 21])
view(biograph(G,[],'ShowWeights','on'))
graphallshortestpaths(G)

返回结果：

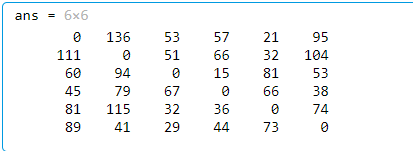
返回的矩阵中对应的数值为最短路径，及A_ij为i节点到j节点的最短路径。但是这种方法无法直观地反映出最优路径。

方法二
dijkstra.m
函数为：

function [min,path]=dijkstra(w,start,terminal)
n=size(w,1); label(start)=0; f(start)=start;
for i=1:n
   if i~=start
       label(i)=inf;
end, end
s(1)=start; u=start;
while length(s)<n
   for i=1:n
      ins=0;
      for j=1:length(s)
         if i==s(j)
            ins=1;
         end
      end
      if ins==0
         v=i;
         if label(v)>(label(u)+w(u,v))
            label(v)=(label(u)+w(u,v)); 
         f(v)=u;
         end 
      end
   end   
v1=0;
   k=inf;
   for i=1:n
         ins=0;
         for j=1:length(s)
            if i==s(j)
               ins=1;
            end
         end
         if ins==0
            v=i;
            if k>label(v)
               k=label(v);  v1=v;
            end
         end
   end
   s(length(s)+1)=v1;  
   u=v1;
end
min=label(terminal); path(1)=terminal;
i=1; 
while path(i)~=start
      path(i+1)=f(path(i));
      i=i+1 ;
end
path(i)=start;
L=length(path);
path=path(L:-1:1);

调用函数：

% 构造邻接矩阵
a = zeros(6);
a = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 29 21])
a = a + a';
a(a==0) = inf; % 零元素换成inf
a(eye(6,6)==1)=0; % 对角线换成 0 
view(biograph(a,[],'ShowWeights','on'))
[min,path]=dijkstra(a,1,6) % dijkstra模型求解节点一到节点六最短路径

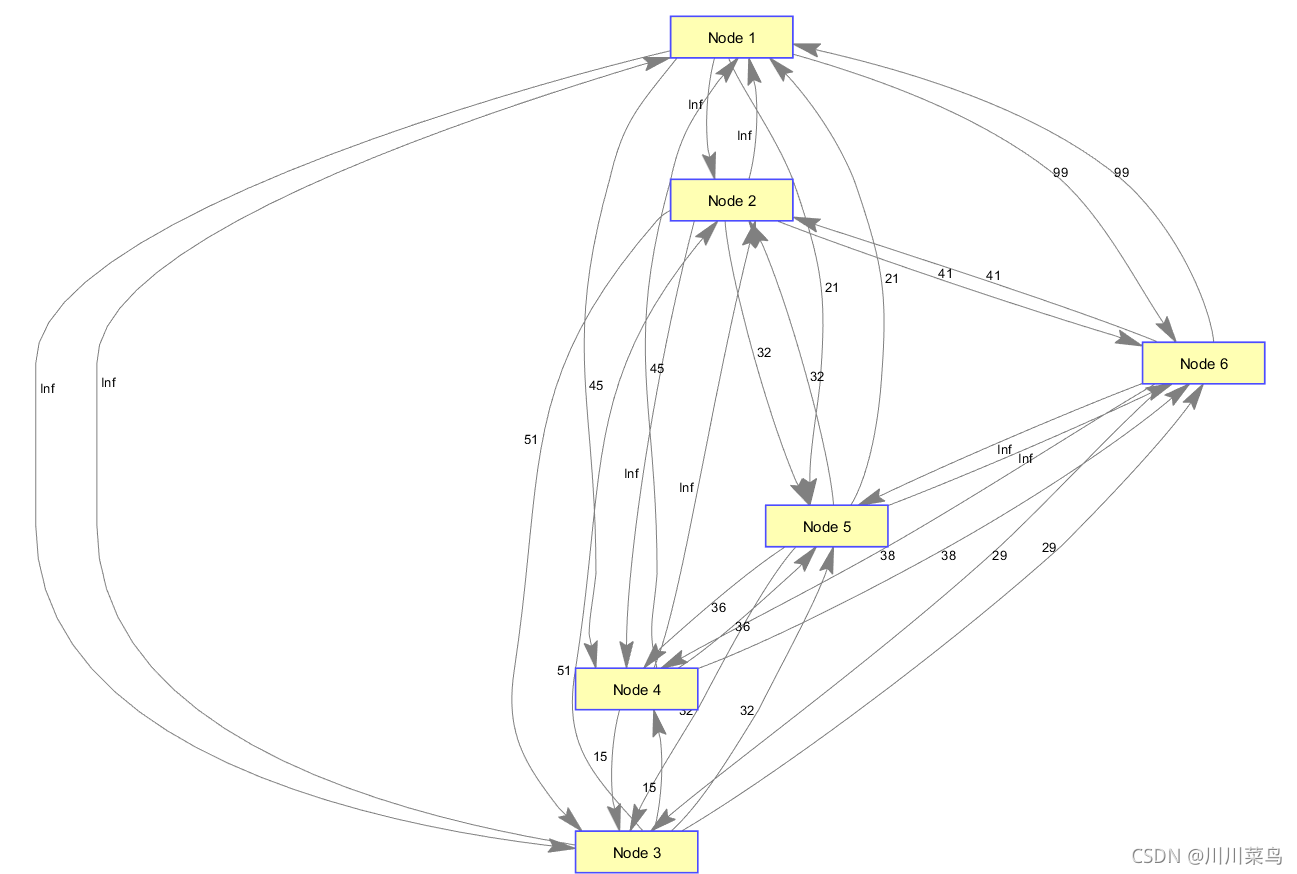
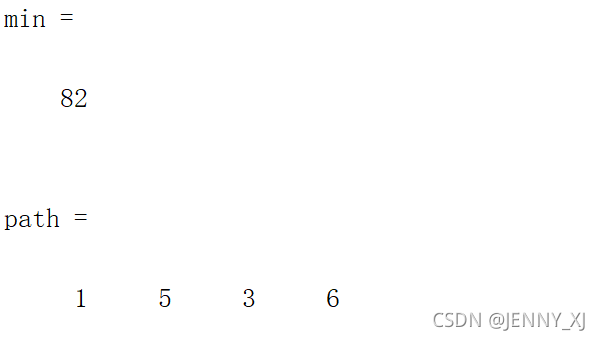
无向图的最短路径

方法一
graphallshortestpaths

clear all
clc
W = [41 99 51 32 15 45 38 32 36 29 21];
G = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],W);
UG = tril(G + G')
view(biograph(UG,[],'ShowArrows','off','ShowWeights','on'))
graphallshortestpaths(UG,'directed',false)

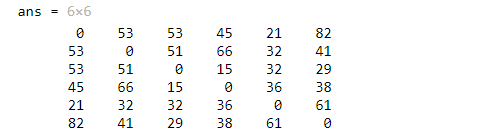
方法二
shortestpath

clc
clear all
% 构造邻接矩阵
G = zeros(6);
G = graph([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 29 21])

plot(G,'EdgeLabel',G.Edges.Weight)
[P,d] = shortestpath(G,1,6)

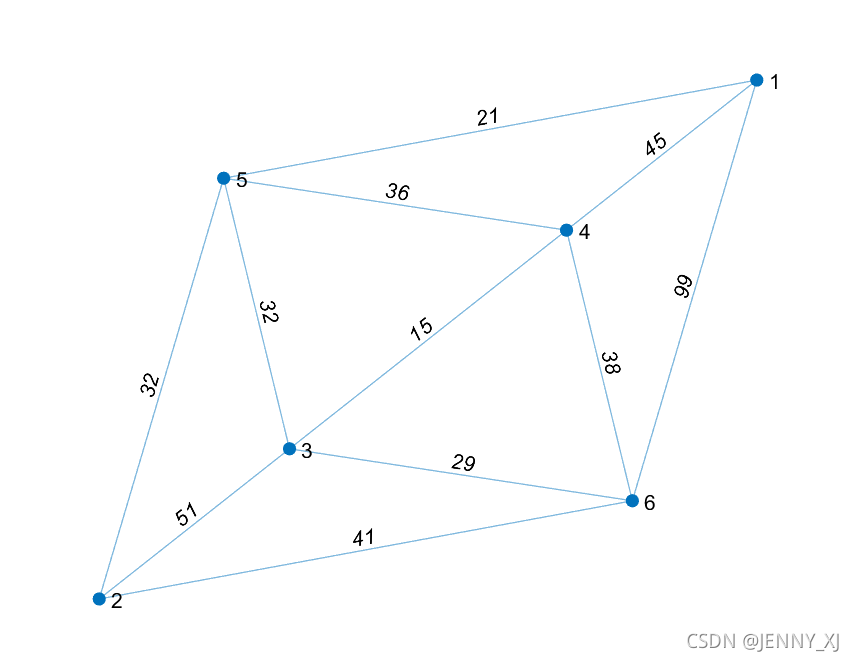
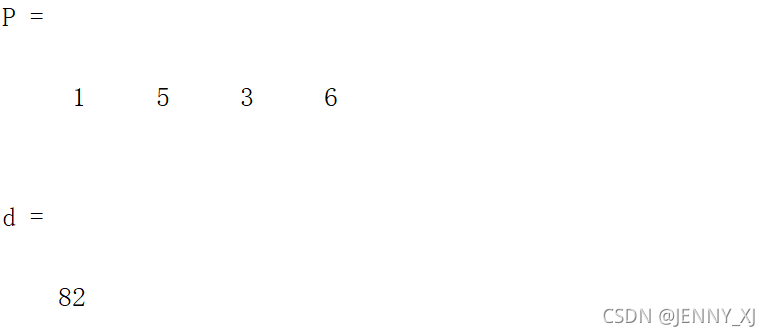
P为最优路径，d为最优路径的返回值。