Radon–Nikodym theorem

In mathematics, the Radon–Nikodym theorem is a result in measure theory that expresses the relationship between two measures defined on the same measurable space. A measure is a set function that assigns a consistent magnitude to the measurable subsets of a measurable space. Examples of a measure include area and volume, where the subsets are sets of points; or the probability of an event, which is a subset of possible outcomes within a wider probability space.

One way to derive a new measure from one already given is to assign a density to each point of the space, then integrate over the measurable subset of interest. This can be expressed as

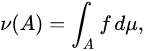
where ν is the new measure being defined for any measurable subset A and the function f is the density at a given point. The integral is with respect to an existing measure μ, which may often be the canonical Lebesgue measure on the Real line ℝ or the n-dimensional Euclidean space $R^n$ (corresponding to our standard notions of length, area and volume). For example, if f represented mass density and μ was the Lebesgue measure in three-dimensional space $R^3$, then ν(A) would equal the total mass in a spatial region A.

The Radon–Nikodym theorem essentially states that, under certain conditions, any measure ν can be expressed in this way with respect to another measure μ on the same space. The function  f  is then called the Radon–Nikodym derivative and is denoted by $\frac{d\nu }{d\mu }$. An important application is in probability theory, leading to the probability density function of a random variable.

The theorem is named after Johann Radon, who proved the theorem for the special case where the underlying space is $R^n$ in 1913, and for Otto Nikodym who proved the general case in 1930.[2] In 1936 Hans Freudenthal generalized the Radon–Nikodym theorem by proving the Freudenthal spectral theorem, a result in Riesz space theory; this contains the Radon–Nikodym theorem as a special case.[3]

A Banach space Y is said to have the Radon–Nikodym property if the generalization of the Radon–Nikodym theorem also holds, mutatis mutandis, for functions with values in Y. All Hilbert spaces have the Radon–Nikodym property.

1. Formal description

2. Examples

3. Properties

https://en.wikipedia.org/wiki/Radon%E2%80%93Nikodym_theorem