

题意:有nn的格子,然后在一个点的8个方向中的其中任意一个方向上的延长线上最多只能有1个皇后(意思就是可以有0个或者1个)
图理解:
比如题上的66的格子;
那么有:
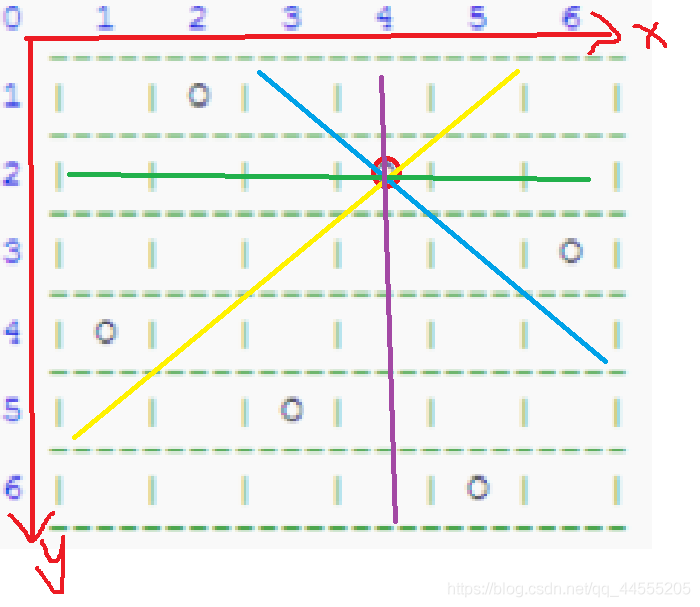
就是这8个方向;每一种颜色线上最多出现一个皇后,问一共有多少种放皇后的不同方案(指方案所形成的图形不会完全一样);
现在题意清楚了;
那么这个题有个难点在于怎么判断这个点是否能够走(8个方向上是否已经存在1个皇后了)?又应该怎么走?
通过找规律可以发现这个问题:
1.对于向右斜的黄线,它每个格子上的x坐标+y坐标是一个定值;所以平行于黄线的线上面也有同样的规律;
2.对于向左斜的蓝线,它每个格子上的x坐标-y坐标是一个定值;所以平行于蓝线的线上面也有同样的规律;
3.每行,每列最多放1个皇后,那么我就可以通过枚举每列是放还是不放皇后,然后在dfs里面深度搜索对应的列,然后确定这个位置合法之后才放;
但是对于2问题有个缺陷,就在于x-y可能是负数,所以这里可以给他+n(其实+一个大的正整数也行,只不过数组会开的大一点);
所以这个问题就有思路了;枚举每一列,然后dfs枚举行,确定列和行之后,就可以判断是否8个方向合法了;开始我担心TLE,但是手写了一下情况很少,因为8个方向有被限制;所以不会是n!种;
AC代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int r[2000],ma[5200],sa[5000];//分别用来判断是否行合法,主对角是否合法,负对角是否合法
int ans[20];//记录排列答案
int t;
void dfs(int queen){
//这里参数为什么是queen是因为这里的queen就相当与x坐标,因为每一列都必须有一个皇后,所以参数传这里
if(queen==n+1){
if(t<3){
for(int i=1;i<=n;i++)printf("%d%c",ans[i],i==n?'\n':' ');//按照dfs求全排列可以知道前三个就是字典序最小的,所以没有必要求出总的排列然后再去求字典序最小的
}
t++;
return ;
}
for(int y=1;y<=n;y++){
if(!r[y]&&!ma[queen+y]&&!sa[queen-y+n]){
//第y行可以放并且主对角,副对角也可以放
r[y]=ma[queen+y]=sa[queen-y+n]=1;//标记已经放过了
ans[queen]=y;//在queen列上面的y行放一个
dfs(queen+1);//判断下一行是否能够放
r[y]=ma[queen+y]=sa[queen-y+n]=0;//撤销标记
}
}
}
int main(){
scanf("%d",&n);
dfs(1);//从第一列开始
printf("%d\n",t);
return 0;
}