
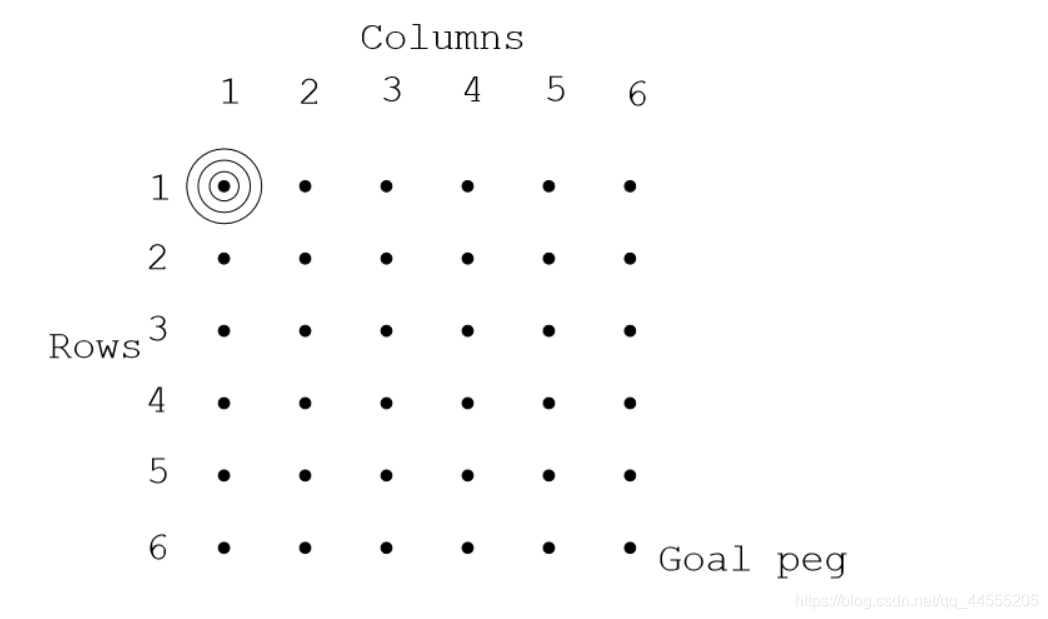

题意:给出一个nn格式的钉子和d个从上往下size逐渐增大的disk(放在(1,1)坐标处),问在把d个disk全部移动到(n,n)坐标的时候最少的移动次数是多少,当然题目也有限制条件:
1.每个钉子上只能放一个(除开第一个和最后一个)。
2.只能往下移动或者右边移动;
这道题算是签到题吧。。我自己把题目读错了,我想成了一个钉子可以放多个。。。。。无语了。。。
其实把题理解到位了,写两下就可以发现规律;
因为d个disk都要从左上角,移动到右下角,那么是不是不管怎么移动,最后一个肯定存在一个移动路径到最右下角;
那么可以举例33的一个矩阵;
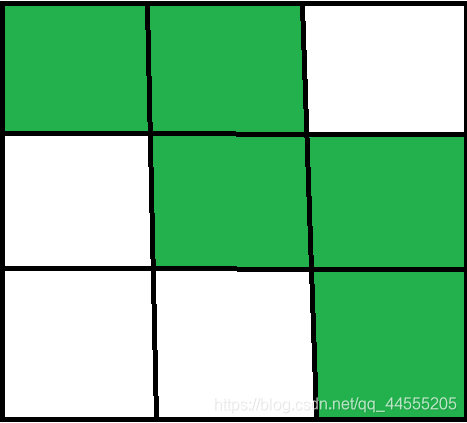
那么最大个那个盘就是上面绿色部分的移动路径;然后我们可以发现在这个矩阵中,如果d=1,d=2,d=3=d=4,d=5是都成立的;
然后当d=6的时候就有问题了;
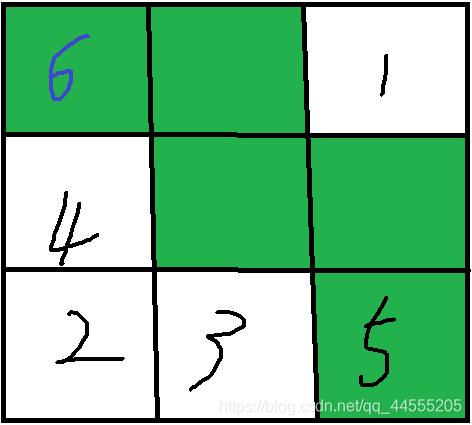
这样肯定就是移不动了;
因为最大的disk移动到终点时,所走过的格子数目为2*(n-1)(这里不包括起点),其余剩下的格子为nn-2(n-1),因为我们需要空一个出来才能走到所以如果d的数目大于等于了nn-2(n-1)+1那么就是不可能了;也就是意思:
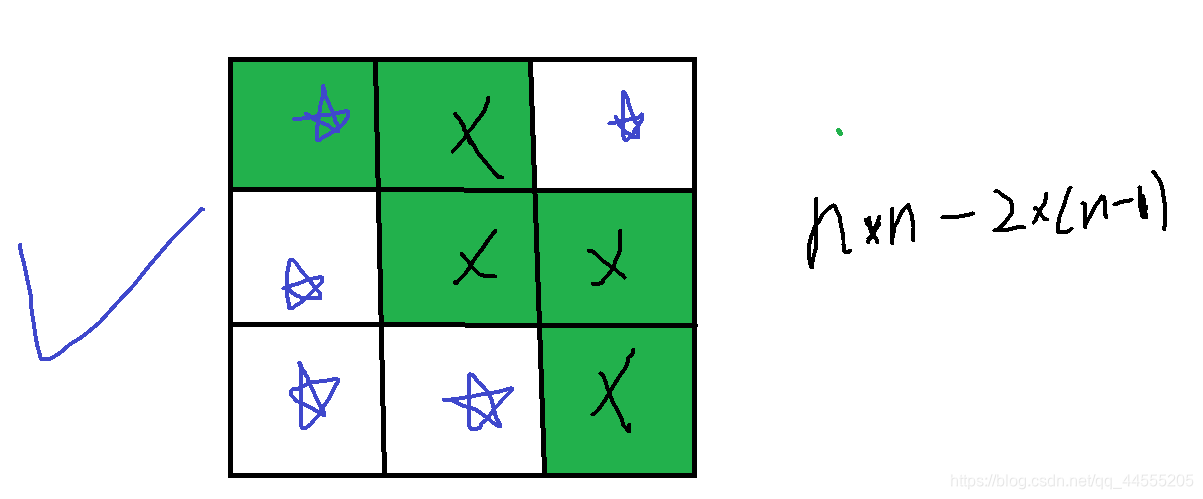
星号是disk,叉叉是空位子,如果d>=nn+2(n-1)+1那么久impossible;
所以AC代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
int T;
scanf("%d",&T);
int g=1;
while(T--){
int d,n;
scanf("%d %d",&d,&n);
if(d>=n*n-2*(n-1)+1)printf("Grid #%d: impossible\n",g++);
else {
printf("Grid #%d: %d\n",g++,d*2*(n-1));
}
puts("");
}
return 0;
}