
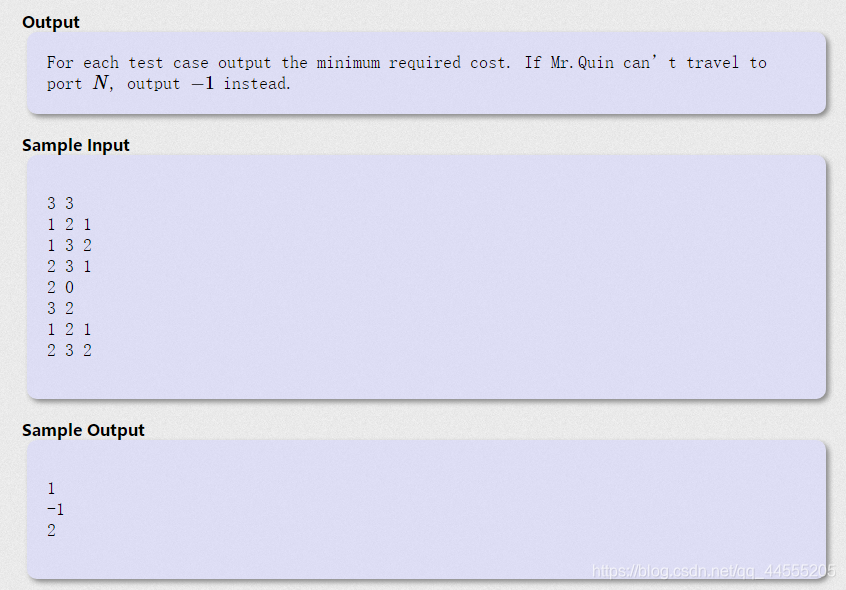
要解决这道题,可以用dfs+bfs,但是我不会,所以我只会dijkstra算法;
要解决这道题必须明白迪杰斯特拉算法的核心思想,我是这样理解的:
我可以任意举例一个图: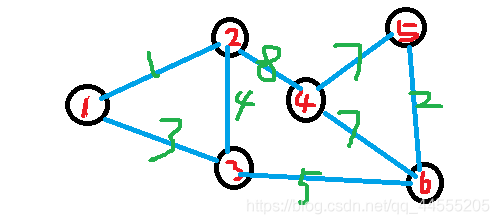
比如这个图,那么求1—6的最短路径;当然因为这个点很少可以用二维数组来存储;
Dijkstra思想:我先利用dis[]数组来存下1能到达的所有点的距离,然后其他点置为INF(通常INF令为0x3f3f3f3f就够了);
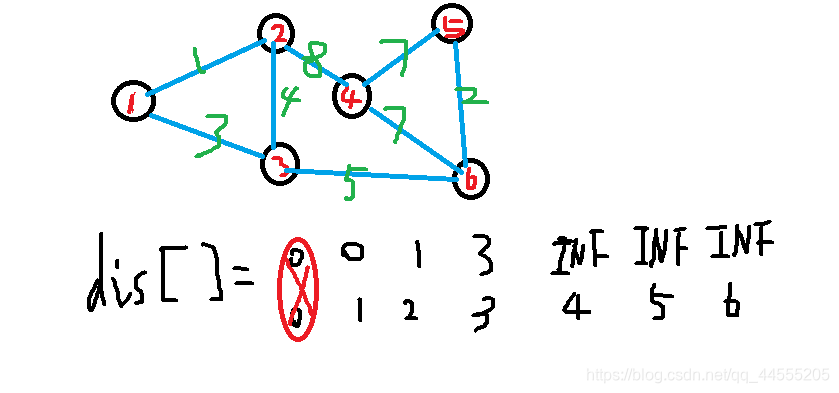
然后我就可以利用现有能达到的点作为中转站然后找其他能到达的点,然后每次更新dis数组值;
比如:我们从2点开始,枚举出所有2能到达的点(当然因为1已经找过了所以应该用一个数组book[1]=1标记它已经走过了);
那么2能到的就只有4 和 3,那么然后比较 1到4的距离(INF)和1到2到4的距离(1+8),因为小于INF所以dis[4]就更新为9;
同理堆3也一样,之后每次当过中转站的点都被标记,因为不可能重复走呗。
那么问题来了,如何去是想这个思想呢?
首先我应该明确一点,除了第一个点之外的其它点都会作为中转站,那么大的for循环就是1—n-1个点,注意:这里大的for只是用来表示每个点需要作为中转站;和里面的内容没有必要的逻辑联系;
所以最简单的Dijkstra算法就出来了(因为这个算法并不考虑数组过大的情况):
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
int Map[1000][1000],n,m;//Map用来记录a点到b点的路径值,n表示有多少个点,m表示给出多少条边
int dis[1000],book[1000];//dis是用来表示 start点到其他点的距离,book用来标记 循环到这个点的是否被标记过
void dijkstra(int start){//最简单的dijkstra算法(采用矩阵形式)
//首先求出这个点到其他点的距离用一个for
int Min=INF;
for(int i=1;i<=n;i++){//初始化从start这点开始的所有能与start点可达的点的距离
dis[i]=Map[start][i];//注意这里dis和Map只是一个逻辑关系相联系
}
//这里需要枚举n-1个点,因为开始点不需要算
//所以用一个大的for来循环
book[start]=1;//标记开始点已经作为中转站过了
for(int i=1;i<=n-1;i++){
//找出第一个到start的最短的点
//并且标记已经选过了
Min=INF;
int u;//记录到start最短的点
for(int j=1;j<=n;j++){
if(book[j]==0&&dis[j]<Min){//去搜寻能与start有直接边的点的最小距离//这里最好头脑里面想着无向图
Min=dis[j];
u=j;
}
}
book[u]=1;//表示u这个点已经作为中转站了
//然后找到以u点为中转站的其他点到start的距离和经过u这个点的距离,并比较大小
for(int e=1;e<=n;e++){//这里e是end的简写,方便理解表示以u作为中转站所能到达的另一个点
if(Map[u][e]<INF){
if(dis[e]>dis[u]+Map[u][e]){//这就是上面分析的比较
dis[e]=dis[u]+Map[u][e];
}
}
}
}
}
void init(int n){
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++){
if(i==j) Map[i][j]=0;//自己到自己就是0
else Map[i][j]=INF;//其他的设为INF
}
}
}
void read(int m)//这里用来输入,因为函数分开写更好理解它的功能
{
int a,b,c;
for(int i=1;i<=m;i++){
cin>>a>>b>>c;
Map[a][b]=c;//令为无向图
Map[b][a]=c;
}
}
int main(){
cin>>n>>m;
init(n);//这里虽然n,m为全局变量,但是这样写参数传递更加好理解;
read(m);
dijkstra(1);//从第一个点开始(当然这里也可以从别的点开始)
for(int i=2;i<=n;i++){//输出到其他点的最短距离
cout<<"1到"<<i<<"的最短距离为:"<<dis[i]<<"\n";
}
cout<<endl;
return 0;
}
按照上图结果就是这样的: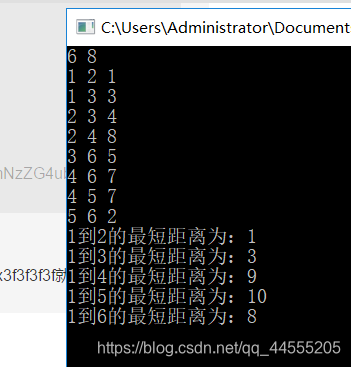
那么上面的只是最简单的Dijkstra算法,对于AC 这个题还远远不够,那么怎么优化呢?
这里就会用到优先队列+结构体+邻接表+Dijkstra;想想都很复杂,但是真真的理解了,还是很有用的;下边就是这道题的AC代码,但是我相信用了Dijkstra+堆优化,肯定在算法效率方面会有很大提高:
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
ll n,m;
struct End_Dis{
ll to,d,c;//to表示到的点,d表示到这个兵兵(也可以理解为距离问题),c用来记录是不是有这个兵兵在这条路上
End_Dis(ll a,ll b,ll cc=0):to(a),d(b),c(cc){}
bool operator < (const End_Dis tt) const{
return d>tt.d;//这个比较特殊,因为优先队列是由大到小,所以我写了一个由大到小的,然后这样会让优先队列由小到大排列(特别的地方)
}
};
vector<End_Dis> a[100000*2];
ll book1[200010];//用来标记这个点扫过没有
ll Dijkstra(ll start){
ll dis[200010];
for(ll i=1;i<=n;i++) dis[i]=INF;//先初始化为INF
book1[1]=0;//表示这个点走过了
dis[1]=0;//自己到自己距离为0;
priority_queue<End_Dis> q;//建立一个优先队列
q.push(End_Dis(1,0));//把第一个点放进去
while(!q.empty()) {//循环为非空
End_Dis t=q.top();
q.pop();
if(book1[t.to]) continue;//表示这个点使用过没有
for(ll i=0;i<a[t.to].size();i++){//以这个点位中转站,枚举其他点更新1----其他点的最短距离
End_Dis x=a[t.to][i];//取出对象
if((t.c!=x.d)+t.d<dis[x.to]) {//1到中转站h的距离+前面是否出现过的值是否小于 1---x的距离
dis[x.to]=(t.c!=x.d)+t.d;
q.push(End_Dis(x.to,dis[x.to],x.d));//找到了之后然后让中转站后面的点进队
}
}
}
return dis[n];
}
void read(ll m){
ll aa,bb,cc;
for(ll i=1;i<=m;i++){
scanf("%lld %lld %lld",&aa,&bb,&cc);
a[aa].push_back(End_Dis(bb,cc));
a[bb].push_back(End_Dis(aa,cc));
}
}
void init(ll n){
for(ll i=1;i<=n;i++){
a[i].clear();
}
}
int main(){
while(~scanf("%lld %lld",&n,&m)){
init(n);
read(m);
int ans=Dijkstra(1);
if(ans==INF)puts("-1");
else printf("%lld\n",ans);
}
return 0;
}
当然这道题给我了启示,以前我都是搞懂了Dijkstra算法,但是那个很浅,这个堆优化我相信可以用来解决我前面给出的图的问题:
只需要改一改代码即可:
#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
typedef long long ll;
ll n,m;
struct End_Dis{
ll to,d;//to表示到的点,d表示为前一个点到to这个点的距离
End_Dis(ll a,ll b):to(a),d(b){}///这里构造函数有便于加点
bool operator < (const End_Dis tt) const{//这里在使用优先队列的时候很有用
return d>tt.d;//这个比较特殊,因为优先队列是由大到小,所以我写了一个由大到小的,然后这样会让优先队列由小到大排列(特别的地方)
}
};
vector<End_Dis> a[100000*2];//用邻接表来存储一个点能到的其他点比如:a[aa][i].to表示aa这个点到to这个点
ll book1[200010];//用来标记这个点扫过没有//用来标记这个点是否作为过中转站
ll Dijkstra(ll start){
ll dis[200010];//表示距离
for(ll i=1;i<=n;i++) dis[i]=INF;//先初始化为INF
book1[start]=0;//表示这个点走过了//这里需要注意了 因为这里是和最简单的Dijkstra算法不同点
dis[start]=0;//自己到自己距离为0;
priority_queue<End_Dis> q;//建立一个优先队列
q.push(End_Dis(start,0));//把第一个点放进去
while(!q.empty()) {//循环为非空
End_Dis t=q.top();
q.pop();
if(book1[t.to]) continue;//表示这个点使用过没有
for(ll i=0;i<a[t.to].size();i++){//以这个点位中转站,枚举其他点更新1----其他点的最短距离
End_Dis x=a[t.to][i];//取出t.to这个点所能到达的点的对象
if(dis[x.to]>dis[t.to]+x.d){//start到x.to点的距离 和 start到t.to的距离与t.to到x.d的和的比较
//更新这个点的距离
dis[x.to]=dis[t.to]+x.d;
q.push(End_Dis(x.to,dis[x.to]));//把这个点加入优先队列中
}
}
}
return dis[n];
}
void read(ll m){//因为为无向图
ll aa,bb,cc;
for(ll i=1;i<=m;i++){
scanf("%lld %lld %lld",&aa,&bb,&cc);
a[aa].push_back(End_Dis(bb,cc));
a[bb].push_back(End_Dis(aa,cc));
}
}
void init(ll n){//每次清空
for(ll i=1;i<=n;i++){
a[i].clear();
}
}
int main(){
while(~scanf("%lld %lld",&n,&m)){
init(n);
read(m);
int ans=Dijkstra(1);
if(ans==INF)puts("-1");//如果不能到n点那么久输出-1
else printf("到n点的最短路径为: %lld\n",ans);
}
return 0;
}
这个就是我认为最优的Dijkstra算法版本了(因为这里综合运用了struct+优先队列+巧妙的Dijsktra算法以后就可以直接带模板了,呼,终于整理完了(好像还有保存路径问题(以后遇见我在补充吧)))