【动手学MVG】ICP算法原理和代码实现

介绍

本文介绍了相同尺度的点云ICP算法，若点云之间尺度不同，则需要估计尺度，可以看一下另一篇博文《通过ICP配准两组尺度不同点云, 统一坐标系(附代码)》

本文介绍的ICP问题，是在3D点已配对情况下的ICP，并且，3D点坐标的尺度相同。如果两个点云的尺度不同，需要另外考虑。可以搜索关键字"scale of ICP"。

视觉中的ICP问题描述如下，假设我们有一组配对好的3D点：

$P = \{p_1, ... , p_n\} \\ P' = \{p'_1, ... , p'_n\}$
现在，我们想找一个欧式变换 R, t，使得：
$p'_i = Rp_i+t, 对任意i成立$
这个问题的一种解法（SVD分解的方法）：解耦R和t，先求出R，再代入求得t。

基于SVD的ICP算法

参考论文：K. S. Arun, T. S. Huang and S. D. Blostein, “Least-Squares Fitting of Two 3-D Point Sets,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-9, no. 5, pp. 698-700, Sept. 1987, doi: 10.1109/TPAMI.1987.4767965.

这是1987年提出的方法。

误差函数的构建

首先，假设有 N 组 3D-3D 匹配点对，存在误差 $e_i$ ，则有
$e_i = p'_i - (Rp_i+t)$
构建最小二乘问题，求使误差平方和 $J$ 达到极小的R和t
$\underset{R,t}{min}J = \frac{1}{2}\sum_{i=1}^{N}||e_i||_2^2 = \frac{1}{2}\sum_{i=1}^{N}||p'_i - (Rp_i+t)||_2^2$
**注意：**与平常的单应矩阵、基本矩阵的配对点不同，在3D-3D配对点中，匹配的那一对3D点，其实是空间中同一个点在不同坐标系下的不同表示而已，如下图：

在这里插入图片描述

解耦R和t

首先，引入质心的定义：假设有N个点，每个点的坐标为 $p_i$ ，则质心为
$\boldsymbol{p} = \frac{1}{N}\sum_{i=1}^{N}\boldsymbol{p_i}$

角度一：从几何的角度理解

首先要明确一点：在3D-3D配对点中，匹配的那一对3D点，其实是空间中 同一个点 在不同坐标系下的不同表示而已。

我们可以进行一个坐标变换，移动两个点集的坐标轴，使得两个坐标系的原点重合于各自的质心：
$q_i = p_i - p \\ q'_i = p'_i - p'$
其中， $p$ 和 $p^{'}$ 是各自坐标系下的质心：
$\boldsymbol{p} = \frac{1}{N}\sum_{i=1}^{N}\boldsymbol{p_i} \\ \boldsymbol{p'} = \frac{1}{N}\sum_{i=1}^{N}\boldsymbol{p'_i}$
注意到这两个质心在空间中其实是同一个点。所以坐标变换后的两个点集坐标系原点重合，平移分量t为0，只存在旋转分量。因此误差平方和 $J$ 变为
$\underset{R}{min}J = \frac{1}{2}\sum_{i=1}^{N}||q'_i - Rq_i||_2^2$
这样就实现了R和t的解耦，可以单独对R进行求解（求解R的方法后面再说，先假设已经求得到）。

那么求出R后，怎么求t呢？假设我们所要求得最小二乘解为 $\hat{R}, \hat{t}$ ，记 $p''_i = \hat{R}p_i+\hat{t}$ ，那么 $p'_i$ 和 $p''_i$ 将有相同的质心，即
$p^{'} = p^{''}$
其中，
$\frac{1}{N}\sum_{i=1}^{N}\boldsymbol{p''_i} = \hat{R}p+\hat{t} \\$
所以可以求出t
$\hat{t} = p'' - \hat{R}p = p' - \hat{R}p$

角度二：从数学的角度理解

根据质心的定义，对误差函数进行变换：
$\begin{aligned} \underset{R,t}{min}J &= \frac{1}{2}\sum_{i=1}^{N}||p'_i - (Rp_i+t)||_2^2 \\ &= \frac{1}{2}\sum_{i=1}^{N}||(p'_i - p' - R(p_i - p)) + (p'-Rp-t)||_2^2 \\ &= \frac{1}{2}\sum_{i=1}^{N}(||p'_i - p' - R(p_i - p)||_2^2 + ||p'-Rp-t||_2^2 + 2(p'_i - p' - R(p_i - p))^T(p'-Rp-t)) \\ \end{aligned}$
注意到交叉相部分中 $p'_i - p' - R(p_i - p))$ 在求和之后为零，因此优化目标函数可以简化为
$\begin{aligned} \underset{R,t}{min}J &= \frac{1}{2}\sum_{i=1}^{N}(||p'_i - p' - R(p_i - p)||_2^2 + ||p'-Rp-t||_2^2) \\ &= \frac{1}{2}\sum_{i=1}^{N}(||q'_i - Rq_i||_2^2 + ||p'-Rp-t||_2^2) \\ \end{aligned}$
观察等式右边的左右两项，左边只和旋转矩阵R有关(解耦了t)，而右边既有R也有t。我们先通过左边求解R，再代入右边的部分，另右边部分为零就能得到t。

求解R

前面介绍了怎么解耦R和t，解耦后，只要求得R，就能代入式子直接求得t。下面叙述一下R如何求解，以及为什么可以这么求。

思路是，通过只有R的误差项求解出R。首先展开只有R的误差项：
$\begin{aligned} \frac{1}{2}\sum_{i=1}^{N}||q'_i - Rq_i||_2^2 &= \frac{1}{2}\sum_{i=1}^{N}(q'^T_iq_i + q^T_iR^TRq_i - 2q'^T_iRq_i) \\ &= \frac{1}{2}\sum_{i=1}^{N}(q'^T_iq_i + q^T_iq_i - 2q'^T_iRq_i) \end{aligned}$
注意到前两项都与R无关，因此实际上优化函数变为：
$\sum_{i=1}^{N}-q'^T_iRq_i$
注意到上面式子结果是个1x1的标量的和，所以标量再套个迹的运算，也不影响结果：
$\begin{aligned} \sum_{i=1}^{N}-q'^T_iRq_i &= \sum_{i=1}^{N}tr(-q'^T_iRq_i) \\ &= -\sum_{i=1}^{N}tr(q'^T_i(Rq_i)) \\ &= -\sum_{i=1}^{N}tr((Rq_i)q'^T_i) \\ &= -\sum_{i=1}^{N}tr(R(q_iq'^T_i)) \\ &= -tr(R\sum_{i=1}^{N}q_iq'^T_i) \\ \end{aligned}$
上面的推导用到了迹的性质，详情看附录。

为了求解R，定义矩阵W：
$\sum_{i=1}^{N}q_iq'^T_i$
W是一个3x3的矩阵，对其进行SVD分解，有
$W = UDV^T$
令 $X = VU^T$ ，这里不考虑它是怎么想到的，但可以证明它是使得误差函数最小的最小二乘解。

证明 $X = VU^T$ 是最小二乘解

将 $R = X = VU^T$ 代入误差函数，取代R那一项，有
$\begin{aligned} -tr(R\sum_{i=1}^{N}q_iq'^T_i) &= -tr(RW) \\ &= -tr(XW) \\ &= -tr(VU^TUDV^T) \\ \end{aligned}$
由于V和U都是正交矩阵，所以 $U^TU = E$ ，则上式变为
$tr(VDV^T)$
因为 $VDV^T$ 是一个对称正定矩阵，所以可以推断 $X W$ 是一个对称正定矩阵。

由附录中的辅助定理1，对于任意正交矩阵B，和对称正定矩阵 $X W$ ，我们有
$\ge tr(BXW)$
所以取 $X = VU^T$ 时， $t r (B X W)$ 取得最大值，也就是 $- t r (B X W)$ 取得最小值。但是， $- t r (B X W)$ 取得最小值，与我们要求的误差函数 $- t r (R W)$ 取最小值有什么关系呢？

可以看一下，B和X都是正交矩阵，而B是一个任意的正交矩阵，所以BX可以表示任意的正交矩阵。这表明了我们在所有正交矩阵中，找到了一个解 $VU^T$ 使得误差函数最小，那这个解也能使得 $- t r (R W)$ 取最小值。我们只需要进一步判断这个解是不是旋转矩阵即可。

判断X是否为所需的解

上面已经说了， X 是最小二乘解，它使得误差函数最小。但是由于噪声和匹配点共线的原因，X 不一定是一个旋转矩阵，也就是说不一定是我们需要的解。

接下来分析其什么时候 X 是我们所需的解，什么时候不是，如果不是的时候，能不能通过它找到我们所需的解（我们需要的解必须要是一个旋转矩阵）。简要的说明如下，如果需要详细说明请看论文：

$q_i$ 不共面。 此时另误差函数取最小值的X，必定是旋转矩阵。
- **特殊情况： $q_i$ 不共面，但 $d e t (x) = - 1$ ，即得到的解是个反射矩阵。**这种情况发生在噪声特别大的情况下，此时没有旋转矩阵能比反射矩阵使得误差更小。这种情况下不能用最小二乘法求解该问题，考虑使用RANSAC方法。
$q_i$ 共面，但不共线。 当W的奇异值有且仅有一个为0时， $q_i$ 共面。此时有两个解都能使得误差函数取最小，分别是一个旋转矩阵和一个反射矩阵。
- 此时改变 $v_3$ (W奇异值分解后V矩阵的第3列向量) 的正负号不会改变W的值，但是却能使得X从反射矩阵变为旋转矩阵，或者从旋转矩阵变为反射矩阵.
- 所以当 $d e t (x) = - 1$ 时(反射矩阵的行列式为-1)，通过改变 $v_3$ 的正负号，使得X变为我们所需要的旋转矩阵。
$q_i$ 共线。 当且仅当有两个奇异值相等时， $q_i$ 共线。此时有无穷多的旋转矩阵和反射矩阵X，都能使误差函数最小，这种情况下用最小二乘法可能不能求解该问题，考虑使用RANSAC方法。

总的来说就是，当 $d e t (x) = + 1$ 时，得到的就是所需的解；反之当 $d e t (x) = - 1$ 时，只有点共面的情况下，我们能通过修改结果得到解，其他情况下都不行，考虑用RANSAC方法。

在大部分情况下，这就是ICP的解。具体证明见下一小节，这里先分三种情况简要说明：

$q_i$ 不共面。只有旋转矩阵X能使得误差为0

其中D是奇异值组成的对角阵，并且奇异值按照从上到下，按照从大到小排列。

下面求解R，分三种情况：

第一种：无噪声情况
- $q_i$ 不共面。只有旋转矩阵X能使得误差为0
- qi共面，但不共线。有一个旋转矩阵X和一个反射矩阵X能使得误差为0，但是很容易验证。具体咋弄？
  - 对H进行SVD分解 H = UDV^T ，当且仅当只有一个奇异值为0时，这些点共面。
  - 此时改变v_3的正负号不会改变H的值，但是却能使得X从反射矩阵变为旋转矩阵，或者从旋转矩阵变为反射矩阵
  - 所以当det(x)=-1时（反射矩阵），通过改变v_3的正负号，使得X变为我们需要的旋转矩阵。
- qi共线。有无穷多的旋转矩阵和反射矩阵X，能使得误差为0. 这种情况时，该方法解不了。
  - 当且仅当有两个奇异值相等时，这些点共线。
第二种：有噪声情况
- s
- qi共面，结论和无噪声的一样，只是误差不能为0了，只是取最小。特殊的情况是只有3对匹配点的情况
- 不能处理的情况是：解X为反射矩阵(det(X)=-1) ，且H没有奇异值为0的情况（即点qi不共面）。此时没有旋转矩阵能比反射矩阵使得误差更小，这种情况一般只发生在噪声特别大的情况下，此时用最小二乘解可能始终得不到正确答案。这时候用RANSAC之类的方法剔除外点可能更好（一次只用3个点计算ICP）。

$R=UV^T$ 还是 $VU^T$ ?

如果同时看过《视觉slam十四讲》和论文 “Least-Squares Fitting of Two 3-D Point Sets” ，你可能会产生一个困惑：在论文中， $R=VU^T$ ，但在书《视觉slam十四讲》中， $R=UV^T$ ，他们的公式并不相同，这是因为在推导过程中对W的定义不同导致的。

在论文中，推导用的相关公式如下：
$\begin{aligned} p'_i &= Rp_i + T + N_i \\ W &= \sum_{i=1}^{N}q_iq'^T_{i} \\ R &= VU^T \\ \end{aligned}$
在书《视觉slam十四讲》中，推导用的相关公式如下：
$\begin{aligned} p_i &= Rp'_i + t + e_i \\ W &= \sum_{i=1}^{N}q_iq'^T_{i} \\ R &= UV^T \\ \end{aligned}$
可以看到，它们的旋转矩阵R，一个是从 $p_i$ 到 $p'_i$ 的，另一个正好相反，但是W的矩阵定义却是一样的，这就是差异所在。实际上，书《视觉slam十四讲》中的定义不够直观，它的W应该定义为 $\sum_{i=1}^{N}q_iq'^T_{i}$ 的转置才更合适，正是由于它们对W的定义差了一个转置，所以导致得到的解R，也差一个转置( $UV^T=(VU^T)^T$ )。

算法流程总结

求两组点的质心 $p, p^{'}$

$\boldsymbol{p} = \frac{1}{N}\sum_{i=1}^{N}\boldsymbol{p_i} \\ \boldsymbol{p'} = \frac{1}{N}\sum_{i=1}^{N}\boldsymbol{p'_i}$

得到两组点的去质心坐标

$q_i = p_i - p \\ q'_i = p'_i - p'$

计算矩阵W

$\sum_{i=1}^{N}q_iq'^T_i$

对W进行SVD分解，得到可能的解 $X = VU^T$

$W = UDV^T \\ X = VU^T$

判断X是否为所需解

如果 $d e t (X) = + 1$ ， X是一个旋转矩阵，即为所需的解。

如果 $d e t (X) = - 1$ ， X是一个反射矩阵。

如果W有且仅有一个奇异值为0，那么所需的旋转矩阵解为
$X' = V'U^T$
其中， $V^{'} = [v 1, v 2, - v 3]$ ，即把V的最后一列向量符号取反。

如果W没有奇异值为0，那么用最小二乘的方法解不出来，改用RANSAC方法求解ICP问题。

若计算得到了所需的解R = X，代入公式求得t

$t = p^{'} - R p$

至此，R和t都已经求出来了。

代码实现

下面摘自《视觉SLAM十四讲》第七章。（这应该是本书第二版的代码，因为第一版代码中并没有判断解X是否为反射矩阵）

void pose_estimation_3d3d (
    const vector<Point3f>& pts1,
    const vector<Point3f>& pts2,
    Mat& R, Mat& t
)
{
    
    
    Point3f p1, p2;     // center of mass
    int N = pts1.size();
    for ( int i=0; i<N; i++ )
    {
    
    
        p1 += pts1[i];
        p2 += pts2[i];
    }
    p1 = Point3f( Vec3f(p1) /  N);
    p2 = Point3f( Vec3f(p2) / N);
    vector<Point3f>     q1 ( N ), q2 ( N ); // remove the center
    for ( int i=0; i<N; i++ )
    {
    
    
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }

    // compute q1*q2^T
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for ( int i=0; i<N; i++ )
    {
    
    
        W += Eigen::Vector3d ( q1[i].x, q1[i].y, q1[i].z ) * Eigen::Vector3d ( q2[i].x, q2[i].y, q2[i].z ).transpose();
    }
    cout<<"W="<<W<<endl;

    // SVD on W
    Eigen::JacobiSVD<Eigen::Matrix3d> svd ( W, Eigen::ComputeFullU|Eigen::ComputeFullV );
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();
    
    if (U.determinant() * V.determinant() < 0)
	{
    
    
        for (int x = 0; x < 3; ++x)
        {
    
    
            U(x, 2) *= -1;
        }
	}
    
    cout<<"U="<<U<<endl;
    cout<<"V="<<V<<endl;

    Eigen::Matrix3d R_ = U* ( V.transpose() );
    Eigen::Vector3d t_ = Eigen::Vector3d ( p1.x, p1.y, p1.z ) - R_ * Eigen::Vector3d ( p2.x, p2.y, p2.z );

    // convert to cv::Mat
    R = ( Mat_<double> ( 3,3 ) <<
          R_ ( 0,0 ), R_ ( 0,1 ), R_ ( 0,2 ),
          R_ ( 1,0 ), R_ ( 1,1 ), R_ ( 1,2 ),
          R_ ( 2,0 ), R_ ( 2,1 ), R_ ( 2,2 )
        );
    t = ( Mat_<double> ( 3,1 ) << t_ ( 0,0 ), t_ ( 1,0 ), t_ ( 2,0 ) );
}

附录

矩阵的迹

参考：百度百科-矩阵的迹

在线性代数中，一个n×n矩阵A的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵A的迹（或迹数），一般记作 tr(A)。

性质：

迹是所有对角元素的和
迹是所有特征值的和
tr(AB)=tr(BA)
$t r (m A + n B) = m * t r (A) + n * t r (B)$

Lemma 1（辅助定理 1）

《Least-Squares Fitting of Two 3-D Point Sets》中使用的一个辅助定理。

对于任何正定矩阵 $AA^T$ 和任何正交矩阵B(orthonormal)，有
$tr(AA^T) \ge tr(BAA^T)$

证明：
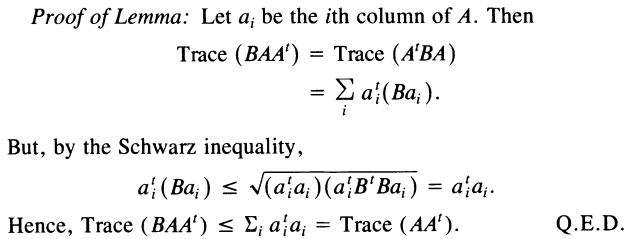
在这里插入图片描述

$AA^T$ 和 $A^TA$ 的性质

参考：https://blog.csdn.net/Europe233/article/details/86720864

对于任意一个矩阵 $A\in R^{m×n}$ ，则 $AA^T$ 和 $A^TA$ 都是对称半正定矩阵。

证明：

$AA^T$ 显然对称，同时有： $x∈R^n,x^TA^TAx=(Ax)^T(Ax)≥0$

同理可证 $A^TA$ 对称半正定.

正交矩阵的性质

两个正交矩阵的积也是正交矩阵
任意正交矩阵的行列式只有两种取值：+1和-1

参考文献

《视觉SLAM十四讲》第一版 - 高翔
K. S. Arun, T. S. Huang and S. D. Blostein, “Least-Squares Fitting of Two 3-D Point Sets,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-9, no. 5, pp. 698-700, Sept. 1987, doi: 10.1109/TPAMI.1987.4767965.

利用SVD分解求ICP问题的方法，看了十四讲后再看这个就容易很多。如果还看不懂可以先看看下面的参考链接“多视图几何之SVD”。
多视图几何之SVD | 证明了多个问题下为何能用SVD求解 | ICP中为何SVD可行 | 8点法求基本矩阵求解，为何是用SVD的最后一列向量 | 本质矩阵恢复R和t为什么可以用SVD | SVD为什么能求最小二乘解
$AA^T$ 和 $A^TA$ 的性质