继续拿最长回文子串开练,话不多说,先来看O(n^2)的中心枚举法~

因为回文串是中心对称的,所以我们可以先枚举中心,然后枚举长度,尝试向两边扩展。
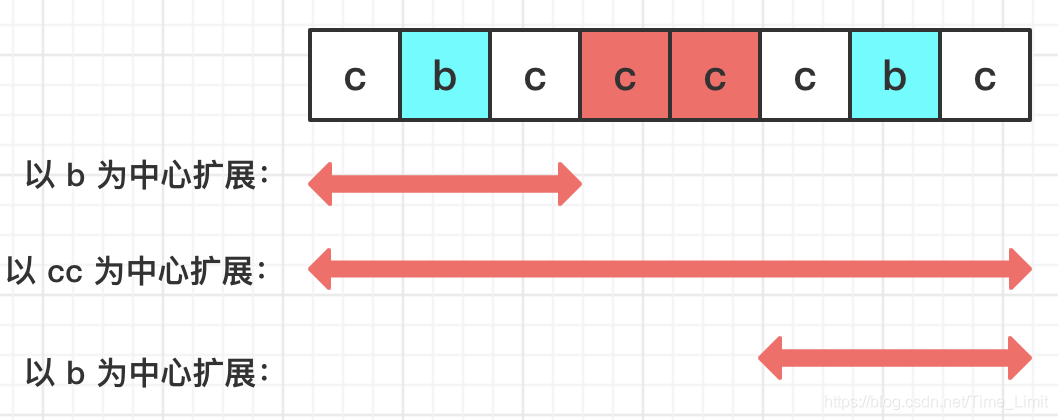
需要注意回文串的长度,如果是奇数的话,中心是一个字符,如果是偶数的话,中心是两个字符,比如上图中的"cc"就是最长字符的中心。
string longestPalindrome(string s) {
int pos = 0, len = s.size() ? 1 : 0;
for(int i = 0; i < s.size(); i++) {
int l = i, r = i; // 以 s[i] 中心,向两边扩展
while(0 <= l && r < s.size() && s[l] == s[r]) {
l--;
r++;
}
if(r-l-1 > len) {
len = r-l-1;
pos = l+1;
}
l = i, r = i+1; // 以 s[i],s[i+1] 为中心,向两边扩展
while(0 <= l && r < s.size() && s[l] == s[r]) {
l--;
r++;
}
if(r-l-1 > len) {
len = r-l-1;
pos = l+1;
}
}
return s.substr(pos, len);
}
机智的老铁们,有没有从上图中发现一些端倪?两个 “b” 是关于 “cc” 对称的,且都包含在以"bb"为中心的回文子串中,那就意味着当已知以左"b"为中心的回文长度时,以右"b"为中心的回文长度就不用从0开始探测了。
这就是 Manacher 算法的精髓!充分利用已知的回文串,减少不必要的校验,使得时间复杂度降至O(n)!

马拉车第一步,插入占位符
选择一个原字符串中不存在的字符作为占位符,将占位符插入到原字符串的 n+1 个间隔。比如字符串"abba",变为"$a$b$b$a$"。这使得所有回文子串的长度都变成了奇数!
这可以用反证法证明一下:如果一个回文子串的长度是偶数,那么必然一端是占位符,另一端不是占位符,这与回文串的定义是矛盾的!

马拉车第二步,初始化
s :原始的字符串。
str : s 插入占位符之后得到的字符串。
L :算法过程中,已知的右端点最靠右的,回文子串的,左端点,初始为 0。
R :算法过程中,已知的右端点最靠右的,回文子串的,右端点,初始为 -1。
dp :一个数组。dp[i] 表示以 str[i] 为中心的回文子串的长度。
马拉车第三步,计算dp数组!
- 从 0 开始枚举 i :
- 如果 i 不在 [L,R] 中,dp[i] = 1。仅含一个字符的子串肯定是回文的。
- 如果 i 在 [L,R] 中,那么由对称的特性可知,dp[i] = min((R-i)*2-1, dp[L+R-i])。
- 使用中心枚举法探测更长的子串,从 dp[i] 开始探测长度。
- dp[i]确定后,若 i+dp[i]/2 > R,说明找到了右端点更靠右的子串,那么更新L,R:
- L = i - dp[i]/2
- R = i + dp[i]/2
- 遍历 dp,找到最大的 dp[i],根据 i 及 dp[i] 可以计算出 str 中最长回文子串的左右端点,然后可以计算出原始字符串 s 中最长回文子串的左右端点。
我觉得可以这样理解马拉车算法:从中心枚举法的基础上,加了一个 dp 数组,利用回文串中心对称的特性,加速了探测长度的过程。
dp 数组是如何工作的
接下来,再理解一下 dp数组是如何工作的。

可以发现,因为整个字符串都是回文的,使得 dp 数组也是中心对称的!这也就是意味着,当求出前一半时,后一半可以直接利用中心对称的特性直接获得!回文子串对应的 dp 子数组都是中心对称的吗?很遗憾,并不是,比如下图:
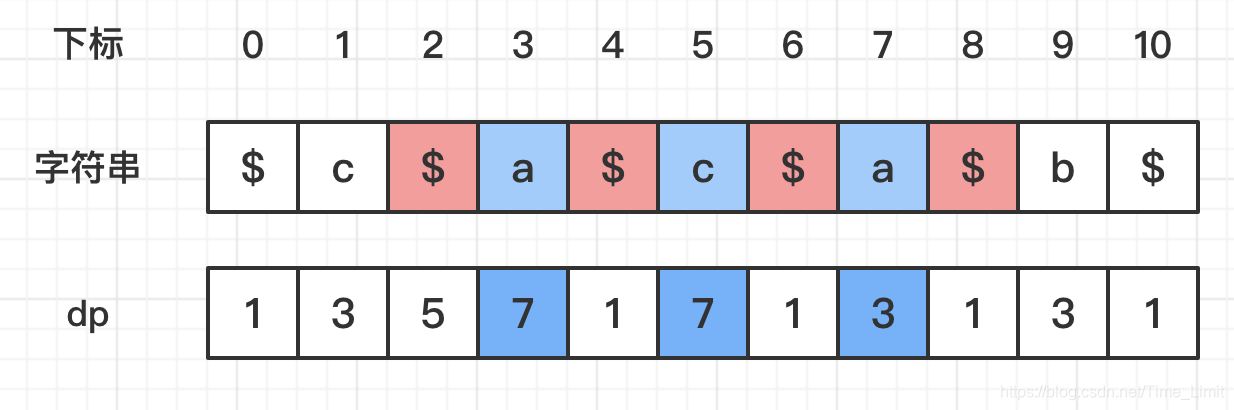
图中的 S[2:8] 构成了一个回文子串,然而 dp[2:8] 子数组并不是中心对称的。
既然这样,我们在利用回文子串 S[L:R] 计算 dp[i] 时,需要注意边界问题:设 dis 为 i 到 R 的距离,i_mirror 为与 i 中心对称的下标,
- S[L:R] 得出的 dp[i] 不能超过 dis*2+1。如果超过了该值,那 dp[i] 代表的子串就超出了 S[L:R] 的范围,那 dp[i] 的有效性就无法保证了。
- 同时,由中心对称得出的 dp[i] 也不能比 dp[i_mirror] 更大。如果超过了,也无法保证 dp[i] 的有效性了。
综上所述:
- 当 i 被一个回文串S[L:R]覆盖时,可以加速 dp[i] 的探测过程:
- dp[i] = min((R-i)*2+1, dp[R+L-i])
- 当 i 没有被回文串覆盖时:
- dp[i] = 1
这也解释了,探测过程中要保存右端点最靠右的串而不是最长的回文子串的原因:因为我们是从左到右枚举的,这样可以最大程度的覆盖还没有计算的 dp,这样才能更有效的加速!
还要明白一点:上述公式只是加速了 dp 的探测,而不是直接得到最优解。所以,加速之后,我们还要继续探测。
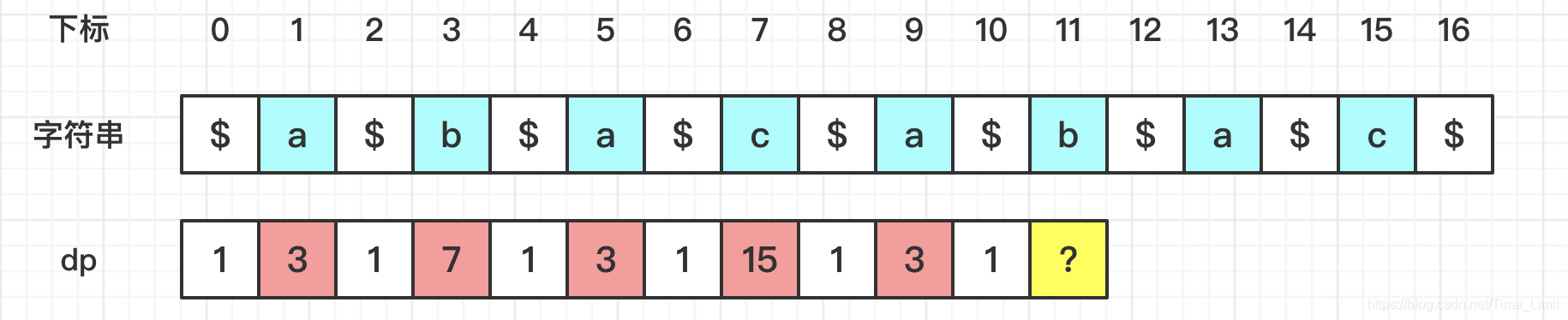
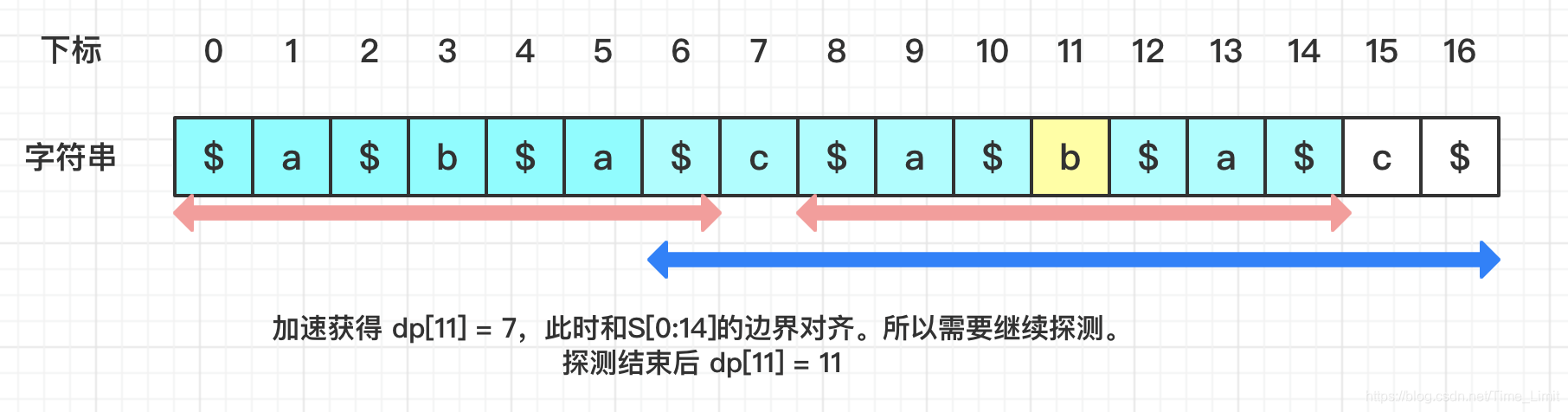
当要计算 dp[11] 时,如按中心枚举法,需从 1 开始探测。但马拉车加速后,可以直接从 7 开始:
- 已知的最右回文串为 S[0:14],则 (14-11)*2+1 = 7。
- i_mirror = R+L-i = 14+0-11 = 3,则 dp[3] = 7。
- 所以dp[11] = min(7,7) = 7。
然后继续探测,发现了以 S[11] 为中心的更长的回文子串 S[6:16],其长度为 11。
Manacher算法只是对中心枚举法的优化!!只是利用了回文串的中心对称特性!!只是加速了长度的探测过程!!

时间复杂度
接下来,尝试证明一下Manacher算法的时间复杂度。
当开始计算 dp[i] 时:
- 如果 i <= R,则可以进行加速,加速之后 dp[i] 标识的回文子串 P[i] 的右端点有两种情况:
- P[i] 的右端点等于 R。此时需要继续探测。
- P[i] 的右端点小于 R。此时不需要继续探测了,因为P[i] 完全内含在了 S[L:R] 中,不可能继续扩张了。
- 如果 R < i,则 dp[i] 要从 1 开始探测。
下列图片展示了未覆盖,内含,边界对齐三种情况:
- 未覆盖
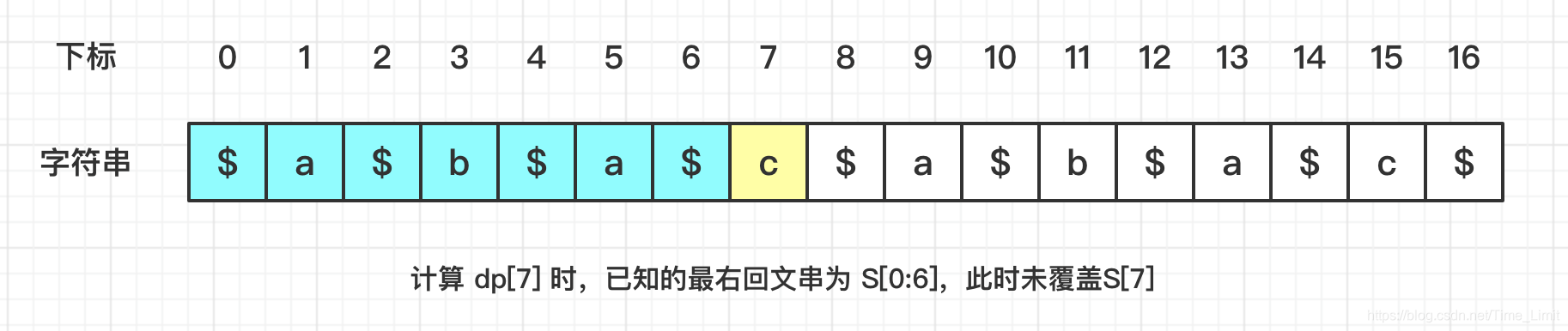
- 内含

- 边界对齐
可以发现,当 dp[i] 内含于S[L:R]时,则计算过程结束,时间复杂度O(1)。
其他情况下,则需要继续探测。如果探测成功,则会更新R,这是因为只有 R 之后的字符才会被探测。如果探测失败,则计算过程结束。
也就是说,每个字符最多会被成功探测一次,每个dp[i]最多会探测失败一次。即平均每个字符最多会有一次成功探测和一次失败探测。
所以总的时间复杂度为O(n)。
每次证明时间复杂度都感觉语无伦次

string Manacher(const string &s) {
string str;
int n = s.size();
str.resize(n*2+1);
// 占位符使用'\0'。
for(int i = 0, j = 0; i < n; i++) {
str[j++] = 0;
str[j++] = s[i];
}
//初始化数据
n = s.size()*2+1;
str[n-1] = 0;
vector<int> dp;
dp.resize(n);
//计算dp
int L = 0, R = -1;
for(int i = 0; i < n; i++) {
if(i <= R) {
// i 被[L,R] 覆盖了
int limit = ((R-i)<<1)-1;
dp[i] = min(limit, dp[L+R-i]);
if(dp[i] < limit) { // 内含。探测结束
continue;
}
} else {
dp[i] = 1; // 未被覆盖。从 1 开始迭代。
}
//开始中心枚举法中的探测长度的步骤
int halfLen = dp[i]>>1;
int l = i - halfLen - 1, r = i + halfLen + 1;
while(0 <= l && r < n && str[l] == str[r]) {
--l;
++r;
}
//尝试更新dp[i] 及 L,R
dp[i] = r-l-1;
if(r > R) {
R = r-1;
L = l+1;
}
}
// 找到最长的回文子串的位置与长度。
int len = 0, pos = 0;
for(int i = 0; i < n; i++) {
if(dp[i] > len) {
len = dp[i];
pos = i;
}
}
// 映射到原始字符串中的位置。
return s.substr(pos/2 - len/4, len/2);
}
画大饼
现在已经学会了解决回文串的利器Manacher算法。下一次我会和大家分享刷题中的实战经验~
