Day9：蒙特卡洛法（求圆周率）

Day9：蒙特卡洛法（求圆周率）

一. 问题背景：

在只有一个随机数生成器的情况下如何估计π的大小？

二. 解决思路：

蒙特卡洛法：

    蒙特卡洛方法又称统计模拟法，随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法。是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名

    早在17世纪，人么就知道用事件发生的“频率”来决定事件的“概率”。这也是蒙特卡洛法的基本思想。当样本数量足够大时，我们可以用频率去估计概率。这也是求圆周率π的常用方法。

                                                                        

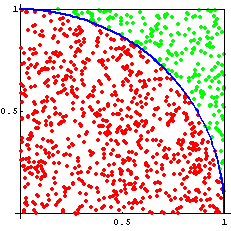
    当我们在（0，1）的范围内随机选择一个坐标（x, y）时，每个坐标点被选中的概率相等。则坐标落在直径为1的正方形中的圆的概率为：

                                                                       （均匀分布）

                                                                     

    由切比雪夫不等式可知，在生成大量随机点的前提下我们能得到尽可能接近圆周率的值。

三. 算法实现：

#1
from random import random
from time import perf_counter
DARTS = 1000*1000
hits = 0.0
start = perf_counter()
for i in range(1, DARTS+1):
    x, y = random(), random()  #random()返回随机生成的一个实数，它在[0,1)范围内。
    dist = x ** 2 + y ** 2     #等价于dist = pow(x ** 2 + y ** 2, 0.5)
    if dist <= 1.0:
        hits = hits + 1
pi = 4 * (hits/DARTS)
print("圆周率值是: {}".format(pi))
print("运行时间是: {:.5f}s".format(perf_counter() - start))



#2
import numpy as np
from time import perf_counter
def pi(n, batch=1000):
    t = 0
    for i in range(n // batch):
        ### 随机获取坐标（batch个点）
        p = np.random.rand(batch, 2)   #以给定的形状创建一个数组，并在数组中加入在[0,1]之间均匀分布的随机样本。
        ### 计算坐标平方和
        p = (p * p).sum(axis=1)        #数组元素对位相乘,最外围axis=0
        ### 平方和小于1的即为落在圆中的点
        t += (p <= 1).sum()
    return 4 * t / n

start = perf_counter()
Pi = pi(10 ** 8)
print(Pi)
print("运行时间是: {:.5f}s".format(perf_counter() - start))

 

注：numpy 数组和矩阵的乘法的理解    https://blog.csdn.net/bbbeoy/article/details/72576863