区间调度问题（贪心算法与动态规划）

问题描述

给定n个活动，其中的每个活动ai包含一个起始时间si与结束时间fi。设计与实现算法从n个活动中找出一个最大的相互兼容的活动子集S。
要求：分别设计动态规划与贪心算法求解该问题。其中，对贪心算法分别给出递归与迭代两个版本的实现。

问题分析

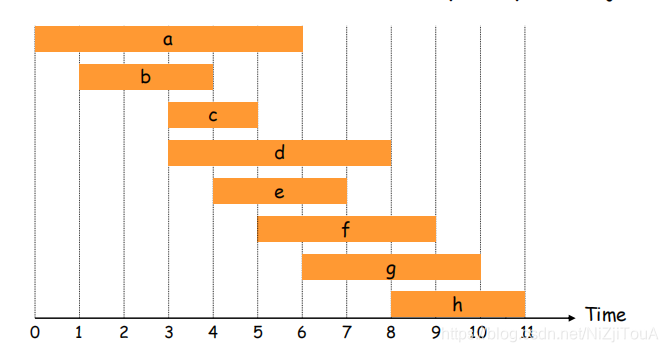
对于上述问题，可简化为上方图片，当上一个活动结束后，才可以进行下一个活动，对同一时间线来讲，如上图，从0-11，a与g满足题意，由于a还未结束，b就开始，所以a与b不满足题意。

算法分析

要寻找最大互相兼容子集S，显然要确定每一个活动的开始时间与结束时间。即需要确定活动的次序，我们以活动结束时间作为标准对活动进行排序。如下例：

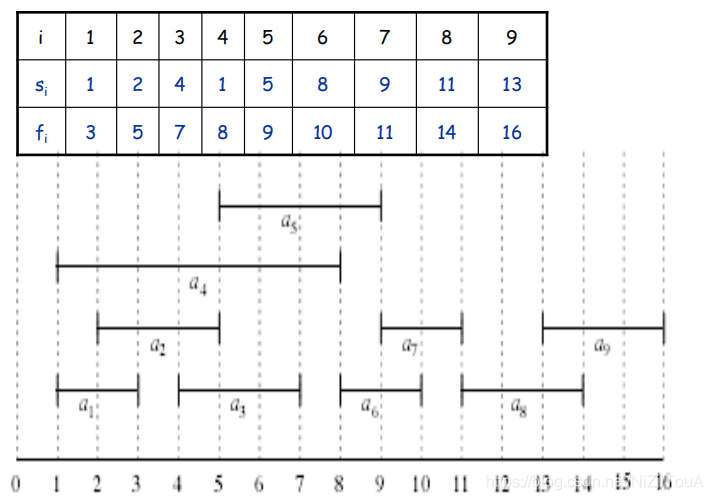
显然，可以得到两个最大兼容子集。

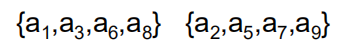
动态规划

首先我们用动态规划的思想来解决上述问题。
1、定义子问题：我们定义Sij满足存在ak使得fi<=sk<=fk<=sj，形象来讲就是存在ak活动使得它在ai结束之后,aj开始之前。即

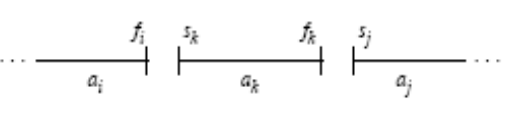
那么整个问题该怎么去描述呢，活动1到活动n若表示为 s1n显然并不包含活动1与活动n，这里我们就增加两个虚活动分别在两端，即S0=0，Sn+1=∞。
2、建立DP方程：定义完子问题，建立DP方程就相对简单，显然Sij=Sik+ak+Skj。

3、求解DP方程：首先要寻找到符合兼容子集的k值，自然就对i到j之间所有的k值遍历一遍就可以。

int Dp(vector<int>S, vector<int>E)
{
	int n = S.size();
	int **C = new int*[n];
	for (int i = 0; i < n; i++)
		C[i] = new int[n];
	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
			C[i][j] = 0;
	for(int j=0;j<n;j++)
		for (int i = 0; i < n; i++)
		{
			if (i < j)
			{
				for(int k=i+1;k<j;k++)
					if (S[k] >= E[i] && E[k] <= S[j])
					{
						if (C[i][j] < C[i][j] + C[k][j] + 1)
							C[i][j] = C[i][j] + C[k][j] + 1;
					}
			}
		}
/*	for (int i = 0; i < n; i++)
		for (int j = 0; j < n; j++)
		{
			cout << C[i][j] << " ";
			if (j == n - 1)
				cout << endl;
		}*/
	return C[0][n - 1];
}

可见动态规划算法的时间复杂度为O（n^3）

贪心算法

贪心算法较为简单，这里就不过多赘述。
递归实现：

void recursive(vector<int> S, vector<int> E, int i, int j)
{
	int m = i + 1;
	while (m <= j&&S[m] < E[i])
		m = m + 1;
	if (m <= j)
	{
		cout << m << " ";
		recursive(S, E, m, j);
	}
}

迭代实现：

void iterative(vector<int>S, vector<int>E)
{	
	vector<int>A = { 1 };
	int i = 1;
	for (int m = 2; m < S.size()-1; m++)
	{
		if (S[m] > E[i])
		{
			A.push_back(m);
			i = m;
		}
	}
	for (int i = 0; i < A.size(); i++)
		cout << A[i] << " ";
}