题目:
经过激烈的争夺,Lele终于把那块地从Yueyue的手里抢了回来。接下来,Lele要开始建造他的灌溉系统。
通过咨询Lele的好友——化学系的TT,Lele决定在田里挖出N条沟渠,每条沟渠输送一种肥料。
每条沟渠可以看作是一条折线,也就是一系列线段首尾连接而成(除了第一条线段开头和最后一条线段的结尾)。由于沟渠很细,你可以忽略掉它的宽度。
由于不同的肥料之间混合会发生化学反应,所以修建的沟渠与沟渠之间不能相交。
现在TT给Lele画了一些设计图,Lele请你判断一下设计图中的沟渠与沟渠之间是否有相交。
Input
本题目包含多组测试,请处理到文件结束(EOF)。
每组测试的第一行有一个正整数N(0<N<30),表示管道的数目。接下来给出这N条管道的信息。
对于每条管道,第一行是一个正整数K(0<K<100),表示这条管道是由K个端点组成。
接下来的K行给出这K个端点信息。每个端点占一行,用两个整数X和Y(0<X,Y<1000)分别表示这个端点的横坐标和纵坐标的值。
Output
对于每组测试,如果该测试管道与管道之间有相交的话,输出"Yes",否则输出"No"。
Sample Input
2
2
0 0
1 1
2
0 1
1 0
2
2
0 0
1 1
2
1 0
2 1
2
3
0 0
1 1
2 1
2
2 0
3 0
Sample Output
Yes
No
No
分析:
外积,又称叉积,是向量代数(解析几何)中的一个概念。两个向量v1(x1, y1)和v2(x2, y2)的外积v1×v2=x1y2-y1x2。如果由v1到v2是顺时针转动,外积为负,反之为正,为0表示二者方向相同(平行)。此外,文中涉及行例式和方程组的概念,请参阅线性代数的相关内容。
那如何来判断两线段是否相交呢?
假设有两条线段AB,CD,若AB,CD相交,我们可以确定:
1.线段AB与CD所在的直线相交,即点A和点B分别在直线CD的两边;
2.线段CD与AB所在的直线相交,即点C和点D分别在直线AB的两边;
上面两个条件同时满足是两线段相交的充要条件,所以我们只需要证明点A和点B分别在直线CD的两边,点C和点D分别在直线AB的两边,这样便可以证明线段AB与CD相交了。
那判断两线段是否相交与一开始提到的向量叉乘定理有什么关系呢?有,我们可以通过叉乘来证明上面说的充要条件。看下图:
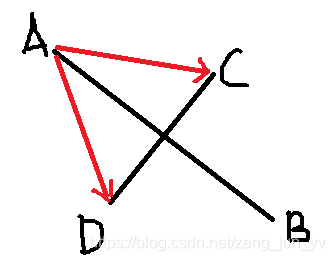
在上图中,线段AB与线段CD相交,于是我们可以得到两个向量AC,AD,C和D分别在AB的两边,向量AC在向量AB的逆势针方向,AB×AC > 0;向量AD在向量AB的顺势针方向,AB×AD < 0,两叉乘结果异号。
这样,方法就出来了:如果线段CD的两个端点C和D,与另一条线段的一个端点(A或B,只能是其中一个)连成的向量,与向量AB做叉乘,若结果异号,表示C和D分别在直线AB的两边,若结果同号,则表示CD两点都在AB的一边,则肯定不相交。
当然,不能只证明C,D在直线AB的两边,还要用相同的方法证明A,B在直线CD的两边,两者同时满足才是线段相交的充要条件。
不过,线段相交还有一些特殊情况:
1.只有1点相交,如下图:
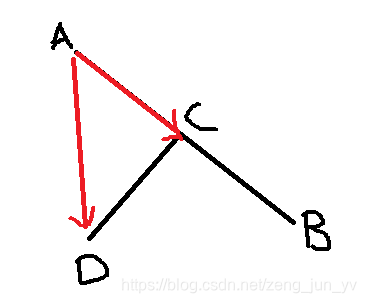
上图中,线段AB与CD相交于C点,按照之前介绍的方法,我们可以连成两向量AD和AC,这时候,我们发现,AC与AB共线,AB×AC = 0;而AB×AD < 0;两者并不异号,可实际上仍然相交。所以当出现两叉乘结果中,有一方为0,也可以看成点CD在直线AB的两边。
2.两条线段重合,如下图:

在上图中,线段AB与线段CD重合,重合部分为CB,这种重合的情况要特殊判断:
首先,我们给没条线段的两个端点排序,大小判断方法如下:横坐标大的点更大,横坐标相同,纵坐标大的点更大。
排好序后,每条线段中,小的点当起点,大的当终点。我们计算向量AB×向量CD,若结果为0,表示线段AB平行CD,平行才有了重合的可能;但平行也分共线和不共线,只有共线才有可能重合,看下图:
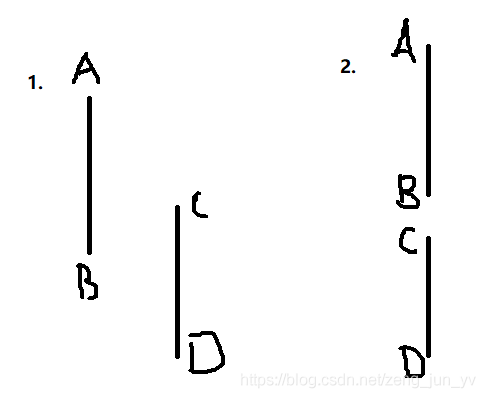
上图中,第一种情况不共线,第二种情况共线。那如何来判断是否共线呢?
我们可以在两条线段中各取一点,用这两点组成的向量与其中一条线段进行叉乘,结果若为0,就表示两线段共线,如下图:
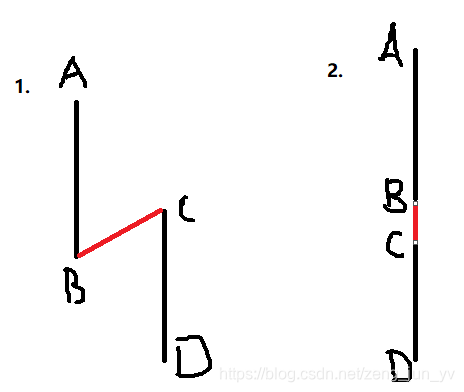
我们取向量BC,若BC×CD = 0,表示两点共线,即是第二种情况,否则就是第一种情况。第一种情况肯定不相交。然而,即使他们共线,却还是不一定重合,就如上图中第二种情况。这时候,之前给点排序的妙处就体现出来了:
若一条线段AB与另一条线段CD共线,且线段AB的起点小于等于线段CD的起点,但线段AB的终点(注意是终点)大于等于线段CD的起点(注意是起点),或者交换一下顺序,CD的起点小于AB的起点…只要满足其中一个,就表示有重合部分。
为方便计算,对坐标点的大小比较作如下定义:x坐标较大的点为大,x坐标相等但y坐标较大的为大,x与y都相等的点相等。一条线段中较小的一端为起点,较大的一端为终点。
两条线段的位置关系大体上可以分为三类:有重合部分、无重合部分但有交点(相交)、无交点。为避免精度问题,首先要将所有存在重合的情况排除。重合可分为:完全重合、一端重合、部分重合三种情况。显然,两条线段的起止点都相同即为完全重合;只有起点相同或只有终点相同的为一端重合(注意:坐标较小的一条线段的终点与坐标较大的一条线段的起点相同时应判定为相交)。要判断是否部分重合,必须先判断是否平行。设线段L1(p1->p2)和L2(p3->p4),其中p1(x1,
y1)为第一条线段的起点,p2(x2, y2)为第一条线段的终点,p3(x3, y3)为第二条线段的起点,p4(x4,
y4)为第二段线段的终点,由此可构造两个向量:v1(x2-x1, y2-y1),v2(x4-x3, y4-y3)
若v1与v2的外积v1×v2为0,则两条线段平行,有可能存在部分重合。再判断两条平行线段是否共线,方法是用L1的一端和L2的一端构成向量vs并与v2作外积,如果vs与v2也平行则两线段共线(三点共线)。在共线的前提下,若起点较小的线段终点大于起点较大的线段起点,则判定为部分重合。没有重合,就要判定两条线是否相交,主要的算法还是依靠外积。然而外积的计算开销比较大,如果不相交的情况比较多,可先做快速排斥实验:将两条线段视为两个矩形的对角线,并构造出这两个矩形。如果这两个矩形没有重叠部分(x坐标相离或y坐标相离)即可判定为不相交。
然后执行跨立试验。两条相交的线段必然相互跨立,简单的讲就是p1和p2两点位于L2的两侧且p3和p4两点位于L1的两侧,这样就可利用外积做出判断了。分别构造向量s1(p3,
p1), s2(p3,
p2),如果s1×v2与s2×v2异号(s1->v2与s2->v2转动的方向相反),则说明p1和p2位于L2的两侧。同理可判定p3和p4是否跨立L1。如果上述四个叉积中任何一个等于0,则说明一条线段的端点在另一条线上。当判定两条线段相交后,就可以进行交点的求解了。当然,求交点可以用平面几何方法,列点斜式方程来完成。但这样作会难以处理斜率为0的特殊情况,且运算中会出现多次除法,很难保证精度。这里将使用向量法求解。
设交点为(x0, y0),则下列方程组必然成立:
x0-x1=k1(x2-x1) y0-y1=k1(y2-y1) x0-x3=k2(x4-x3) y0-y3=k2(y4-y3)
其中k1和k2为任意不为0的常数(若为0,则说明有重合的端点,这种情况在上面已经被排除了)。1式与2式联系,3式与4式联立,消去k1和k2可得:x0(y2-y1)-x1(y2-y1)=y0(x2-x1)-y1(x2-x1)
x0(y4-y3)-x3(y4-y3)=y0(x4-x3)-y3(x4-x3) 将含有未知数x0和y0的项移到左边,常数项移动到右边,得:(y2-y1)x0+(x1-x2)y0=(y2-y1)x1+(x1-x2)y1
(y4-y3)x0+(x3-x4)y0=(y4-y3)x3+(x3-x4)y3 设两个常数项分别为b1和b2:b1=(y2-y1)x1+(x1-x2)y1 b2=(y4-y3)x3+(x3-x4)y3
系数行列式为D,用b1和b2替换x0的系数所得系数行列式为D1,替换y0的系数所得系数行列式为D2,则有:|D|=(x2-x1)(y4-y3)-(x4-x3)(y2-y1) |D1|=b2(x2-x1)-b1(x4-x3)
|D2|=b2(y2-y1)-b1(y4-y3) 由此,可求得交点坐标为:x0=|D1|/|D|, y0=|D2|/|D| 解毕。
AC代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int n,flag;
int k[40];
struct node
{
int x,y;
} s[40][110];
double f(node a,node b,node c)///如果AB.AC,得到的结果是垂直于ABC这个平面的一个向量
{///两个向量的向量积,是一个垂直于两个向量的向量
return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);///AB.AC=(b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
}
int dfs(node a,node b,node c,node d)
{
if(max(a.x,b.x)>=min(c.x,d.x)&&max(c.x,d.x)>=min(a.x,b.x)&&
max(a.y,b.y)>=min(c.y,d.y)&&max(c.y,d.y)>=min(a.y,b.y)&&
f(a,b,c)*f(a,d,b)>=0/**(ABxAC)*(ADxAB)>=0,就是说明这
两个向量积的方向相同,也就是姆指方向相同,也就是两个线段相交的判
断条件。*/&&f(a,c,d)*f(b,d,c)>=0)
return 1;///如果AB和CD相交,可以画个图看看,ABxAC和ADxAB的拇指方向是相同的,ACxAD和BDxBC的拇指方向也是相同的。
return 0;
}
int main()
{
while(~scanf("%d",&n))
{
memset(k,0,sizeof(k));
flag=0;
for(int i=0; i<n; i++)
{
scanf("%d",&k[i]);
for(int j=0; j<k[i]; j++)
scanf("%d%d",&s[i][j].x,&s[i][j].y);
}
if(n==1)
{
printf("No\n");
continue;
}
for(int i=0; i<n-1; i++)///枚举
for(int j=1; j<k[i]; j++)
for(int u=i+1; u<n; u++)
for(int v=1; v<k[u]; v++)
if(dfs(s[i][j-1],s[i][j],s[u][v-1],s[u][v]))
{
flag=1;
break;
}
if(flag)
printf("Yes\n");
else
printf("No\n");
}
return 0;
}