Codeforces Round #645 (Div. 2) Solution

前言

终于橙名了.(我应该是最水的橙名了,QAQ~~)

$A$

签到题.

$B$

签到题+1.
一拨人一起冲进去一定不会不优!
枚举那个阈值即可.

int n,a[N];
 
 
int main() {
	int _;qr(_); while(_--) {
		qr(n);for(int i=1;i<=n;i++) qr(a[i]);
		sort(a+1,a+n+1);
		int ans=0;
		for(int i=1;i<=n;i++) if(i>=a[i]) ans=max(ans,i);
		pr2(ans+1);
	}
	return 0;
}

$C$

考场上想了一个比较麻烦的做法.

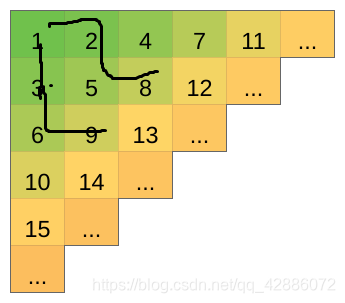
由上图可观察到,从一个格子出发向右和向下后相似的路径中,下面那部分每个格子的值都比上面对应位置要大1.

由于总共有 $x2-x1+y2-y1$次移动,所以等价于预处理一个该长度的01串作为差分数组( $x2-x1个1$)),我们求得前缀和后,每个位置的权值和就是和最小路径和的差.
我们求得最大路径与最小路径的差即可.

关于为啥期间每个值都出现:只要移动路径中存在 $7$字形线路(先横后下),(即不是最大值),那么我们可以调整为先下后上,这样明显权值+1.证毕!

ps:比赛时候好像把x,y搞反了,但是没有啥问题.

int main() {
	int _;qr(_); while(_--) {
		ll a,b,c,d,u,v,w; qr(a);qr(b); qr(c); qr(d);
		u=d-b; v=c-a; w=u+v; 
		pr2((w+v+1)*u/2-(u+1)*u/2+1);
	}
	return 0;
}
 

官方题解:由上面的调整权值和的做法可以看出,路径每次把一个格子下移,所以总共的下移次数为 $(x2-x1)*(y2-y1)$,即除去最小路径上的点的总点数.
代码更显然:

int T;
ll a,b,c,d;

int main() {
	qr(T); while(T--) {
		qr(a); qr(b); qr(c); qr(d);
		pr2((c-a)*(d-b)+1); 
	}
	return 0;
}

$D$

复制一遍,暴力扫描即可.

ll n,x,d[N],c[N],ans;
 
int main() {
//	int _;qr(_); while(_--) {
		qr(n); qr(x); for(int i=1;i<=n;i++) qr(d[i]),d[i+n]=d[i];
		for(int i=1;i<=2*n;i++) c[i]=c[i-1]+(d[i]+1)*d[i]/2,d[i]+=d[i-1];
		ans=x;
		for(int i=1,j=0;i<=2*n;i++) {
			while(d[i]-d[j]>x) j++;//(j,i]为整月.
			ll y=d[j]-d[j-1],t=min(y,x-(d[i]-d[j]));
			ans=max(ans,c[i]-c[j]+(y+y-t+1)*t/2);
		}
		pr2(ans);
//	}
	return 0;
}
 

$E$

如果 $k\le \dfrac n 2,$那么 $2k$也一定合法.( $s[i+k]-s[i]>0,s[i+2k]-s[i]>0\rightarrow s[i+2k]-s[i]>0$)

所以,我们只需考虑 $k\in [\lceil \dfrac n 2 \rceil,n]$的情况即可.(spj,比赛的时候好像并没有注意到这点)

定义 $s_i=\sum_{j=i}^{i+k-1} a_j,初始时k=\lceil \dfrac n 2 \rceil.$
当我们把 $k+1$时, $\Delta s_i=a_{i+k}=x,$与此同时,合法的 $s$下标的上界-1( $n-k+1->n-k$).

我们只需维护一个 $s$的前缀最小值即可快速判断 $k$是否合法.

int n,t,a[N];
ll m[N],s,x;

int main() {
	qr(n); t=(n+1)/2;
	for(int i=1;i<=t;i++) qr(a[i]);
	qr(x);
	for(int i=1;i<=n-t;i++) {
		s+=x-a[i];
		m[i]=min(m[i-1],s);
	}
	s=0;
	for(int i=1;i<=t;i++) s+=a[i];
	for(int i=t;i<=n;i++) {
		if(s+m[n-i]>0) return pr2(i),0;
		s+=x;
	}
	return puts("-1"),0;
}

$F$

考虑逆向考虑问题,
操作分别为:

• 差分b
• 翻转b

由于连续翻转,所以差分的次数可以用于计算复杂度.
为了最大化差分的次数,我们再次使用逆向思维.
最多能进行多少次对初始长度为 $n$且全为 $1$的数组进行前缀和.

$t<\sqrt[n-1]{C\cdot (n-1)!},C=10^{25}$
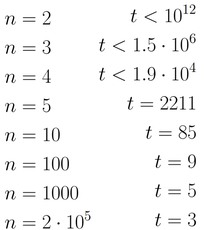
这个需要用到不等式的缩放.
首先如果做 $t$次前缀和,那么第 $i$个位置对第 $n$个位置的贡献等价于 $从(1,i)->(t,n)每次只能向右或向下走的方案数.$
最后第 $n$项为 $\sum_{i=1}^n C_{t-i+n-1}^{t-1}=C_{n+t-1}^t=\dfrac{(n+t-1)!}{t!(n-1)!}$(画个杨辉三角即可证明).
$\dfrac{(n+t-1)!}{t!(n-1)!}>\dfrac{t^{n-1}}{(n-1)!}=C$.
我们解右边的方程的 $t$显然比实际大.

也就是说: $n>2$时, $n\cdot ans$是在可接受范围内,所以直接枚举即可.
否则, $n=2$时,用类似欧几里得的方法求解即可.

int n,flag=0;
ll a[N],b[N];

ll s1,s2,c[N*10];
char s[N*10];int top;
void push(char ch,ll t=1) {s[++top]=ch; c[top]=t; s1+=t; if(ch=='P') s2+=t;}

int calc(ll *a) {// 判断上升/下降/都不满足
	int x=1,y=2;
	for(int i=1;i<n;i++) 
		x&=(a[i-1]>a[i]),
		y&=(a[i-1]<a[i])*2;
	return x|y;
}
void fz(ll *a) {reverse(a,a+n);}
bool pd() {
	for(int i=0;i<n;i++) 
		if(a[i]^b[i]) return 0;
	return 1;
}

int main() {
	qr(n); 
	for(int i=0;i<n;i++) qr(a[i]);
	for(int i=0;i<n;i++) qr(b[i]);
	if(n==1) {
		if(a[0]==b[0]) puts("SMALL\n0");
		else puts("IMPOSSIBLE");
		return 0;
	}
	else if(n==2) {
		flag=(a[0]>a[1]);
		if(flag) swap(a[0],a[1]);
		if(b[0]>b[1]) push('R'),swap(b[0],b[1]);
		while(b[0]>a[0]) {
			ll t=b[1]%b[0];
			push('P',b[1]/b[0]);
			push('R');
			b[1]=b[0]; b[0]=t;
		}
		if(b[0]^a[0]) return puts("IMPOSSIBLE"),0;
		else {
			if(b[1]>=a[1]&&(b[1]-a[1])%a[0]==0) push('P',(b[1]-a[1])/a[0]);
			else return puts("IMPOSSIBLE"),0;
		}
		if(flag) push('R',1);
	}
	else {
		flag=calc(a);
		if(flag==1) fz(a);
		int t;
		while(t=calc(b)) {
			if(t==1) push('R'),fz(b),t=1;
			if(pd()) {t=-1; break;}
			for(int i=n-1; i;i--) b[i]-=b[i-1];
			push('P');
		} 
		if(t^(-1)) {
			if(pd()) t=-1;
			else {
				fz(b); push('R');
				if(pd()) t=-1;
			}
		}
		if(t==-1) {
			if(flag==1) push('R');
		}
		else return puts("IMPOSSIBLE"),0;
	}
	if(s2>2e5) puts("BIG"),pr2(s2);
	else {
		puts("SMALL");
		pr2(s1);
		while(top) {
			int k=c[top];
			while(k--) putchar(s[top]);
			top--;
		}
	}
	return 0;
}