冲激响应与卷积

该系列为DR_CAN工程数学基础系列视频笔记，详见https://space.bilibili.com/230105574
由于笔者水平有限，文中难免存在一些不足和错误之处，诚请各位批评指正。

1 卷积定义

函数 \(f,g\) 是定义在 \(R^{n}\)上的可测函数（measurable function）， \(f,g\) 的卷积记作\(f * g\)，它是其中一个函数翻转，并平移后，与另一个函数的乘积的积分，是一个对平移量的函数，也就是：

\[(f * g)(t) \stackrel{\text { def }}{=} \int_{\mathbb{R}^{n}} f(\tau) g(t-\tau) d \tau \]

如果函数不是定义在 \(R^{n}\)上，可以把函数定义域以外的值都规定成零，这样就变成一个定义在 \(R^{n}\)上的函数。

2 冲激响应定义

在信号处理中，冲激响应（英语：Impulse response）一般是指系统在输入为单位脉冲函数时的输出（响应），是暂态响应中的一种。对于连续时间系统来说，脉冲响应一般用函数 \(h(t,\tau)\) 来表示，相对应的输入信号，也就是单位脉冲函数满足狄拉克δ函数的形式，其函数定义如下：

\[\delta(t)=0, t \neq 0\\\int_{-\infty}^{\infty} \delta(t) d t=1 \]

在输入为狄拉克δ函数时，系统的脉冲响应 \(h(t)\) 包含了系统的所有信息。所以对于任意输入信号 \(x(t)\) ，可以用连续域卷积的方法得出所对应的输出 \(y(t)\) 。也就是：

\[y(t)=\int_{-\infty}^{\infty} x(\tau) h(t-\tau) d \tau=x(t) * h(t) \]

对于离散时间系统来说，脉冲响应一般用序列 \(h[n]\) 来表示，相对应的离散输入信号，也就是单位脉冲函数满足克罗内克δ的形式，在信号与系统科学中可以定义函数如下：

\[\delta[n]=\left\{\begin{array}{ll} 1, & n=0 \\ 0, & n \neq 0 \end{array}\right. \]

同样道理，在输入为 \(\delta[n]\) 时，离散系统的脉冲响应 \(h[n]\) 包含了系统的所有信息。所以对于任意输入信号 \(x[n]\) ，可以用离散域卷积（求和）的方法得出所对应的输出信号 \(y[n]\) 。也就是：

\[y[n]=\sum_{k=0}^{\infty} x[k] h[n-k] \]

3 线性非时变系统

4 弹簧阻尼系统的例子

对于一个线性系统来说，他的输出相应 \(x(t)\) 就等于输入 \(f(t)\) 与其传递函数 \(H(s)\) 经过拉普拉斯逆变换后得到的冲激响应 \(h(t)\) 的卷积：

我们将输入信号的一段离散分成三个 \(\Delta T\) ，这三个部分分别会对系统产生作用，并且作用之间相互独立，即产生对应的相互独立的输入响应，也就是输出。而某一时刻 \(t\) 系统的输出，即为 \(t\) 时刻前各输入响应的加和，当 \(\Delta T \rightarrow 0\) 时，这个加和就变成了积分：

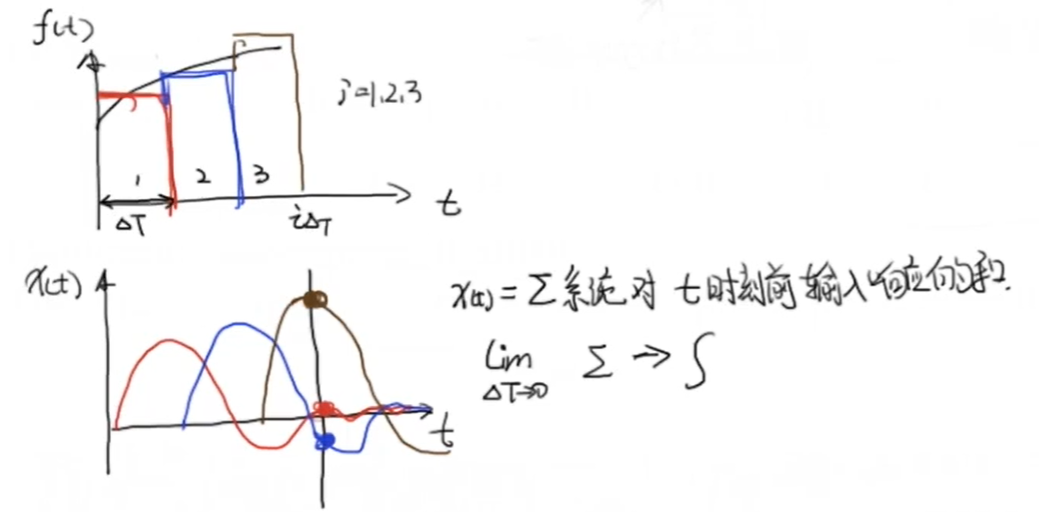
同样的，当 \(\Delta T \rightarrow 0\) 时， \(t\) 时刻的这一小段输入就可以近似为冲激函数的 \(f(t)\) 倍。根据线性非时变系统的性质，我们可以得到这个输入与输出的表格：

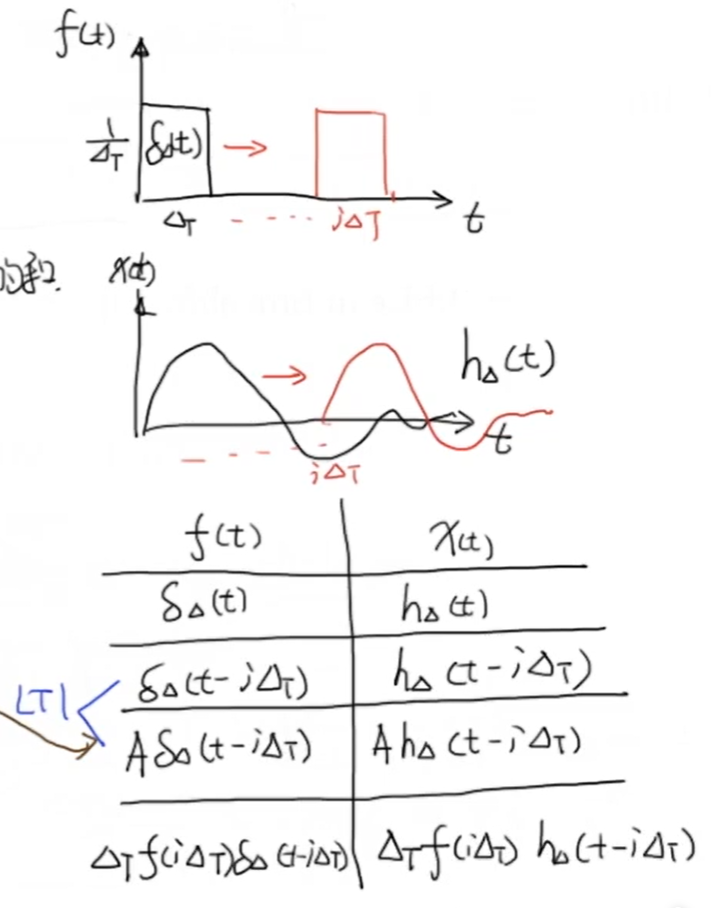
其中第一行即为一个冲击产生的影响，可以理解为一个基本形式

第二行表示这个冲击延后 \(i\Delta T\) 时间后，输入响应也将延后 \(i\Delta T\)

第三行则意味着冲激强度（图像面积）为 \(A\) 时，并且延后 \(i\Delta T\) 后，系统的输入响应将为基本形式延后 \(i\Delta T\) 的 \(A\) 倍

第四行即为第三行的推广，通过把 \(A\) 替换成输入函数在 \(i\Delta T\) 时刻下， \(\Delta T\) 小段的面积。他表示这个系统对一个面积为 \(\Delta T f(i\Delta T)\) 的冲击输入在延迟 \(i\Delta T\) 之后的输入响应

根据叠加原理，我们可以将这个时刻以前所有的输入都加在一起，这样就得到了这一时刻系统的响应。就可以写成：

\[ x(t)=\sum_{i=0}^{j} \Delta T f\left(i \Delta T\right) h_{0}(t-i \Delta T) \quad t=j \Delta T \]

当 \(\Delta T \rightarrow 0\) 时， \(i\Delta T = \tau\) ，上式就可以写成卷积的形式：

\[x(t)=\int_{-\infty}^{\infty} f(\tau) h(t-\tau) d \tau=f(t) * h(t) \]

5 启发

通过以上分析，我们可以发现，对于线性非时变系统，冲激响应 \(h(t)\) 可以完全定义系统。这也就是我们把传递函数表示为 \(H(s)\) 的原因，即冲激响应 \(h(t)\) 经过拉普拉斯变换后得到传递函数 \(H(s)\) 。