D. Count the Arrays(组合数学+卢卡斯定理)

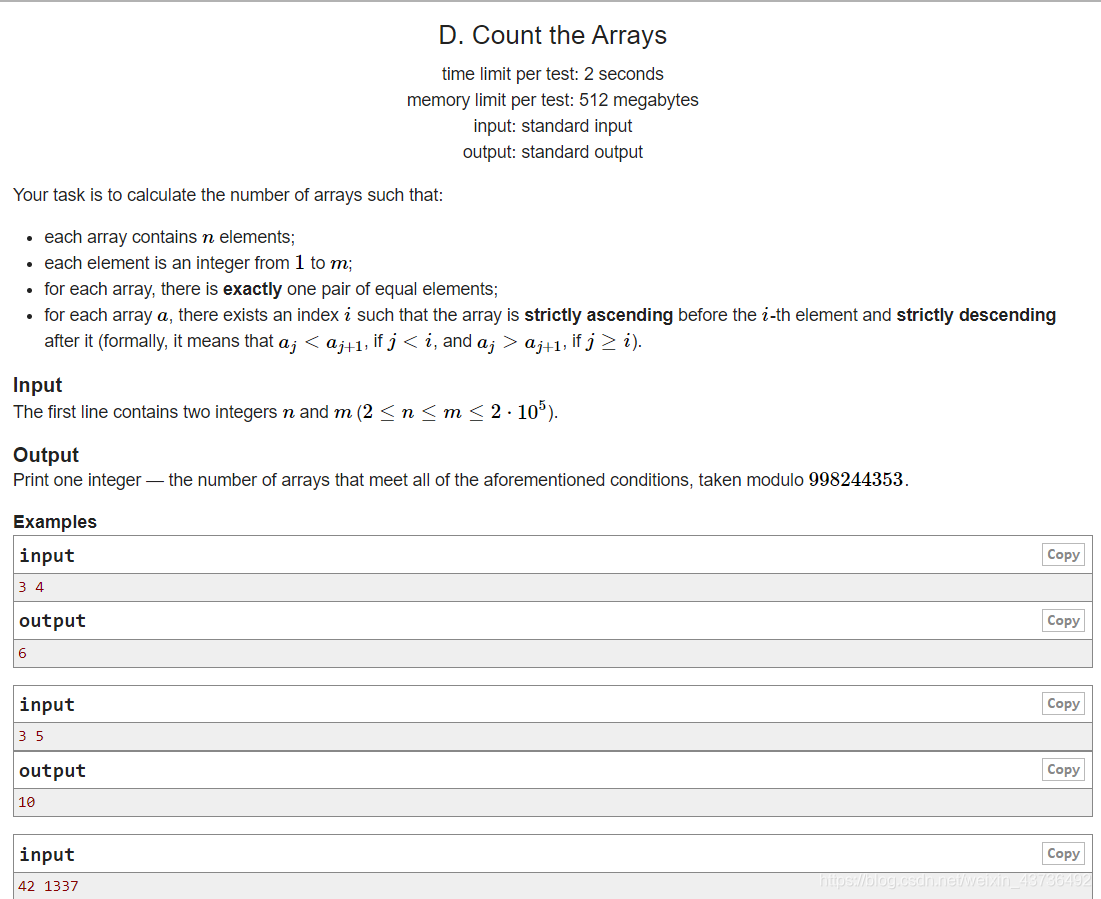
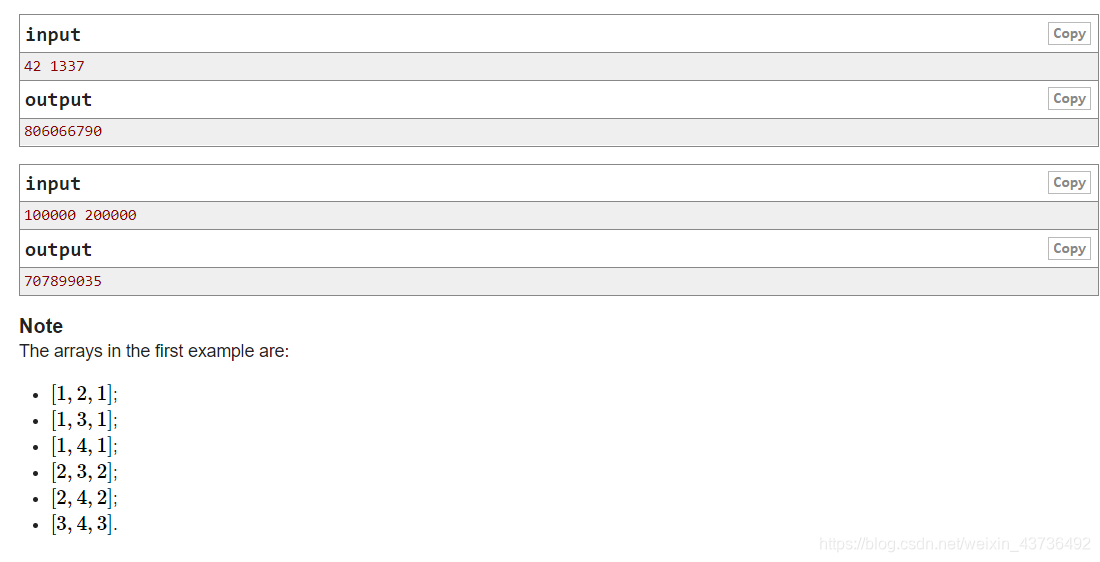
题目大意：
给你一个长度为n的数列，然后让你用[1,m]这些数填在数列里面。(n<=m)
满足：
数列里面有n个数
元素值的取值范围[1,m]
存在一对相同的元素
先是单调递增然后单调递减。

思路：
先在m个元素选n-1个放到数列中并且满足单调递增，选取的种数 = C(m,n-1)(找了好久的组合数符号都没找到)，然后还剩下一个位置，这时将我们只需要固定n-1这个位置是最大值，然后从左边的n-2中任取一个数放到第n个位置依旧满足条件，那么这个时候的答案 = C(m,n-1) * (n-2).
我们考虑的是第n-1个位置是最大值但是最大值也有可能是(n-2)中位置的某一个，要得到这种情况，我们只需要把前面n-3(即固定最大值和最大值左右两边相同的数让他继续满足单增然后单减)，这时我们可以将最大值右边n-3个数移动到第n个数后面仍旧满足条件，可以移动0个，一个，两个。。。或者n-3个保证数列长度不变，这样就得到了最大值在前面的所有情况。这样的取值一共有 2 ^ ( n - 3 ) 种。
最后答案 = ( n - 2 ) * C ( m , n - 1 ) * ( 2 ^ ( n - 3 ) )
由于最后要对mod取模，组合数取模要用到卢卡斯定理(虽然我不懂，但是我有板子)。
代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long int ll;
const ll mod = 998244353 ;
ll f[200010];
ll fastpow(ll a,ll b){
	ll ans = 1;
	while(b>0){
		if(b&1)ans = ans * a % mod;
		a = a * a % mod ;b >>= 1;
	}
	return ans;
}
ll c(int x,int y){
	return f[x]*fastpow(f[y],mod-2)%mod*fastpow(f[x-y],mod-2)%mod;
}
int main(){
	ll n,m;
	cin>>n>>m;
	f[0]=1;
	for(int i=1;i<=m;i++)f[i]=f[i-1]*i%mod;
	if(n == 2)cout<<"0"<<endl;
	else{
		cout<<(n-2)*c(m,n-1)%mod*fastpow(2,n-3)%mod<<endl;
	}
}