这是我之前在剑桥大学上的一节研究生应数选修课 Image Reconstruction,之前没怎么听懂,所以这段时间想把它补起来。
这节课老师没有明确的讲义,所以我就照记着的一些书的顺序,把它复习了。
整堂课只有我一个人上 QAQ,所以应该算是在数学系里比较小众的方向吧。
因此这篇笔记 基本上是为了 我自己以后查资料或公式好找一点。
笔记部分摘自 Mathematical Methods in Image Reconstruction. F.Natterer and F.Wuebbeling.
引言
图像重构 Intro
Radon Transform 拉东变换
Rf
-
拉东变换是一个积分变换
-
先它将定义在二维平面上的一个函数
f(x1,x2) 沿着平面上的任意一条直线做线积分,相当于对函数
f(x1,x2) 做 CT扫描
-
令 X射线 在
x 点 线性衰减后 为
f(x)。 那么 X射线光束
L 经过的部分成像就是
g(L)=∫Lf(x)dx 。
-
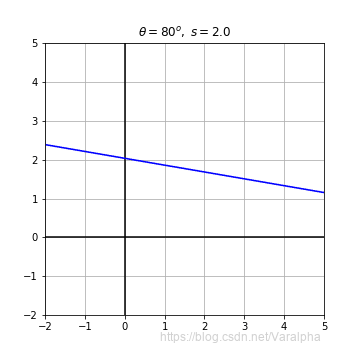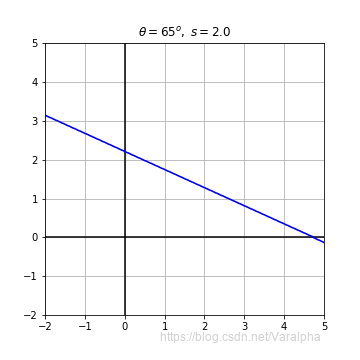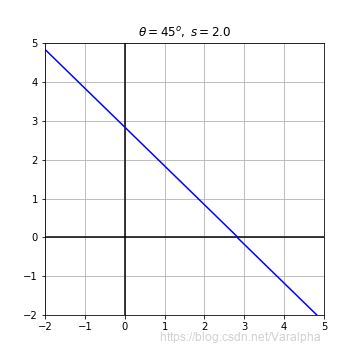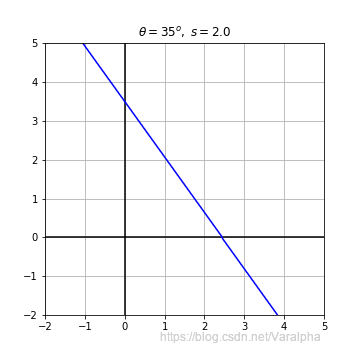
如果我们用
s (原点到射线的距离)与
θ (距离的夹角)表示射线
L, 如图:
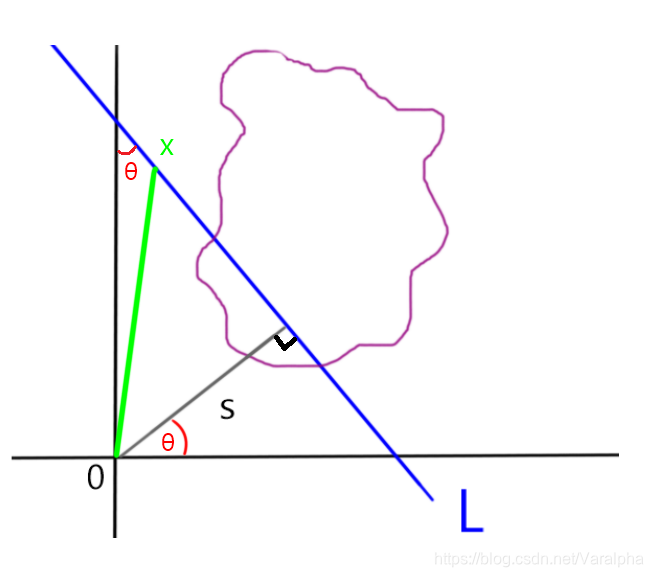
-
可得这条直线为
L(θ,s)={x∈R2:x⋅θ=s},θ∈S1,s∈R1
-
可得如下方程:
g(θ,s)=∫x⋅θ=sf(x)dx=(Rf)(θ,s)
import matplotlib.pyplot as plt
import numpy as np
x1 = np.arange(-10,10.01,.01)
x2 = np.arange(-10,10.01,.01)
xv = np.meshgrid(x1,x2)
degree = 45
theta = degree/180 *np.pi
s = 2.
Lv = abs(xv[0]*np.cos(theta) + xv[1]*np.sin(theta)-s)
L = np.max((Lv<0.01)*xv[1],axis=0)+np.min((Lv<0.01)*xv[1],axis=0)
plt.plot(x1[L.nonzero()],L[L.nonzero()],'blue')
plt.show()
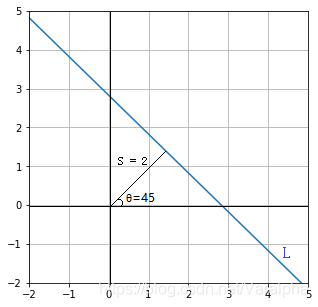
- 我还做了变量为
s 和
θ 的动图:
- 接下来,把它拓展到更高维度 n 维。
- 构筑 n 维超平面
H(θ,s)={x∈Rn:x⋅θ=s},θ∈Sn−1 (unit sphere) ,s∈R1
- 超平面垂直于
θ 距离为
s
- 同时
H(−θ,−s)=H(θ,s) 为 偶函数
- 可定义
(Rf)(θ,s)=∫x⋅θ=sf(x)dx=∫H(θ,s)f(x)dx
-
Rf 函数在 单位圆柱 unit sylinder 上
Cn={(θ,s):θ∈Sn−1,s∈R1}
-
因为
H(−θ,−s)=H(θ,s) , 所以
(Rf)(−θ,−s)=Rf(θ,s) 为偶函数
-
由于
s−x⋅θ=0 变换可得:
(Rf)(θ,s)=∫Rnδ(s−x⋅θ)f(x)dx
-
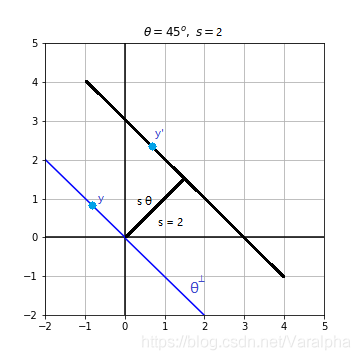
θ⊥={x∈Rn:x⋅θ=0} 正交
θ 的子空间
(Rf)(θ,s)=∫θ⊥f(sθ+y)dy
- 由于
f∈S(Rn) 在速降函数空间内(Schwartz space)
- 那么
Rf∈S(Cn)
-
S(Cn) 为
S(Cn)={g∈C∞(Cn):sl∂sk∂kg(θ,s) bounded ,l,k=0,1,⋯}
(g⋆h)(θ,s)=∫R1g(θ,s−t)h(θ,t)dt
傅里叶变换
F
F(g(θ,s))=(2π)−1/2∫R1g(θ,s)e−isσds
- 当
f∈S(Rn),θ∈Sn−1 (unit sphere) ,σ∈R1
F[(Rf)(θ,σ)]Cn=(2π)2n−1F[f(σθ)]Rn
- 当
f,g∈S(Rn)
CnRf⋆Rg=RnR(f⋆g)
BackProjection operator 后向投影 算子
R∗
(R∗g)(x)=∫Sn−1g(θ,x⋅θ)dθ,g∈S(Cn)
-
因此 对于
g=Rf,(R∗g)(x) 是 所有超平面 经过
x,
f 的积分 的均值。
-
在数学中 可以说
R∗ 是
R 的共轭
-
对于
g∈S(R1),f∈S(Rn)
∫R1g(s)(Rf)(θ,s)ds=∫Rng(x⋅θ)f(x)dx
- 对于
g∈S(Cn),f∈S(Rn)
∫Sn−1∫R1gRfdθds=∫Rn(R∗g)f(x)d(x)dx
- 当
f∈S(Rn) 和
g∈S(Cn)
(R∗g)⋆f=R∗(g⋆Rf)
- 当
g∈S(Cn) 为偶 (例
g(θ,s)=g(−θ,−s) )
F[(R∗g)(ξ)]=2(2π)2n−1∣ξ∣1−nF[g(∣ξ∣ξ,∣ξ∣)]
- 通过 Riesz potential 里斯位势 在
Cn
F[(Iαg)(θ,σ)]=∣σ∣−αF[g(θ,σ)],α<1





