目录
1 功能
最小二乘法是基于大量带有误差的数据估计真值的算法。首先要注意,使用这个算法,首先要满足一个条件:大量,如果测量数据和要估计的真值形成一对一的关系,那显然估计是毫无意义的。测量数据必须相对于带估计的数值是“冗余”的。举个例子,你用直尺测量绳子的长度,只量一次,那么你测多少就是多少,只有你测试次数的足够多,获得的数据才可以用最小二乘法估计真值。
最小二乘法,为什么叫“最小二乘”?实际上,“二乘”的意思就是“平方”,也即是“最小平方法”。什么的最小平方呢,当然是误差的最小平方啦。
2 公式推导
我们从最简单的说起:量长度,我们对一个绳子的长度测了好几次,第i次的长度计为
![]()
设 为估计值,那么误差
的表达式就是:
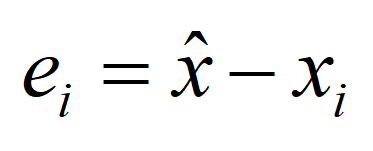
误差的平方 可以写成:
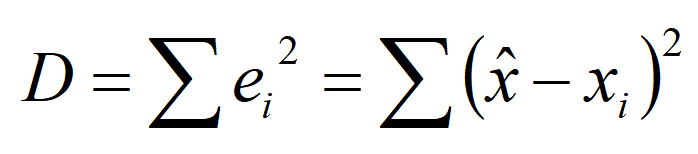
要让误差的平方 最小,也就是求这个函数的最小极值,求导就行:
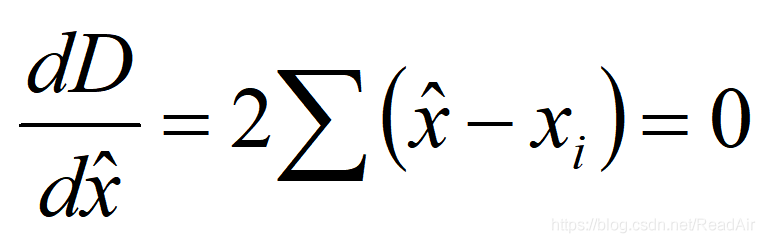
根据上式可得:
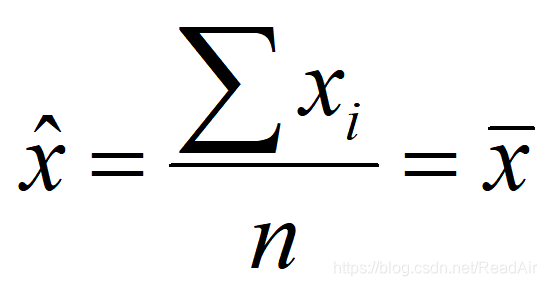
一看这公式,恍然大悟,原来就是取平均值啊。真没想到求算术平均竟然也是最小二乘法的应用呢!
上面是找的是长度,说白了是在找 (a为常数) ,下面来说一个复杂的:
![]()
我们现在手上有大把的 ,如何估计出
和
呢?
首先构造误差的平方 :
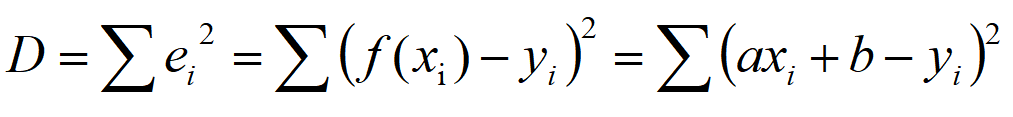
这次有俩参数,要求偏导为0:
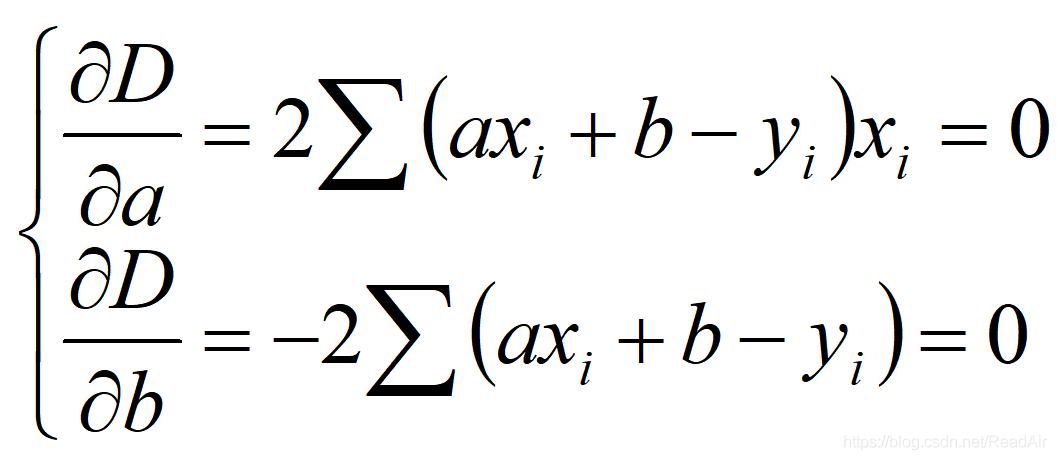
由D对b的偏导分析得到:
![]()
由D对a的偏导分析得到:
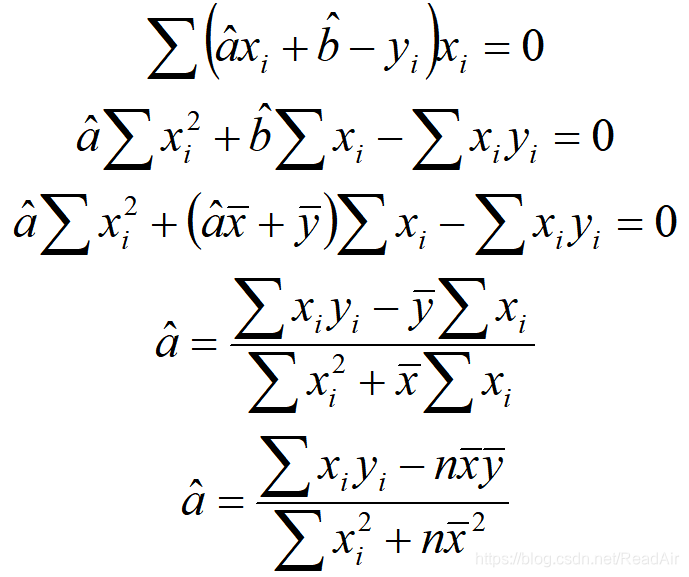
现在大家应该知道最小二乘法的套路了:
- 找到需要拟合的函数
- 构造误差平方和
- 求出拟合函数中各参数的偏导,并使之为0,然后求解等式即可得到参数的最小二乘估计值。
理解了基本原理,我们就可以开始用于各种工程项目中的参数估计和函数拟合啦.
3 抽象
一个优秀的工程师不能只满足会用,我们不妨在做进一步思考:如何把最小二乘写成矩阵形式以适应高阶参数估计呢?当写出了最小二乘法的矩阵形式,是不是意味着我们在线性区域实现了“一招鲜,吃遍天”?
首先掏出一个多元线性函数:
![]()
写成矩阵形式:
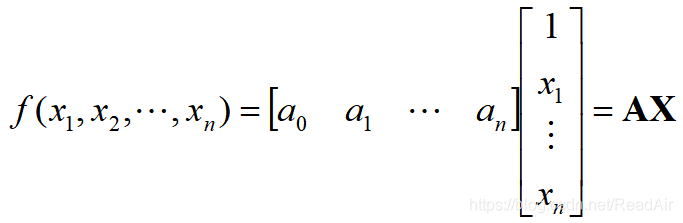
我们的数据是大量的,一共有m组且m>n(m=n时直接求解),我们将其写成矩阵形式:
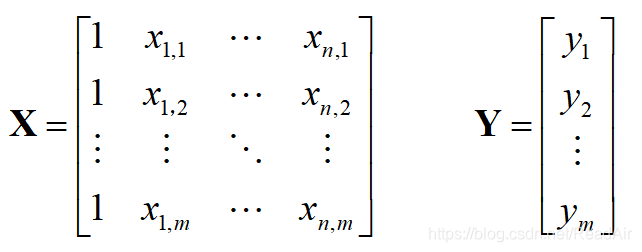
现在矩阵X的尺寸为m*(n+1),矩阵Y的尺寸为m*1,我们是要使用最小二乘法求出公式![]() 中的系数矩阵
中的系数矩阵![]() :
:
我们将误差平方和函数使用矩阵形式表达可得:
![]()
为了将其化简,我们先复习一下和转置相关的矩阵公式:
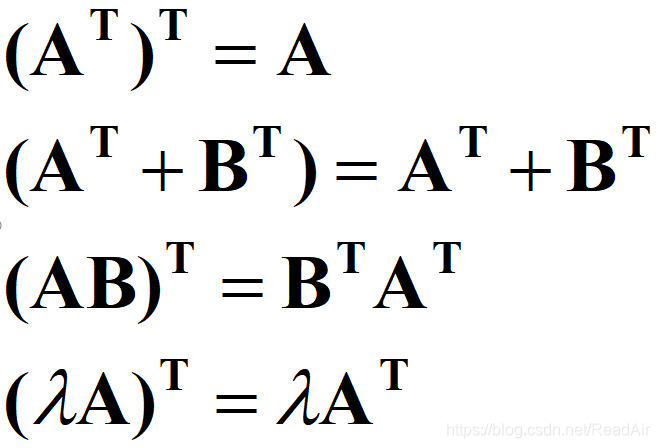
将误差平方和函数展开:
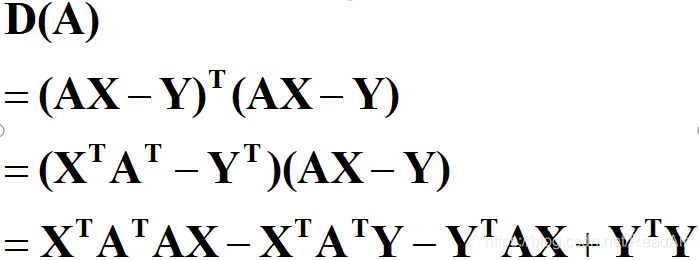
接下来就是对其求偏导并使之等于0矩阵:
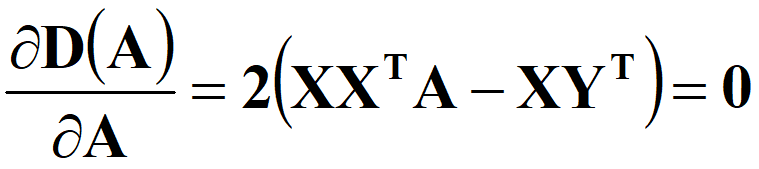
即可得到:
![]()
以上这种写法有些别扭,因为我设置X矩阵为列向量,A矩阵为行向量了,按照书本上主流的写法,X矩阵为行向量,A矩阵为列向量,则公式应写为:
![]()
4 总结
以上就是对最小二乘的介绍。本文只给出了线性回归的一般公式,在遇到非线性函数的拟合时,理论仍然可以使用这种方法做拟合,但是需要对公式做一些变形,这其中有很多tricks,比如对数据进行预处理,使得样本呈线性关系。
综上所述,最小二乘法是一种在拥有充足(冗余)的样本时,对所期望的公式拟合进而得到准确参数的方法。
下一章,我们介绍:卡尔曼滤波