1 卡尔曼滤波(Kalman Filter)简介
卡尔曼滤波是一种基于最优估计的滤波算法,它通过综合考虑估计值和测量值,迭代给出不确定性最小的数值。明白其矩阵形式的公式,就会发现其在数据融合的时候非常方便。
卡尔曼的公式如下,一共5条。读者不要对繁杂的符号产生恐惧,卡尔曼滤波的实质非常简单易懂。
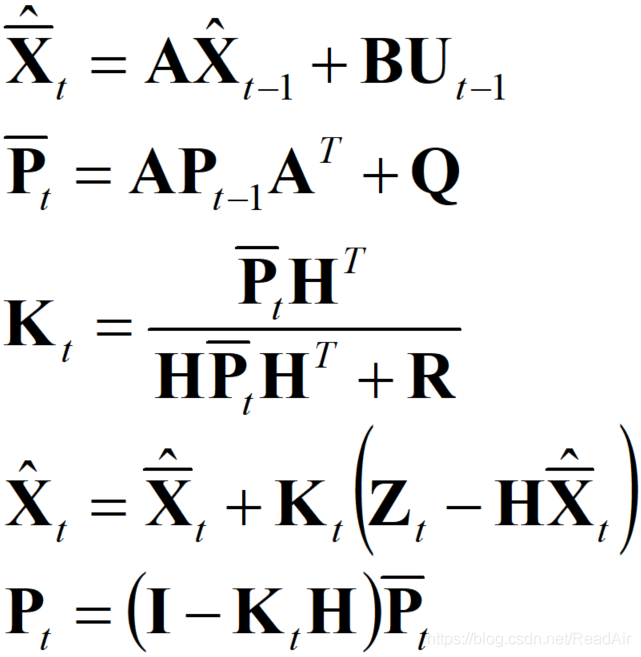
2 公式讲解(逻辑疏导)
写在最前:在下文叙述中:(1)预测值和估计值是一回事,(2)数据的不确定性的大小由数据方差/标准差决定,下面可能混用。
我们先从感性的方向认识一下卡尔曼滤波的思想,卡尔曼滤波的核心思想是:假定观测的系统是线性的,噪声都满足高斯分布。这一刻系统的状态(最优估计)是这一刻的预测值和这一刻的测量值的加权平均,当得到最优估计之后,再将这一刻的最优估计和估计值进行对比,如果相差比较小,则说明估计比较准确,下次计算就加大估计值的权值,否则说明估计值不准确,下次计算就加大测量值的权值。重复以上过程。
让我们换一种说法。测量一个模型的参数时,可以根据过往数据预测下一个数据的走向,我们把这个数值成为预测值,与此同时还有一个传感器可以测量到这个参数。我们称之为测量值,滤波算法呢,给这两个值搞了个五五开:
输出值 = 0.5 * 测量值 + 0.5 * 预测值
如果这个测量值噪声有点大,也就是充满不确定性,怎么办?那就三七开吧,相信预测值多一些:
输出值 = 0.3 * 测量值 + 0.7 * 预测值
咱换一个写法:
输出值 = 0.3 * 测量值 + (1-0.3) * 预测值
= 预测值 + 0.3 *(测量值 - 预测值)
= 预测值 + K *(测量值 - 预测值)
这样我们用一个参数K就可以表示我们对数据的偏好(参数K越大,表示相信测量值越多)。
实际上,估计值和测量值都存在不确定性,所以这个参数的选择是有标准的:希望输出值的不确定性最小。
卡尔曼滤波算法的本质,就是基于数值的不确定性调节这个参数K(卡尔曼增益)。在迭代若干次后逼近输出值不确定性最小的数值。
接下来我们需要解决4个问题:
- 如何获得估计值
- 如何得到估计值的不确定性
- 如何获得卡尔曼增益(参数K)
- 如何完成迭代
注:从下面开始,请关注矩阵的标记:如hat(![]() )和bar(
)和bar(![]() ),其中带有hat标记的表示数据来自预测值,带有bar标记的表示数据是先验的。
),其中带有hat标记的表示数据来自预测值,带有bar标记的表示数据是先验的。
2.1 如何获得估计值
估计,或者叫预测,就是拿过去知道的数据来预测下次的数据,以滑轨上的小车为例,知道上一次的位置x,速度v和加速度a,可以估计下一次的位置在:
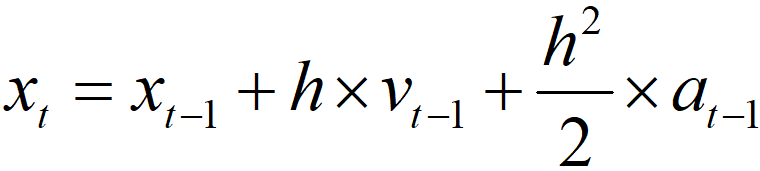
h是步长,也就是时间间隔。为了方便后面公式表达,把它写成状态方程的形式
速度和位置都在状态中:
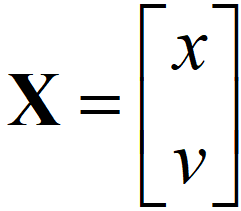
加速度放在控制量矩阵中:
![]()
系数矩阵A:
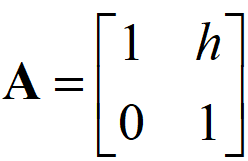
系数矩阵B:
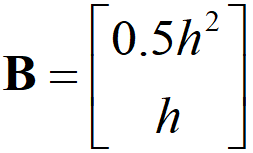
写成矩阵形式:
![]()
观测方程
![]()
Z是测量值,矩阵H是测量值和真实状态之间的关系,对于直接测量的系统,H为单位阵,对于间接测量的系统,则需要H实现映射。比如状态是距离,测量使用的传感器是激光ToF测距传感器(这种传感器通过获得光信号在介质中的传播时间来计算发射位置到反射面的距离),也就是测量了光在二倍距离下传播的时间。那么H矩阵就应该是介质光速倒数的两倍 2c^-1 。
在理想情况下,没有测量噪声,测量值和真实状态是绑定的(原谅我词汇匮乏,意思就是测量值可以反映真实状态,就是理想传感器,仿真里面大家都用过的)
2.2 如何得到估计值的不确定性
现在我们进入了真实环境:无论是估计还是测量,都带有高斯分布的噪声(W和V):

估计噪声 W 和量测噪声 V 满足高斯分布:

Q,R 为估计噪声 W 和量测噪声 V 的方差。
现在要做的就是求出一个参数K,融合先验的状态估计值Xt和测量值Zt,使最终的结果中包含噪声W,V的成分最少。如何衡量数据中噪声成分的多少呢?我们引入了协方差矩阵的概念,对于估计值,协方差矩阵为:
![]()
其中前面一部分:![]() 来自上一次的估计,上一次的数据就有不确定性(噪声),基于上次数据做的预测,必然带有上次的不确定性,此外预测本身就引入了新的噪声,我们认为这是固定的,也就是
来自上一次的估计,上一次的数据就有不确定性(噪声),基于上次数据做的预测,必然带有上次的不确定性,此外预测本身就引入了新的噪声,我们认为这是固定的,也就是![]() 。如此一来,我们就得到了估计值的不确定性。
。如此一来,我们就得到了估计值的不确定性。
再来看测量值的不确定性,也就是观测噪声的方差,是多少呢?一个常数——![]() ,好嘛真开心,遇到一个不要计算的,为啥?传感器得到的数据,误差就是不变的呀,随便找一个传感器,厂家都会在手册上写的清清楚楚:测量误差是多少,这是一个固定的数据。
,好嘛真开心,遇到一个不要计算的,为啥?传感器得到的数据,误差就是不变的呀,随便找一个传感器,厂家都会在手册上写的清清楚楚:测量误差是多少,这是一个固定的数据。
2.3 如何获得卡尔曼增益(参数K)
如此一来,参数K的取值就毫无悬念了:
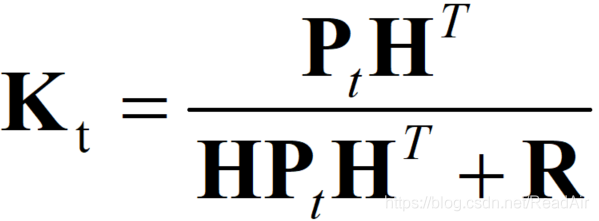
卡尔曼滤波输出的最终状态为:
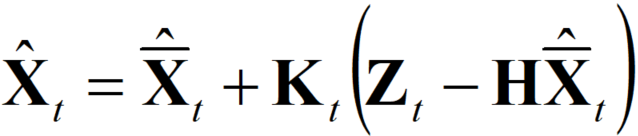
根据以上两个公式可以看到,如果传感器的不确定性为0(仿真中的理想传感器),那么卡尔曼增益参数K将变成单位阵(假设H为单位阵),也就是输出值等于测量值。完全不看估计值了。在假设上次的估计的数值非常准确,给出的不确定度为0(比如触发了某个事件,如电机转动到了触发限位开关的特定角度),那么估计值的不确定性就只有Q,卡尔曼增益K因此下降,使得本次输出更加相信估计值。
2.4 如何完成迭代
最后一步,更新本次输出值的不确定性:
![]()
特别注意![]() 和
和![]() 不一样,P拔(P-bar)的估计值的协方差矩阵(不确定性),P是本次滤波输出值的协方差矩阵(不确定性)。
不一样,P拔(P-bar)的估计值的协方差矩阵(不确定性),P是本次滤波输出值的协方差矩阵(不确定性)。
而本次输出的协方差矩阵(不确定性),就是下一次计算估计值协方差矩阵时使用的“上一次数值的协方差矩阵(不确定性)。如此便完成了迭代
2.5 卡尔曼滤波五步走
现在我把卡尔曼滤波的五个公式一起列出:
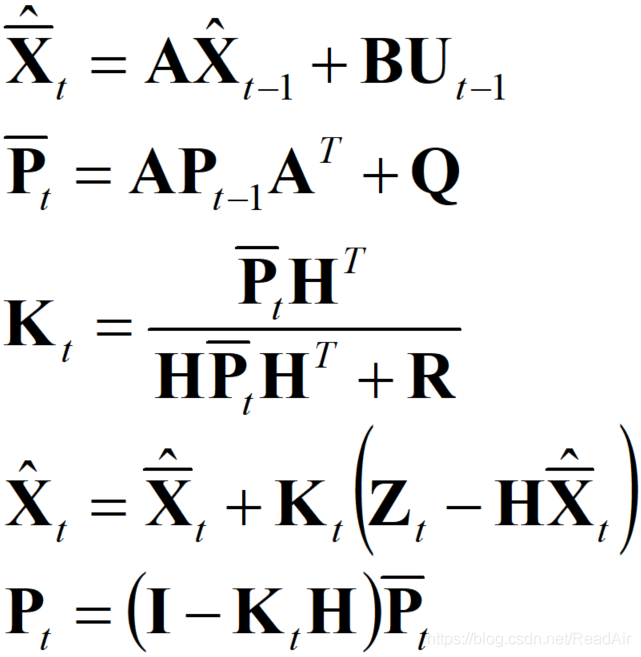
公式1:基于过去时刻的状态以及控制量对当前时刻的状态进行估计,注意,数据是先验的。
公式2:计算公式1的先验估计状态的协方差矩阵,前一部分是由上次最优估计值自身引入的协方差,后一部分是本次估计产生的不确定性(比如无法预测的外部扰动以及模型自身的不确定性)。
公式3:计算卡尔曼增益(参数K),这个参数决定了相信估计值还是相信测量值多一些。
公式4:就是根据公式4的卡尔曼增益计算得到的最优状态估计值
公式5:计算本次最优状态估计值的协方差矩阵,这个数据在下一次迭代的公式2中被用到。
3 公式讲解(数学推导)
对于头一回接触卡尔曼滤波的学习者,看完第二部分的公式一定会满头问号,道理我都懂,为什么公式是这样的呢?这部分我将对卡尔曼滤波的5个公式的产生做数学推导。这部分涉及到了一些线性代数、矩阵论、以及一些基础的微积分知识。
3.1 公式1的推导——先验状态估计
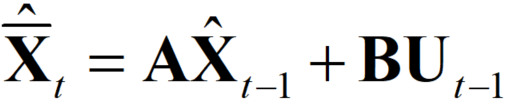
公式1的作用是估计出先验的状态,这个公式的意义非常明显,学过现代控制的都知道这就是状态方程,矩阵A,B分别是状态转移矩阵和控制量转移矩阵。有时候,我们需要做卡尔曼滤波的对象没有控制量输入,那么BU这一项可以省去。有一些博客中认为控制量矩阵U是 t 时刻的,这是不正确的,当前的状态只受到上一时刻状态和上一时刻控制量的影响,在离散的情况下,本次的控制量只能对下一次的状态造成影响。
我继续使用滑轨小车的例子来说明
(公式推导及图片稍后补全)
3.2 公式2的推导——先验估计的不确定性
![]()
这个公式应该是很多人困惑的地方。先验状态估计的协方差矩阵为什么是这么个形式的呢?
首先补充一些关于协方差矩阵的知识:
![]()
解释:两个向量的协方差就是两个向量偏离均值部分乘积的期望,并且由此易得:
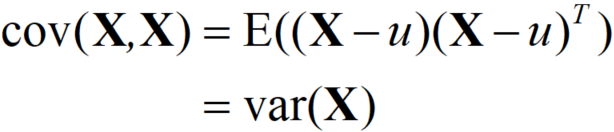
下面开始求先验状态估计的协方差矩阵![]() :
:
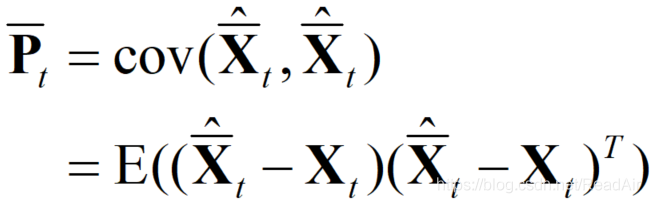
第2行是为什么呢?因为先验估计值的期望就是真值,当然真值是我们不知道的。
有些博客把这个部分叫做先验误差,记做:
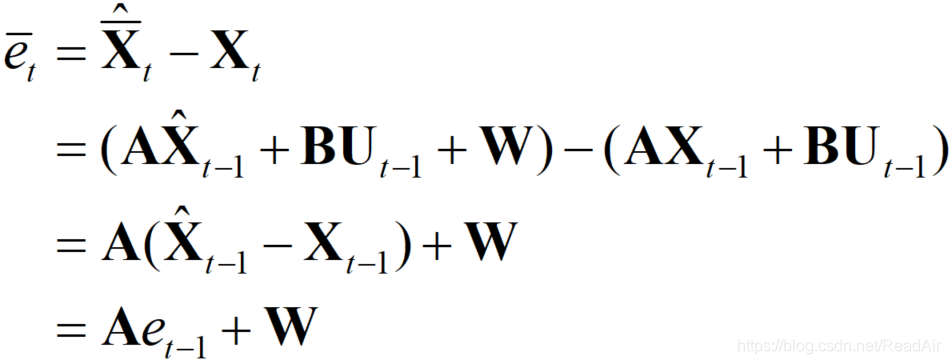
那么先验估计的协方差矩阵可以这样推导:
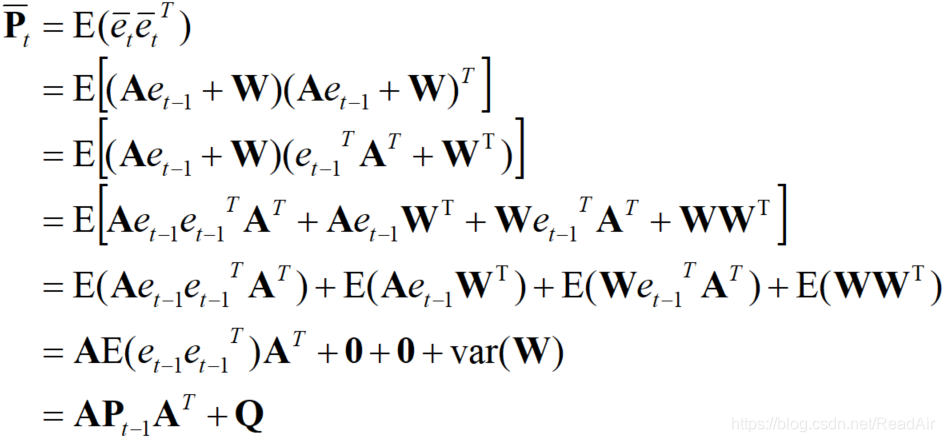
等式第1行:参照前两个公式,我们发现先验估计的协方差实际上就是先验估计误差的方差
等式第2行:把先验估计误差的式子展开备用
等式第3行:把后面一项括号外的转置放到括号内,其中用到的公式有:
![]()
![]()
等式第4行:把式子乘开,变成四项的多项式
等式第5行:展开期望表达式为四项,应用的公式:
![]()
等式第6行:
- 第1项期望中的常数可以提出来,中间部分可以看到是上一时刻的最优估计值的协方差矩阵;
- 第2,3项期望观察可以发现实际可以做上一时刻最优估计值与估计噪声的协方差,而这两项是概率的独立的,显而易见其协方差为0;
- 第4项期望实际就是估计噪声的方差,我们可以根据协方差公式的定义得到。
等式第7行:上一时刻的最优估计值的协方差矩阵就是![]() ,而估计误差的方差是我们给定的
,而估计误差的方差是我们给定的 ![]() 。这样我们就推导出了卡尔曼滤波的第二个公式。这个公式告诉我们先验估计状态的不确定性有多少。
。这样我们就推导出了卡尔曼滤波的第二个公式。这个公式告诉我们先验估计状态的不确定性有多少。
3.3 公式3的推导——卡尔曼增益
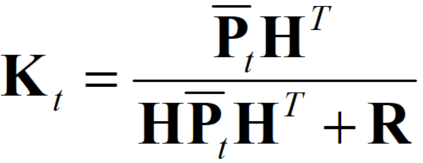
这个公式可以说是卡尔曼滤波的精髓了,首先我们要知道卡尔曼增益的目的是:让融合了先验估计值和测量值的方差在所有Kt的取值中最小。基于这个思想,我们很容易想到使用求导的方式来找到最佳的卡尔曼增益。方差就是协方差矩阵主对角线上的元素。总的方差可以用矩阵的迹(记作![]() ,表示方阵主对角线上元素之和)来表示。
,表示方阵主对角线上元素之和)来表示。
所以要找到满足下列等式的Kt:
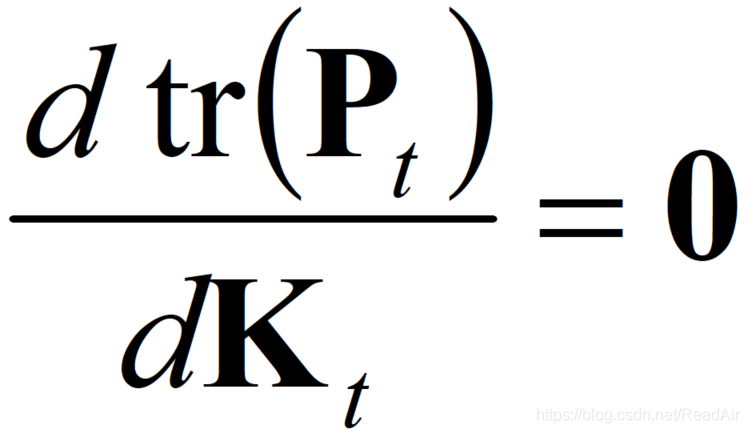
为了求解这个公式,我们需要先写出Pt的表达式:
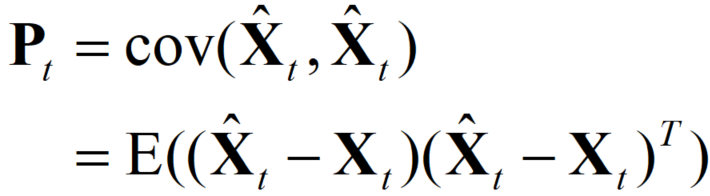
注意到了吗,这个形式和我们求 ![]() 的公式很像,只是去掉了象征先验数据的一横(bar)符号。
的公式很像,只是去掉了象征先验数据的一横(bar)符号。
那我们如法炮制,令后验误差为:
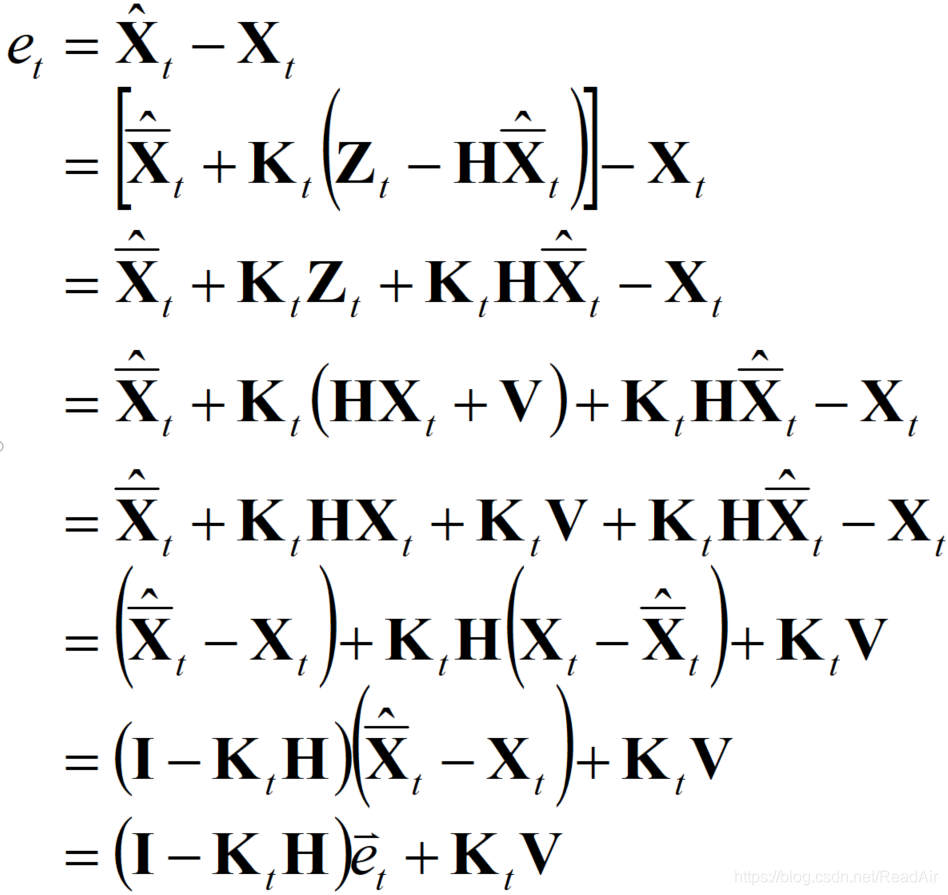
等式第1行:这是后验误差的表达式;
等式第2行:把估计值展开了,也就是卡尔曼公式4(先借来用一下,下一小节我们会讲这个公式);
等式第3行:去掉括号,把所有式子乘开;
等式第4行:把测量值也展开,它是真值(基于真实状态的测量)加上一个0均值高斯分布的测量噪声 V;
等式第5行:去掉括号,把所有式子乘开;
等式第6行:合并了先验估计状态和真值的差,下面为了合并。
等式第7行:继续合并。
等式第8行:用先验估计误差![]() 表示先验估计状态和真值的差。之所以写成这个格式,我们的目的是阐明卡尔曼估计值的误差和先验估计误差的关系。
表示先验估计状态和真值的差。之所以写成这个格式,我们的目的是阐明卡尔曼估计值的误差和先验估计误差的关系。
得到了卡尔曼估计值的误差表达式,可以继续卡尔曼估计值的协方差Pt了:

等式第1行:这是后验协方差的表达式;
等式第2行:把后验误差展开,变成包含先验误差的式子,因为这些的期望是已知的;
等式第3行:后一项转置转移到括号内;
等式第4行:式子乘开,变成4项;
等式第5行:四项和的期望变成4项的期望和,并且把常数放在了外面;
等式第6行:
- 第1项期望中的常数可以提出来,中间部分先验误差的协方差我们是知道的,就是
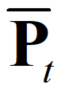 ;
; - 第2,3项期望看到都是先验误差和观测噪声的协方差,而这两项是概率的独立的,显而易见其协方差为0;
- 第4项期望实际就是测量噪声的方差,我们可以根据协方差公式的定义得到;
等式第7行:展开式子;
等式第8行:展开式子。
得到了展开的式子,我们掏出之前的等式开始计算:

等式第1行:卡尔曼输出值的协方差矩阵 Pt 的迹对卡尔曼增益 Kt求导。目的是找到使 tr(Pt) 最小的卡尔曼增益 Kt;
等式第2行:展开 Pt 的表达式
等式第3行:应用了如下公式展开微分项 :
![]()
等式第4行:
- 第1项微分由于先验协方差是常数(对于Kt),所以该项微分为0;
- 第2,3项微分应用了如下公式:
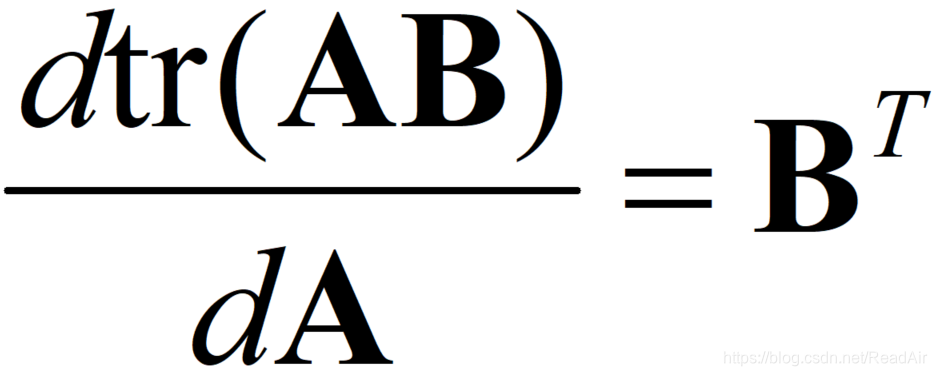
![]()
- 第4,5项微分应用了如下公式:
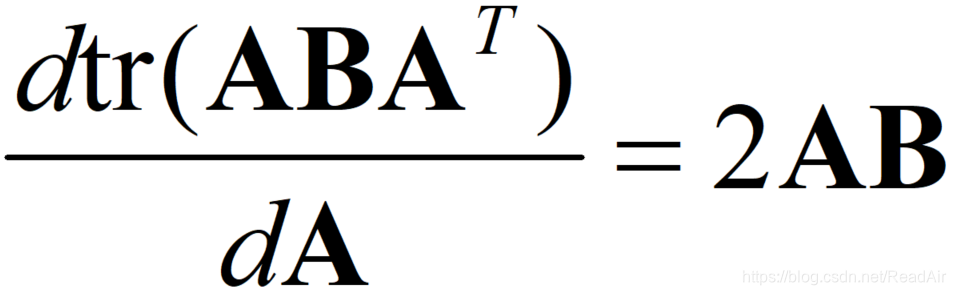
等式第5行:整理同类项并将转置处理至括号内
等式第6行:消除相同系数,注意,由于![]() 是对阵帧,即
是对阵帧,即![]() 的转置即为本身。所以消去了
的转置即为本身。所以消去了![]() 的转置符号
的转置符号
等式第7行:化成分数形式。注意,之所以可以写成分式形式,是因为我们确信上下部分的运算结果都是对角阵,至此我们得到的卡尔曼增益的表达式,也表明在此时,获得的估计值不确定性最小。
3.4 公式4的推导——最优估计值
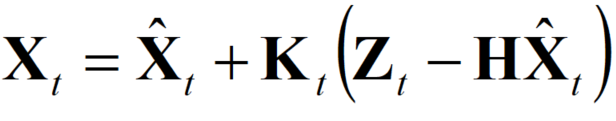
这个公式非常好理解了,在本文第二章的开头已经将这个公式描述的很清楚。这个公式就是根据卡尔曼增益对估计值和观测值做了加权平均。
3.5 公式5的推导——最优估计值的不确定性

这个公式是为了得到此时刻的方差矩阵,这是如何计算的呢?在公式3求卡尔曼增益的时候我们已经列出了卡尔曼估计值的表达式。现在已经得到了最优的卡尔曼增益,我们带入表达式的后三项,发现被消掉了:
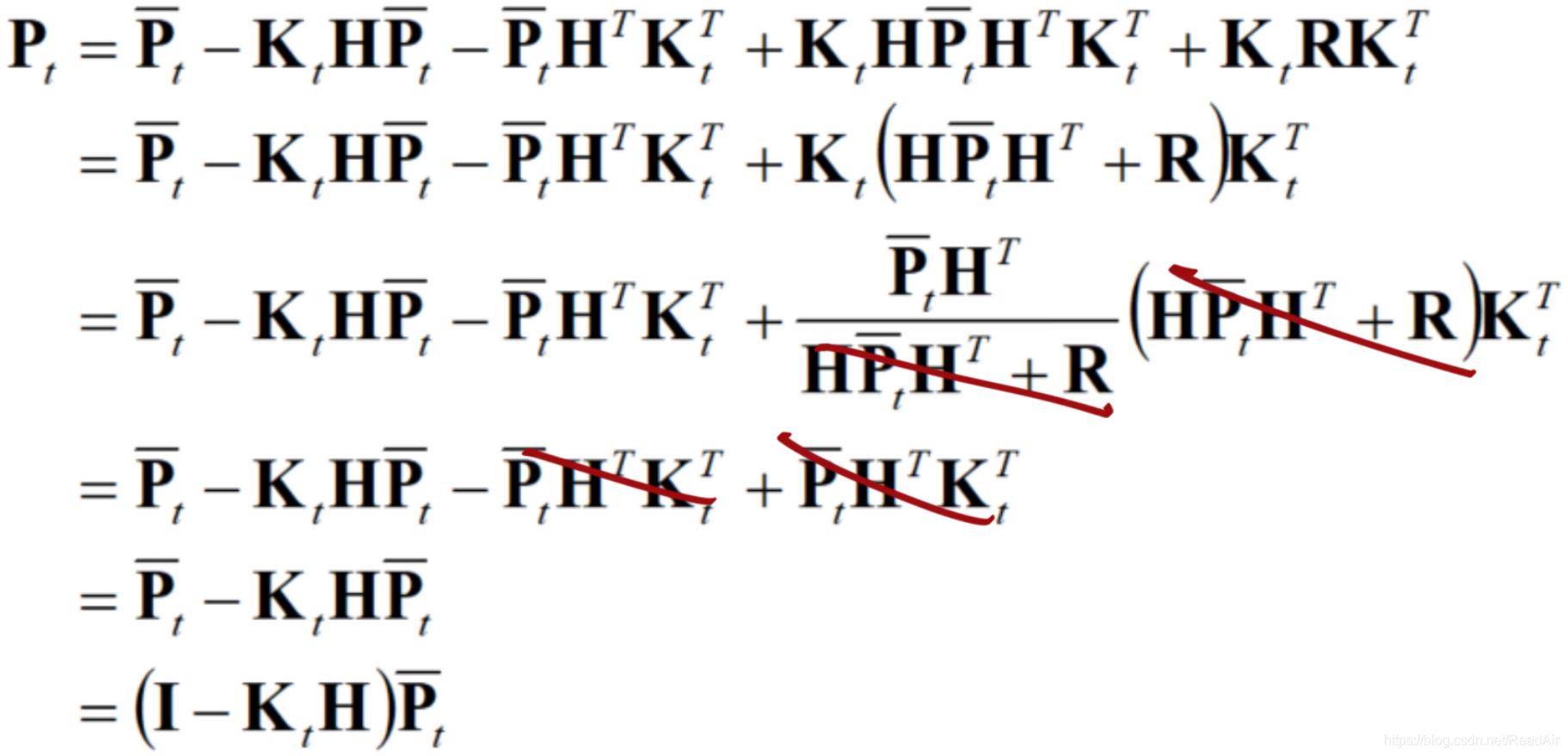
等式第1行:已知的等式,在第三条公式处完成了推导
等式第2行:合并了后两项
等式第3行:将公式3带入第四项的卡尔曼增益kt,抵消了
等式第4行:第3,4项抵消了
等式第5,6行:提出单位阵,变成我们常见的形式。
4 工程应用中的细节
4.1 估计噪声和测量噪声的方差
在实际的工程应用中,这些数值是需要实测,不过我们可以从公式发现,只要固定估计噪声和测量噪声的方差的比值![]() ,计算的结果就是一样的,这是一些高手不愿意说的技巧!实际上,我们在实际测试滤波效果的时候,调整比值
,计算的结果就是一样的,这是一些高手不愿意说的技巧!实际上,我们在实际测试滤波效果的时候,调整比值![]() 就可以改变滤波的效果,这个比值越大,说明测量值越不可靠。
就可以改变滤波的效果,这个比值越大,说明测量值越不可靠。
4.2 矩阵H
在推导公式的时候我们就觉得这个H非常碍眼(我敲公式的时候也是),但是在实际写代码的时候,我们可以认为的把H设为单位矩阵。只要确保传感器的数值是反应直接测量的状态
4.3 初始值
迭代的初始需要提供估计值的初值。为了提高数据的收敛速度,最好把协方差矩阵 Pt 初始值设为非零数,即开始的状态基于测量值(当然,如果你有非常可靠的状态初值,建议把协方差矩阵 Pt 初始值设为零)。
5 Q&A
(补充中)
6 参考资料
在撰写本文过程中,参考了许多资料,包括维基百科、知乎专栏、博客,以及手边的基本数学书。下面列举了一些对我启发特别大并且比较容易理解的资料来源。这些资料中提供的思想和推导过程都写的很好,值得学习借鉴。
6.2 知乎
如何通俗并尽可能详细地解释卡尔曼滤波?——云羽落 的回答:https://www.zhihu.com/question/23971601 搬运并翻译了MATLAB社区的视频。适合入门。
图说卡尔曼滤波,一份通俗易懂的教程——bzarg大佬介绍kalman filter文章的译文:https://zhuanlan.zhihu.com/p/39912633
6.2 博客
卡尔曼滤波详解——无比机智的永哥 的博客:https://blog.csdn.net/honyniu/article/details/88697520 条理很清晰的一篇博文,适合
6.3 Bilibili
UP主DR_CAN的系列视频:
- 【卡尔曼滤波器】1_递归算法_Recursive Processing
- 【卡尔曼滤波器】2_数学基础_数据融合_协方差矩阵_状态空间方程_观测器问题
- 【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ~全网最完整
- 【卡尔曼滤波器】4_误差协方差矩阵数学推导_卡尔曼滤波器的五个公式
下一章我们介绍:(休息一会,这篇写的有点费脑子)